标签:tca 执行时间 .com 阅读 return pos tree 矛盾 body
什么是数据结构?
指数据元素之间的关系。这些关系可以分为:
集合
线性结构
树形结构
网状结构。
逻辑结构分为: 线性结构 和 非线性结构。
集合:除了同属一个对象外不存在相互关系。如:汽车上的人除了同辆车彼此间无其他关系。

线性结构:元素间为严格的一对一关系,即一个元素有且只有一个前驱。如:成绩表中一个学生一个成绩

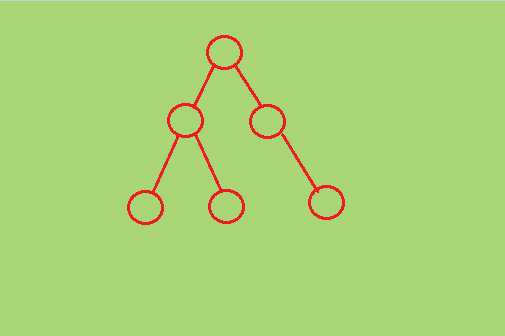
树形结构:元素之间为严格的一对多关系,即一个元素有且只有一个前驱,但可以多个后继。如家谱,行政组织
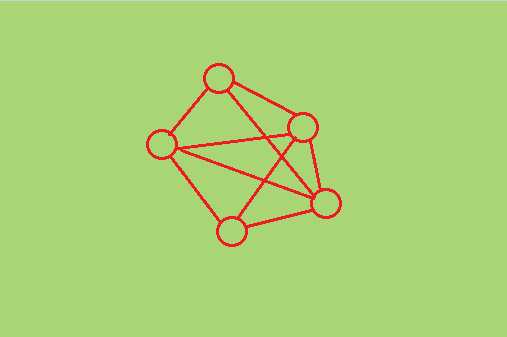
网状结构:元素之间存在多对多的关系,比较复杂。如:微信朋友圈
如何描述数据结构?
使用二元组来描述数据结构
Data_structure = (D,R)
D 是元素的有限集
R 是D上所有元素的关系有限集
下面举一些例子
线性结构可以用二元组表示为:
linear = (D,R)
D = {A,B,C,D,E,F,G,H}
R = {r}
r = {<A,B>,<B,C>,<C,D>,<D,E>,<E,F>,<F,G>,<G,H>}
树形结构可以用二元组表示为:
tree = (D,R)
D = {A,B,C,D,E,F,G,H,I,J}
R = {r}
r = {<A,B>,<A,C>,<A,D>,<B,E>,<B,F>,<C,G>,<C,H>,<C,I>,<D,G>}
网状结构可以用二元组表示为:
nets = (D,R)
D = {1,2,3,4,5}
R = {r}
r = {(1,2),(1,3),(1,4),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)}
尖括号表示有向线,圆括号表示无向线。
将上面的尖括号或圆括号的元素用线连一下便是对应的形状了。
数据结构如何存储?
顺序存储结构:数据元素依次存储在一组连续存储单元当中,数据逻辑关系由存储单元的位置直接体现。
链式存储结构:数据元素存储在任意存储单元当中,而附加的指针域表示元素之间的逻辑关系
程序 = 算法 + 数据结构
数据结构离不开算法,下面说说算法
什么是算法?
算法具有五个特性:
有穷性:一个算法必须在有穷的执行步骤后结束,每步都可以在有穷的时间内完成。
确定性:算法中每条指令必须明确,任何情况下对于相同输入都有相同的输出。
可行性:算法中描述的操作均可以用基本运算的有限执行次数来实现。
输入:一个算法有0个或者多个输入,这些输入是某个特定对象的合集
输出:一个算法至少有一个输出,与输入有着某些特定关系的量。
如何设计算法?
正确性:除了语法正确,逻辑上也正确,能达到预期的目,最好可以验证结果是否正确。
可读性:方便阅读,交流,改进
健壮性:输入非法参数,算法能及时给出错误答案,并输出错误提示,同时终止程序。
效率与存储:执行的时间越短越好,使用的空间越少越好,虽然时间和空间总算矛盾的
算法的时间复杂度
事后统计:将不同的算法编制成程序,然后比较这些程序执行的时间。
事前估算:用数学方法对算法效率直接分析,常用此方法来判断时间复杂度。
事前估算需要考虑的因数:
1.问题的规模,排序10个数字比排序100个数字时间短
2.编写的语言,越高级的语言执行的效率越低。
3.机器的速度,80386和i7的速度没得比
4.算法本身的策略。
由于2,3因数需要考虑到硬件,软件(编译器)等因数,因此用绝对的机器运行时间来衡量算法
是不科学的,所以需要抛开这些因数,主要研究时间效率与算法所处理的问题规模n的函数关系
当随着问题规模n增大时,算法执行时间的增长率与f(n)的增长率相同,称为算法的渐进时间复杂度。记作:
T(n) = O(f(n))
执行时间 == 执行次数(假设执行一条语句所用的时间相同),另外下面的时间复杂度都以最坏的情况考虑
下面是常见的时间复杂度:
常数阶 O(1)
对数阶 O(logn)
线性阶 O(n)
平方阶 O(n^2)
立方阶 O(n^3)
指数阶 O(2^n)
阶数阶 O(n!)
爆炸阶 O(n^n)
下面两段代码是累加求和
1 int sum1(){
2 int i,sum=0,n=100; #执行了1次
3 for(i=0;i<n;i++) #执行了n+1次
4 sum += i; #执行了n次
5 }
高斯算法
1 int sum2(){
2 int n,sum=0; #执行了1次
3 sum = n(n+1)/2; #执行了1次
4 }
上面两段代码中 n 是问题的规模。
第一个算法执行次数为:1 + n+1 + n = 2n+2
随着问题规模n的增加,执行次数以线性增加,所以时间复杂度为O(n)
第二个算法执行次数为:1 + 1 = 2
随着问题规模n的增加,执行次数始终为2,所以时间复杂度为O(1)
所以时间复杂度计算规则为:
1.如果执行的次数是常数,与规模n无关,则为O(1)
2.如果执行的次数是多次多项式,取最高项,如:n^3 + n^2 则为O(n^3)
3.如果执行的次数是含有系数和常数,可以忽略系数和常数,如: 2n^2 + 3 则为O(n^2)
有了上面的法则,来分析下下面这些算法的时间复杂度,n均代表问题规模。
1 #define n 10
2 int multiMatrix(int a[n][n],b[n][n],c[n][n]){
3 for(i=0;i<=n;i++) #执行了n+1次
4 for(j=0;j<n;j++){ #执行了(n+1)*n次
5 c[i][j] = 0; #执行了n^2
6 for(k=0;k<n;k++) #执行了n^2*(n+1)次
7 c[i][j] = c[i][j] +a[i][k] * b[k][i]; #执行了n^3
8
9 }
10 }
T(n) = 2n^3 + 3n^2 + 2n + 1 所以时间复杂度为O(n^3)
1 int fun(){
2 i=1;n=100;
3 while(i<n){
4 i = i * 2;
5 }
6 }
假设上面的算法执行了x次后停止。则有 2^x >= n,所以 x = log(2)n,所以时间复杂度为O(logn)
1 void prime(n){
2 i=2;
3 while( (n%i)!=0 && i*1.0<sqrt(n) ) #如果不能被整除,且小于根号n,则继续执行
4 i++;
5
6 if(i*1.0>sqrt(n))
7 printf("%d是个素数\n",n);
8 else
9 printf("%d不是素数\n",n);
10
11 }
函数作用判断n是否为素数,原理就是遍历开区间(1,n)间的数,然后看看遍历的数能否被整除。
事实上如果 n^1/2 (根号n)前不存在一个数能被n整除,那么n^1/2(根号n)之后的数也不会被n整除
这是因为对称性。因此只需要判断 n^1/2(根号n)之前的数字是否存在一个能被n整除的数即可。
所以随着问题规模n的增加,执行的次数增长率与 f(n)=n^1/2 的渐进增长率相同,所以T(n)=O(n^1/2)
后面还有几道具有挑战的题目,这里先讲讲空间复杂度:
算法的空间复杂度
指算法对运算所需要的辅助工作单元和存储为实现计算所需信息辅助性的空间大小,记作:
S(n) = O(f(n));
这个大小不包括输入数据占用的空间,大小是由具体的实际问题来决定的。
下面一个例子:判断三个数字中,哪个数最大
1 max(int a,b,c){
2 if(a>b){
3 if(a>c)return a;
4 else return c;
5 }
6 else{
7 if(b>c)return b;
8 else return c;
9 }
10 }
随着问题规模增大,执行的次数也增大,时间复杂度为O(n)
1 max(int a[3]){
2 c=a[0];
3 for(i=0;i<3;i++)
4 if(a[i]>c)c=a[i];
5
6 return c;
7 }
随着问题规模增大,执行的次数也增大,时间复杂度也为O(n)
上面两个例子时间复杂度相同都为O(n),但第一个算法无需额外的空间,而第二个算法需要两个变量辅助。
所以第一个算法空间复杂度优于第二个算法,但是当问题规模不是3 而是100的时候,相信没人会用第一个
算法,因为会写到手残。
欢迎各位转载,请指明出处:http://www.cnblogs.com/demonxian3/p/7075441.html
最后来几个练习题,评论附上答案
选择题
1 int fun(int n){
2 i=1,s=1;
3 while(s<n)
4 s += ++i;
5
6 return i;
7 }
A. O(n/2) B. O(logn) C. O(n) D.O(n^1/2)
for(int i=0;i<m;i++)
for(int j=0;j<n;i++)
a[i][j] = i*j;
A. O(m^3) B. O(n^2) C. O(m*n) D.O(m+n)
计算题,设n为整数求下面的时间复杂度
(1)
1 i=1,j=0; 2 while(i+j<n) 3 if(i>j) j=j+1; 4 else i=i+1;
(2)
1 x=91,y=100;
2 while(y>0)
3 if(x>100){
4 x=x-10;
5 y=y-1;
6 }
7 else
8 x=x+1;
(3)
1 x=n 2 while(x>=(y+1)*(y+1)) 3 y=y+1;
标签:tca 执行时间 .com 阅读 return pos tree 矛盾 body
原文地址:http://www.cnblogs.com/Leo_wl/p/7095829.html