标签：res height 使用 trim cli 实现 个数 void start
快速排序
排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。
快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。
算法步骤：
1 从数列中挑出一个元素，称为 “基准”（pivot），一般选择第一个
2 从后查找比pivort小的数， 从前查找比pivort大的数， 交换两个数的位置， 直到前后两个指针相遇，交换pivort 和当前指针的值
3 递归地（recursive）把小于pivoirt元素下标的子数列和大于pivort元素下标的子数列排序。
以下选第一个元素为pivort，查找第一个元素的位置 （详细内容：http://developer.51cto.com/art/201403/430986.htm）
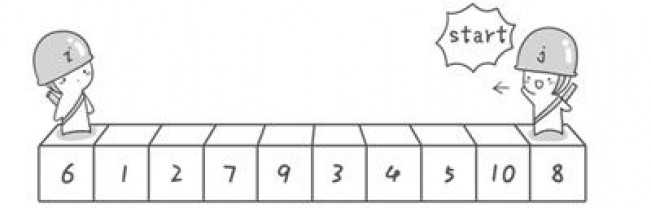
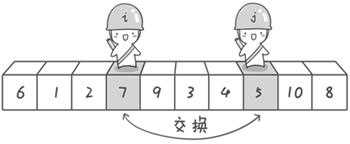
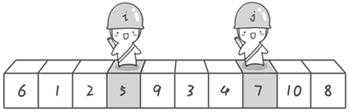
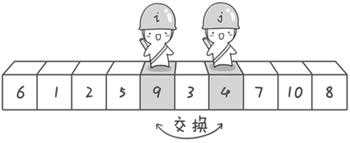j > i 两者交换
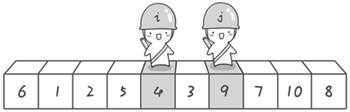
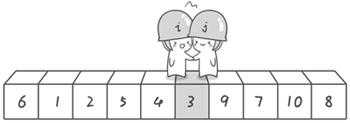j == i 与pivort(0)交换
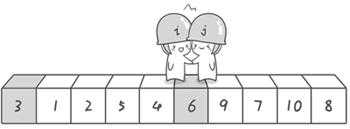
private void QKSort_Click(object sender, EventArgs e) { Result.Text = ""; //Result 是Form 端的一个TextBox int[] values = { 6, 1, 2, 7, 9, 3, 4, 5, 10, 8 ,6,6,0}; QKSort_Part(values, 0 , values.Length-1); for(int i =0; i< values.Length; i++) { Result.Text = Result.Text + "," + values[i]; } Result.Text = Result.Text.TrimStart(‘,‘); } private void QKSort_Part(int[] values, int from, int to) { int i = from; int j = to; if (to <= from) { return; //递归退出条件 } while (true) { var pivort = values[from]; while (values[j] >= pivort && j > i) { j--; } while (values[i] <= pivort && j > i) { i++; } if (j > i) { values[i] = values[i] + values[j]; values[j] = values[i] - values[j]; values[i] = values[i] - values[j]; } if (j == i) { values[from] = values[j]; values[j] = pivort; break; } } QKSort_Part(values, from, j - 1); QKSort_Part(values, j + 1, to); }
标签：res height 使用 trim cli 实现 个数 void start
原文地址：http://www.cnblogs.com/pangxiaohai/p/7111055.html
