三维空间两直线/线段最短距离、线段计算算法 【转】

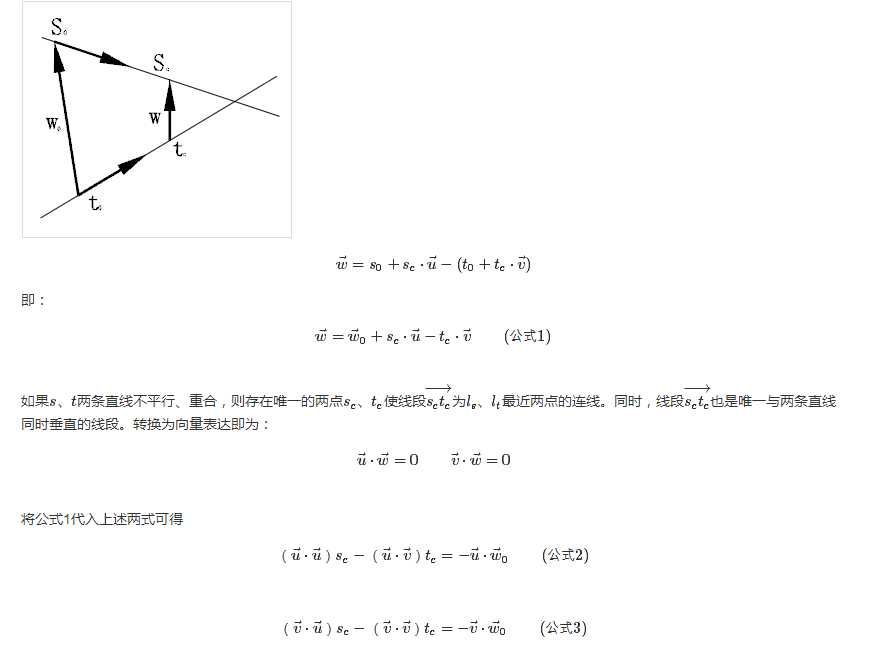
具体实现代码如下（C#实现）：

public bool IsEqual(double d1, double d2)
{
    if (Math.Abs(d1 - d2) < 1e-7)
        return true;
    return false;
}
        
public double SqureDistanceSegmentToSegment(double x1, double y1, double z1,
                                            double x2, double y2, double z2,
                                            double x3, double y3, double z3,
                                            double x4, double y4, double z4)
{
    // 解析几何通用解法，可以求出点的位置，判断点是否在线段上
    // 算法描述：设两条无限长度直线s、t,起点为s0、t0，方向向量为u、v
    // 最短直线两点：在s1上为s0+sc*u，在t上的为t0+tc*v
    // 记向量w为(s0+sc*u)-(t0+tc*v),记向量w0=s0-t0
    // 记a=u*u，b=u*v，c=v*v，d=u*w0，e=v*w0——(a)；
    // 由于u*w=、v*w=0，将w=-tc*v+w0+sc*u带入前两式得：
    // (u*u)*sc - (u*v)*tc = -u*w0  (公式2)
    // (v*u)*sc - (v*v)*tc = -v*w0  (公式3)
    // 再将前式(a)带入可得sc=(be-cd)/(ac-b2)、tc=(ae-bd)/(ac-b2)——（b）
    // 注意到ac-b2=|u|2|v|2-(|u||v|cosq)2=(|u||v|sinq)2不小于0
    // 所以可以根据公式（b）判断sc、tc符号和sc、tc与1的关系即可分辨最近点是否在线段内
    // 当ac-b2=0时，(公式2)(公式3)独立，表示两条直线平行。可令sc=0单独解出tc
    // 最终距离d（L1、L2）=|（P0-Q0)+[(be-cd)*u-(ae-bd)v]/(ac-b2)|
    double ux = x2 - x1;
    double uy = y2 - y1;
    double uz = z2 - z1;

    double vx = x4 - x3;
    double vy = y4 - y3;
    double vz = z4 - z3;

    double wx = x1 - x3;
    double wy = y1 - y3;
    double wz = z1 - z3;

    double a = (ux * ux + uy * uy + uz * uz); //u*u
    double b = (ux * vx + uy * vy + uz * vz); //u*v
    double c = (vx * vx + vy * vy + vz * vz); //v*v
    double d = (ux * wx + uy * wy + uz * wz); //u*w 
    double e = (vx * wx + vy * wy + vz * wz); //v*w
    double dt = a * c - b * b;

    double sd = dt;
    double td = dt;

    double sn = 0.0;//sn = be-cd
    double tn = 0.0;//tn = ae-bd

    if (IsEqual(dt, 0.0))
    {
        //两直线平行
        sn = 0.0;    //在s上指定取s0
        sd = 1.00;   //防止计算时除0错误

        tn = e;      //按(公式3)求tc
        td = c;
    }
    else
    {
        sn = (b * e - c * d);
        tn = (a * e - b * d);
        if (sn < 0.0)
        {
            //最近点在s起点以外，同平行条件
            sn = 0.0;
            tn = e;
            td = c;
        }
        else if (sn > sd)
        {
            //最近点在s终点以外(即sc>1,则取sc=1)
            sn = sd;
            tn = e + b; //按(公式3)计算
            td = c;
        }
    }
    if (tn < 0.0)
    {
        //最近点在t起点以外
        tn = 0.0;
        if (-d < 0.0) //按(公式2)计算，如果等号右边小于0，则sc也小于零，取sc=0
            sn = 0.0;
        else if (-d > a) //按(公式2)计算，如果sc大于1，取sc=1
            sn = sd;
        else
        {
            sn = -d;
            sd = a;
        }
    }
    else if (tn > td)
    {
        tn = td;
        if ((-d + b) < 0.0)
            sn = 0.0;
        else if ((-d + b) > a)
            sn = sd;
        else
        {
            sn = (-d + b);
            sd = a;
        }
    }

    double sc = 0.0;
    double tc = 0.0;

    if (IsEqual(sn, 0.0))
        sc = 0.0;
    else
        sc = sn / sd;

    if (IsEqual(tn, 0.0))
        tc = 0.0;
    else
        tc = tn / td;

    double dx = wx + (sc * ux) - (tc * vx);
    double dy = wy + (sc * uy) - (tc * vy);
    double dz = wz + (sc * uz) - (tc * vz);
    return dx * dx + dy * dy + dz * dz;
}

参考文献：http://geomalgorithms.com/a07-_distance.html