循序渐进学数据结构（算法）

标签：height   strong   ++   依据   class   多少   算法   tab   font   

1.算法

是解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

2.算法的比较

下面是一个栗子：求和的算法比较。

//普遍求和
int i, sum = 0, n = 100;
for (i = 1; i <= n; i++)
{
    sum += i;
}
MessageBox.Show(sum.ToString());

//高斯求和
int sum = 0, n = 100;
sum = (1 + n) * n / 2;
MessageBox.Show(sum.ToString());

可以很明显的看出，第一种方法for循环内部执行了n次，第二种方法只执行了1次。

可能n为100，两者之间性能差异很小，如果是10000000000000000000000000000000这样呢？结果可想而知。

3.算法的特性

1. 输入输出：零个或多个输入，一个或多个输出；
2. 有穷性：会自动结束而不会无限循环；
3. 确定性：每一步都有确定的含义，不会出现不二性；
4. 可行性：每一步都必须可行，执行有限次数完成。

4.算法设计的要求

1. 正确性
   • 算法程序没有语法错误
   • 算法程序对于合法的输入数据能够产生满足要求的输出结果。
   • 算法程序对于非法的输入数据能够得出满足规格说明的结果。
   • 算法程序对于精心选择的，甚至刁难的测试数据都有满足要求的输出结果。
2. 可读性：算法设计的另一个目的是为了便于阅读、理解和交流
3. 健壮性：当输入数据不合法时，算法也能做出相关处理，而不是产生异常或莫名其妙的结果
4. 时间效率高和存储量低

• • 效率：对于同一个问题，如果有多个算法可以解决，执行时间短的算法效率高，执行时间长的效率低。
  • 存储量：存储量需求指的是算法在执行的过程中需要的最大存储空间，主要指算法程序运行时所占用的内存或外部硬盘存储空间。

5.算法效率的度量方法

1. 事后统计方法：通过设计好的测试程序和数据，利用 计算机计数器对不同算法编制的程序的运行时间进行比较，从而确定算法效率的高低。（缺陷多，不予考虑）
2. 事前分析估算方法:在计算机程序编制之前，依据统计方法对算法进行估算。

　　一个高级程序设计语言编写的程序在计算机上运行所消耗的时间取决于下列因素：

1. 算法采用的策略、方法（根本）
2. 编译产生的代码质量（软件）
3. 问题的输入规模（即输入量的多少）
4. 机器执行指令的速度（硬件性能）

　　分析一个算法的运行时间，要将基本操作数量与输入规模关联起来

　　比如上面的例子，第一种方法两者是线性的规模为n，操作数量为n，第二种方法无论规模n为何值，操作数量都为1，若再此基础上加上一个双层循环，操作数量为n的平方，他们的关系如下图所示：

6.函数的渐进增长

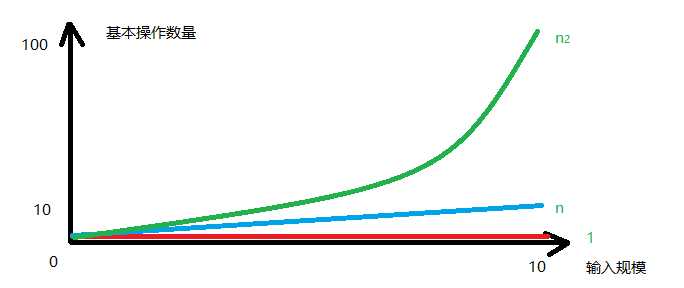
　　给定f(n),g(n),若存在一个整数N，使得所有的n>N,f(n)总大于g(n)，则称f(n)的渐进增长快于g(n)；

　　举个栗子：

　　当n趋近于无限大的时候，我们可以认识到有些数值不会影响我们最终的判断，可以省略

1. 可以忽略加法常熟
2. 可以忽略与最高次项相乘的常数

　　我们主要关注的事最高阶项的阶数，指数越大，增长越快。

7.算法的时间复杂度　

　　T(n)=O(f(n))表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐进时间复杂度，简称时间复杂度。其中f(n)是问题规模n的某个函数。（大O记法）。

　　一般情况下，随着n的增大，T（n）增长最慢的算法为最优算法。

　　O(1)叫常数阶、O(n)叫线性阶、O(n2)叫平方阶。

推导大O阶方法（如何分析算法的时间复杂度）

　　1、用常数1取代运行时间中的所有加法常数。

　　2、在修改后的运行次数函数中，只保留最高阶项。

　　3、如果最高阶项存在且不是1，则去除与这个项相乘的常数。

　　举个栗子：

　　　　3n3+2n2+n+10 => O(n3+1)

　　　　log2n => O(logn)

　　常用的时间复杂度所耗费的时间从小到大依次是：

　　O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)<O(n^n)

8.算法空间复杂度

　　S(n)=O(f(n))   n为问题的规模，f(n)为语句关于n所占存储空间的函数

循序渐进学数据结构（算法）

标签：height   strong   ++   依据   class   多少   算法   tab   font   

原文地址：http://www.cnblogs.com/zysofts/p/7196095.html