二叉树及其数组实现

标签：数组下标   bsp   时间   二叉树的高度   深度   width   时间复杂度   复杂度   个数   

正文如下：

定义：

　　二叉树：

　　　　二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子，左边的叫做左儿子，右边的叫做右儿子，或者说每个结点最多有两棵子树。更加严格的递归定义是：二叉树要么为空，要么由根结点、左子树和右子树组成，而左子树和右子树分别是一棵二叉树。 下面这棵树就是一棵二叉树。

　　概念图：　　

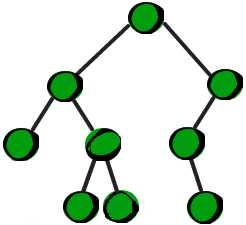
　　深度(高度)：

　　　　这里引入深度的概念，我们规定根结点的深度为1，则其子结点的深度为2，子结点的子结点的深度为3......依次类推。

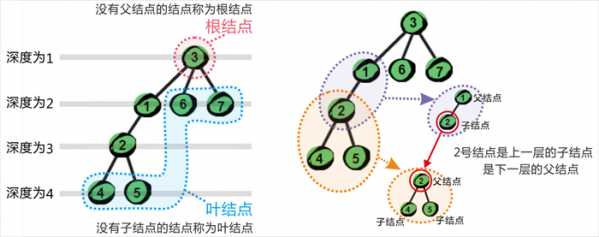
　　二叉树的两种类型：

　　　　1.满二叉树：一颗深度为h且有(2^h)-1个结点的二叉树

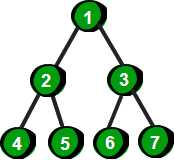
　　　　2.完全二叉树：设高度为h的一棵树，除了第h层外，其他第2~(h-1)层都达到最大结点数，第h层从右向左缺失若干个结点，那么这棵树为完全二叉树。我们可以认为满二叉树为完美的完全二叉树

　　　　如下是完全二叉树的几个例子：

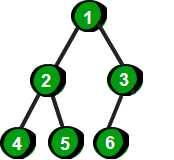
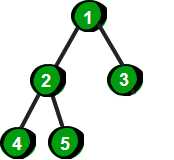
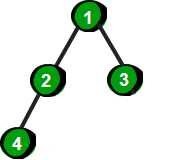
数组实现：

　　概念图：

　　法一：

　　给定一个数组a[n]，若父结点为a[k]，则其左子结点为a[2k]，右子结点为a[2k+1]，左子结点的左子结点为a[(2^2)*k]，左子结点的右子结点为a[(2^2)*k+1]，右子结点的左子结点为a[(2^2)*k+2]，右子结点的右子结点为a[(2^2)*k+3]......

　　可以推导出，深度为n的第一个结点的左子结点(位于n+1层)为a[(2^n)*k]，另一个子结点即右子结点为a[2^n)*k+1]

　　那么我们要求出深度为n+1时的任一结点，只要将其数组下标与深度的关系得出即可列出一个等式，令返回值==等式值即可，时间复杂度为O(1)

　　法二：

　　通过上图我们发现如果完全二叉树的一个父结点编号为k，那么它左儿子的编号就是2*k，右儿子的编号就是2*k+1。如果已知儿子（左儿子或右儿子）的编号是x，那么它父结点的编号就是x/2，注意这里只取商的整数部分。在C语言中如果除号‘/’两边都是整数的话，那么商也只有整数部分（即自动向下取整），即4/2和5/2都是2。另外如果一棵完全二叉树有N个结点，那么这个完全二叉树的高度为log₂ N简写为log N，即最多有log N层结点。

　　　占个坑，待我把二叉树用数组实现后，会在这里贴源码

二叉树及其数组实现

标签：数组下标   bsp   时间   二叉树的高度   深度   width   时间复杂度   复杂度   个数   

原文地址：http://www.cnblogs.com/Bw98blogs/p/7199812.html