标签:span sizeof 包含 idt == 思路 print 更新 算法
【原创】tarjan算法初步(强连通子图缩点)
tarjan算法的思路不是一般的绕!!(不过既然是求强连通子图这样的回路也就可以稍微原谅了。。)
但是研究tarjan之前总得知道强连通分量是什么吧。。
上百度查查:
有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
看不懂。。那么——

看这张图
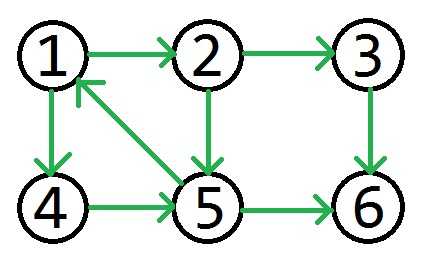
其中从1可以到2,3,4,5,6;
从2可以到1,3,4,5,6;
从3可以到6;
从4可以到1,2,3,5,6;
从5可以到1,2,3,4,6;
从6哪儿都到不了。
我们发现,{1,2,4,5}两两可以互达,我们称其为原图的一个强连通子图,而{3},{6}各自单独为原图的另外两个强连通子图。
我们想要通过程序实现O(n)求所有强连通子图,就要用到tarjan算法。
程序代码如下(tarjan的主要思路写在程序注释里):
1 // Tarjan有向图强连通缩点 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<iostream> 6 #include<string> 7 #define MAXV 10010 8 #define MAXE 100010 9 using namespace std; 10 struct tEdge{ 11 int np; 12 tEdge *next; 13 }E[MAXE],*V[MAXV]; 14 int tope=-1; 15 int n,m; 16 int dfn[MAXV],dfstime=0; // dfn[i]表示点i的dfs序 17 int low[MAXV]; // low[i]表示目前点i所能到达的最小dfs序点 18 int status[MAXV]; // status[i]表示点i的访问状态,0=未访问,1=访问中,2=访问完毕 19 int stack[MAXV],tops=-1; 20 int color[MAXV],totc=0; // color[]表示缩点后的块 21 void addedge(int u,int v){ 22 E[++tope].np=v; 23 E[tope].next=V[u]; 24 V[u]=&E[tope]; 25 } 26 void tarjan(int now){ 27 stack[++tops]=now; // 进栈 28 low[now]=dfn[now]=++dfstime; // 初始化dfs序 29 status[now]=1; // 访问中(在栈中) 30 for(tEdge *ne=V[now];ne;ne=ne->next){ 31 if(status[ne->np]==0){ // 未访问(没有进过栈) 32 tarjan(ne->np); // dfs往下进行递归访问 33 low[now]=min(low[now],low[ne->np]); 34 // 由于now可达ne->np,故ne->np可达的最小dfs序点从now也可达 35 } 36 else if(status[ne->np]==1){ // 回边,发现ne->np为栈中元素 37 low[now]=min(low[now],dfn[ne->np]); 38 // 若ne->np的dfs序比原来now可达的最小dfs序还小则更新 39 } 40 } 41 if(low[now]==dfn[now]){ 42 // now到达的最小dfs序为自己dfs序 43 // 即now不包含在最小dfs序更小的缩点中 44 // 而栈中now以后的节点若不能到达now则早已出栈(FILO) 45 totc++; // 申请新颜色(一种颜色代表一个缩点) 46 while(stack[tops+1]!=now){ // 栈中所有在now之后的节点都在该缩点内 47 status[stack[tops]]=2; // 访问完毕(已出栈) 48 color[stack[tops--]]=totc; // 为节点染色 49 } 50 } 51 } 52 int main(){ 53 memset(dfn,0,sizeof(dfn)); 54 memset(low,0,sizeof(low)); 55 memset(status,0,sizeof(status)); 56 scanf("%d%d",&n,&m); 57 for(int i=1;i<=m;i++){ 58 int u,v; 59 scanf("%d%d",&u,&v); 60 addedge(u,v); 61 } 62 for(int i=1;i<=n;i++) 63 if(status[i]==0) 64 tarjan(i); // 图不连通时必须保证每个点都处理到 65 for(int i=1;i<=n;i++) 66 printf("Point %d colored %d\n",i,color[i]); // 输出所属强连通块编号 67 return 0; 68 }
测试数据:
6 8 1 2 2 3 3 6 5 6 1 4 5 1 4 5 2 5
运行结果:
Point 1 colored 3 Point 2 colored 3 Point 3 colored 2 Point 4 colored 3 Point 5 colored 3 Point 6 colored 1
即color[1]={6},color[2]={3},color[3]={1,2,4,5}为原图的3个强连通子图的缩点。
标签:span sizeof 包含 idt == 思路 print 更新 算法
原文地址:http://www.cnblogs.com/darkleafin/p/7219537.html