标签:jpg img lock euc label 介绍 计算 选择 技术分享
如图所看到的。数据样本用圆点表示,每一个簇的中心点用叉叉表示。(a)刚開始时是原始数据。杂乱无章,没有label,看起来都一样。都是绿色的。
(b)如果数据集能够分为两类。令K=2。随机在坐标上选两个点,作为两个类的中心点。(c-f)演示了聚类的两种迭代。先划分,把每一个数据样本划分到近期的中心点那一簇;划分完后,更新每一个簇的中心。即把该簇的全部数据点的坐标加起来去平均值。这样不断进行”划分—更新—划分—更新”,直到每一个簇的中心不在移动为止。
该算法过程比較简单,但有些东西我们还是须要关注一下。此处。我想说一下"求点中心的算法"
一般来说。求点群中心点的算法你能够非常简的使用各个点的X/Y坐标的平均值。也能够用另三个求中心点的的公式:
1)Minkowski Distance 公式 —— λ 能够任意取值。能够是负数,也能够是正数,或是无穷大。
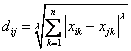
2)Euclidean Distance 公式 —— 也就是第一个公式 λ=2 的情况
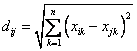
3)CityBlock Distance 公式 —— 也就是第一个公式 λ=1 的情况
![]()
这三个公式的求中心点有一些不一样的地方,我们看下图(对于第一个 λ 在 0-1之间)。



(1)Minkowski Distance (2)Euclidean Distance (3)CityBlock Distance
上面这几个图的大意是他们是怎么个逼近中心的,第一个图以星形的方式。第二个图以同心圆的方式,第三个图以菱形的方式。
Kmeans算法的缺陷
(能够使用Kmeans++算法来解决)
这个算法的实现是。先取一个能落在Sum(D(x))中的随机值Random。然后用Random -= D(x),直到其<=0。此时的点就是下一个“种子点”。
能够看到算法的第三步选取新中心的方法,这样就能保证距离D(x)较大的点,会被选出来作为聚类中心了。
至于为什么原因比較简单,例如以下图 所看到的:

如果A、B、C、D的D(x)如上图所看到的,当算法取值Sum(D(x))*random时,该值会以较大的概率落入D(x)较大的区间内,所以相应的点会以较大的概率被选中作为新的聚类中心。

KNN的算法过程是是这种:
从上图中我们能够看到。图中的数据集是良好的数据。即都打好了label,一类是蓝色的正方形,一类是红色的三角形,那个绿色的圆形是我们待分类的数据。
假设K=3,那么离绿色点近期的有2个红色三角形和1个蓝色的正方形,这3个点投票。于是绿色的这个待分类点属于红色的三角形
假设K=5。那么离绿色点近期的有2个红色三角形和3个蓝色的正方形,这5个点投票,于是绿色的这个待分类点属于蓝色的正方形
我们能够看到。KNN本质是基于一种数据统计的方法!
事实上非常多机器学习算法也是基于数据统计的。
KNN是一种memory-based learning,也叫instance-based learning。属于lazy learning。即它没有明显的前期训练过程,而是程序開始执行时,把数据集载入到内存后,不须要进行训练,就能够開始分类了。
详细是每次来一个未知的样本点。就在附近找K个近期的点进行投票。
再举一个样例。Locally weighted regression (LWR)也是一种 memory-based 方法。例如以下图所看到的的数据集。

用不论什么一条直线来模拟这个数据集都是不行的,由于这个数据集看起来不像是一条直线。可是每一个局部范围内的数据点,能够觉得在一条直线上。每次来了一个位置样本x。我们在X轴上以该数据样本为中心,左右各找几个点,把这几个样本点进行线性回归。算出一条局部的直线。然后把位置样本x代入这条直线,就算出了相应的y。完毕了一次线性回归。也就是每次来一个数据点,都要训练一条局部直线,也即训练一次,就用一次。LWR和KNN非常相似,都是为位置数据量身定制,在局部进行训练。
|
KNN |
K-Means |
|
1.KNN是分类算法
2.监督学习 3.喂给它的数据集是带label的数据。已经是全然正确的数据 |
1.K-Means是聚类算法
2.非监督学习 3.喂给它的数据集是无label的数据。是杂乱无章的。经过聚类后才变得有点顺序。先无序。后有序 |
| 没有明显的前期训练过程,属于memory-based learning | 有明显的前期训练过程 |
| K的含义:来了一个样本x,要给它分类,即求出它的y。就从数据集中。在x附近找离它近期的K个数据点,这K个数据点,类别c占的个数最多,就把x的label设为c | K的含义:K是人工固定好的数字,如果数据集合能够分为K个簇,因为是依靠人工定好,须要一点先验知识 |
|
|
|
|
相似点:都包括这种过程,给定一个点,在数据集中找离它近期的点。 即二者都用到了NN(Nears Neighbor)算法,一般用KD树来实现NN。 |
|
标签:jpg img lock euc label 介绍 计算 选择 技术分享
原文地址:http://www.cnblogs.com/jzdwajue/p/7222398.html