标签：公式 脚本 ide dict gif ack 逻辑回归 lam state
一 矩阵求导
复杂矩阵问题求导方法：可以从小到大，从scalar到vector再到matrix。
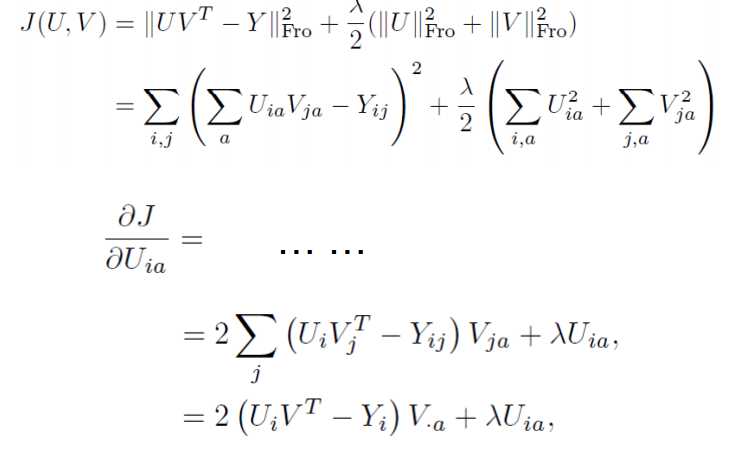
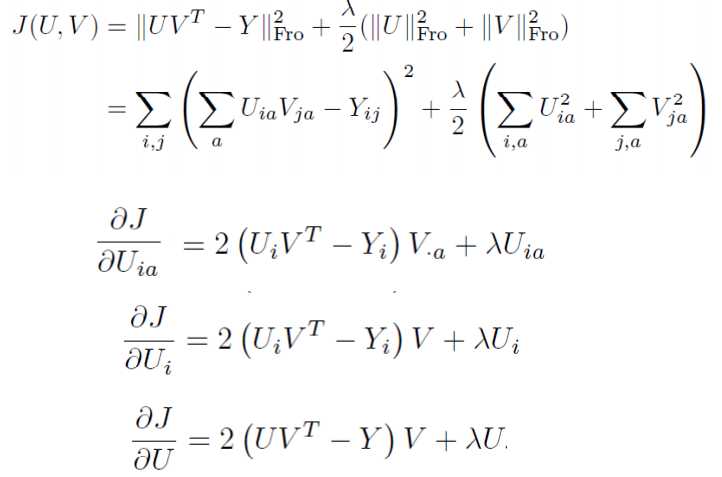
x is a column vector, A is a matrix
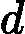
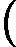
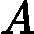
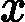
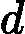
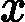
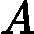d(A?x)/dx=A
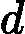
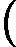
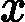
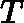
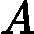
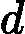
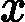
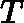
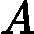d(xT?A)/dxT=A
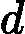
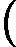
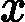
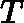
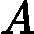
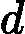
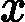
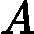
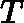d(xT?A)/dx=AT
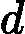
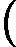
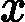
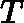
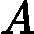
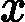
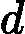
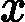
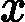
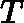
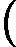
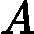
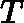
d(xT?A?x)/dx=xT(AT+A)
practice:
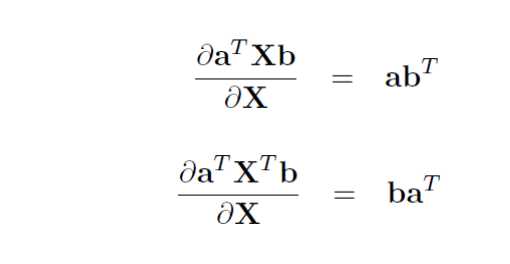
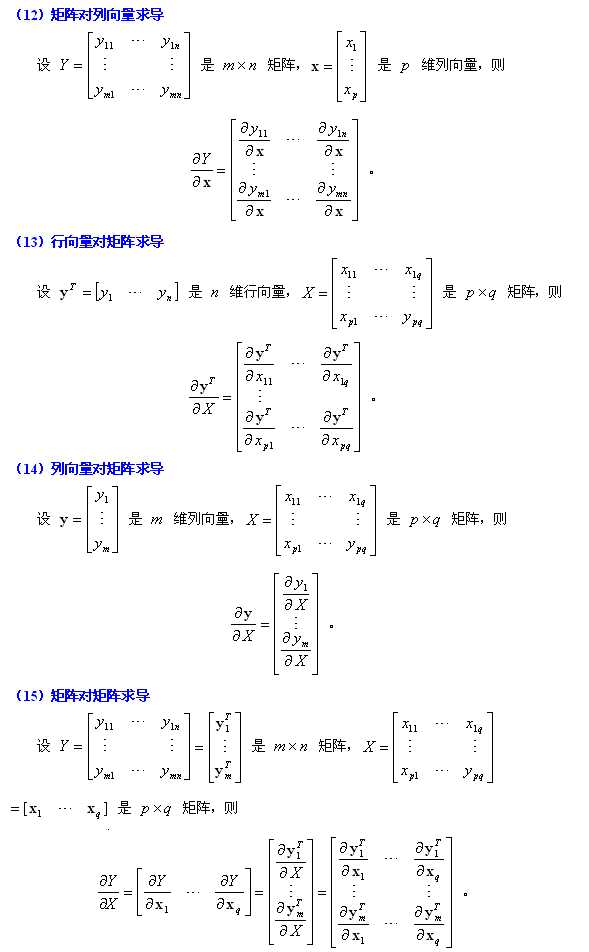
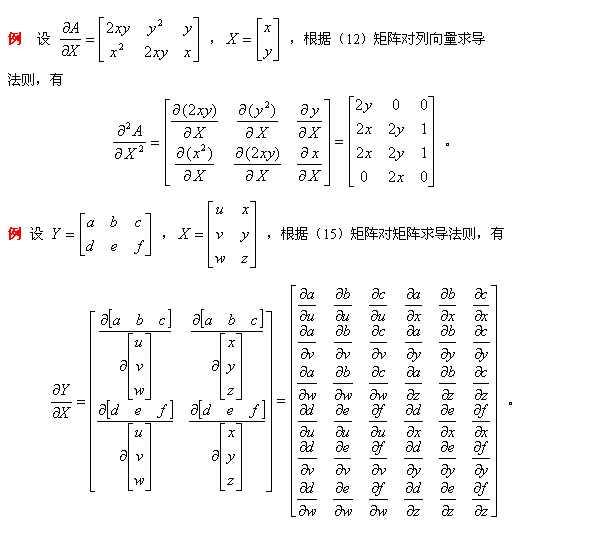
常用的举证求导公式如下：
Y = A * X --> DY/DX = A‘
Y = X * A --> DY/DX = A
Y = A‘ * X * B --> DY/DX = A * B‘
Y = A‘ * X‘ * B --> DY/DX = B * A‘
1. 矩阵Y对标量x求导：
相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了
Y = [y(ij)] --> dY/dx = [dy(ji)/dx]
2. 标量y对列向量X求导：
注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量
y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)‘
3. 行向量Y‘对列向量X求导：
注意1×M向量对N×1向量求导后是N×M矩阵。
将Y的每一列对X求偏导，将各列构成一个矩阵。
重要结论：
dX‘/dX = I
d(AX)‘/dX = A‘
4. 列向量Y对行向量X’求导：
转化为行向量Y’对列向量X的导数，然后转置。
注意M×1向量对1×N向量求导结果为M×N矩阵。
dY/dX‘ = (dY‘/dX)‘
5. 向量积对列向量X求导运算法则：
注意与标量求导有点不同。
d(UV‘)/dX = (dU/dX)V‘ + U(dV‘/dX)
d(U‘V)/dX = (dU‘/dX)V + (dV‘/dX)U
重要结论：
d(X‘A)/dX = (dX‘/dX)A + (dA/dX)X‘ = IA + 0X‘ = A
d(AX)/dX‘ = (d(X‘A‘)/dX)‘ = (A‘)‘ = A
d(X‘AX)/dX = (dX‘/dX)AX + (d(AX)‘/dX)X = AX + A‘X
6. 矩阵Y对列向量X求导：
将Y对X的每一个分量求偏导，构成一个超向量。
注意该向量的每一个元素都是一个矩阵。
7. 矩阵积对列向量求导法则：
d(uV)/dX = (du/dX)V + u(dV/dX)
d(UV)/dX = (dU/dX)V + U(dV/dX)
重要结论：
d(X‘A)/dX = (dX‘/dX)A + X‘(dA/dX) = IA + X‘0 = A
8. 标量y对矩阵X的导数：
类似标量y对列向量X的导数，
把y对每个X的元素求偏导，不用转置。
dy/dX = [ Dy/Dx(ij) ]
重要结论：
y = U‘XV = ΣΣu(i)x(ij)v(j) 于是 dy/dX = [u(i)v(j)] = UV‘
y = U‘X‘XU 则 dy/dX = 2XUU‘
y = (XU-V)‘(XU-V) 则 dy/dX = d(U‘X‘XU - 2V‘XU + V‘V)/dX = 2XUU‘ - 2VU‘ + 0 = 2(XU-V)U‘
9. 矩阵Y对矩阵X的导数：
将Y的每个元素对X求导，然后排在一起形成超级矩阵。
10. 乘积的导数
d(f*g)/dx=(df‘/dx)g+(dg/dx)f‘
结论
d(x‘Ax)=(d(x‘‘)/dx)Ax+(d(Ax)/dx)(x‘‘)=Ax+A‘x （注意：‘‘是表示两次转置）
二 线性模型
2.1 普通的最小二乘
由 LinearRegression 函数实现。最小二乘法的缺点是依赖于自变量的相关性，当出现复共线性时，设计阵会接近奇异，因此由最小二乘方法得到的结果就非常敏感，如果随机误差出现什么波动，最小二乘估计也可能出现较大的变化。而当数据是由非设计的试验获得的时候，复共线性出现的可能性非常大。
1 print __doc__
2
3 import pylab as pl
4 import numpy as np
5 from sklearn import datasets, linear_model
6
7 diabetes = datasets.load_diabetes() #载入数据
8
9 diabetes_x = diabetes.data[:, np.newaxis]
10 diabetes_x_temp = diabetes_x[:, :, 2]
11
12 diabetes_x_train = diabetes_x_temp[:-20] #训练样本
13 diabetes_x_test = diabetes_x_temp[-20:] #检测样本
14 diabetes_y_train = diabetes.target[:-20]
15 diabetes_y_test = diabetes.target[-20:]
16
17 regr = linear_model.LinearRegression()
18
19 regr.fit(diabetes_x_train, diabetes_y_train)
20
21 print ‘Coefficients :\n‘, regr.coef_
22
23 print ("Residual sum of square: %.2f" %np.mean((regr.predict(diabetes_x_test) - diabetes_y_test) ** 2))
24
25 print ("variance score: %.2f" % regr.score(diabetes_x_test, diabetes_y_test))
26
27 pl.scatter(diabetes_x_test,diabetes_y_test, color = ‘black‘)
28 pl.plot(diabetes_x_test, regr.predict(diabetes_x_test),color=‘blue‘,linewidth = 3)
29 pl.xticks(())
30 pl.yticks(())
31 pl.show()
2.2 岭回归
岭回归是一种正则化方法，通过在损失函数中加入L2范数惩罚项，来控制线性模型的复杂程度，从而使得模型更稳健。
from sklearn import linear_model
clf = linear_model.Ridge (alpha = .5)
clf.fit([[0,0],[0,0],[1,1]],[0,.1,1])
clf.coef_
2.3 Lassio
asso和岭估计的区别在于它的惩罚项是基于L1范数的。因此，它可以将系数控制收缩到0，从而达到变量选择的效果。它是一种非常流行的变量选择 方法。Lasso估计的算法主要有两种，其一是用于以下介绍的函数Lasso的coordinate descent。另外一种则是下面会介绍到的最小角回归。
clf = linear_model.Lasso(alpha = 0.1)
clf.fit([[0,0],[1,1]],[0,1])
clf.predict([[1,1]])
2.4 Elastic Net
ElasticNet是对Lasso和岭回归的融合，其惩罚项是L1范数和L2范数的一个权衡。下面的脚本比较了Lasso和Elastic Net的回归路径，并做出了其图形。
1 print __doc__
2
3 # Author: Alexandre Gramfort
4
5
6 # License: BSD Style.
7
8 import numpy as np
9 import pylab as pl
10
11 from sklearn.linear_model import lasso_path, enet_path
12 from sklearn import datasets
13
14 diabetes = datasets.load_diabetes()
15 X = diabetes.data
16 y = diabetes.target
17
18 X /= X.std(0) # Standardize data (easier to set the l1_ratio parameter)
19
20 # Compute paths
21
22 eps = 5e-3 # the smaller it is the longer is the path
23
24 print "Computing regularization path using the lasso..."
25 models = lasso_path(X, y, eps=eps)
26 alphas_lasso = np.array([model.alpha for model in models])
27 coefs_lasso = np.array([model.coef_ for model in models])
28
29 print "Computing regularization path using the positive lasso..."
30 models = lasso_path(X, y, eps=eps, positive=True)#lasso path
31 alphas_positive_lasso = np.array([model.alpha for model in models])
32 coefs_positive_lasso = np.array([model.coef_ for model in models])
33
34 print "Computing regularization path using the elastic net..."
35 models = enet_path(X, y, eps=eps, l1_ratio=0.8)
36 alphas_enet = np.array([model.alpha for model in models])
37 coefs_enet = np.array([model.coef_ for model in models])
38
39 print "Computing regularization path using the positve elastic net..."
40 models = enet_path(X, y, eps=eps, l1_ratio=0.8, positive=True)
41 alphas_positive_enet = np.array([model.alpha for model in models])
42 coefs_positive_enet = np.array([model.coef_ for model in models])
43
44 # Display results
45
46 pl.figure(1)
47 ax = pl.gca()
48 ax.set_color_cycle(2 * [‘b‘, ‘r‘, ‘g‘, ‘c‘, ‘k‘])
49 l1 = pl.plot(coefs_lasso)
50 l2 = pl.plot(coefs_enet, linestyle=‘--‘)
51
52 pl.xlabel(‘-Log(lambda)‘)
53 pl.ylabel(‘weights‘)
54 pl.title(‘Lasso and Elastic-Net Paths‘)
55 pl.legend((l1[-1], l2[-1]), (‘Lasso‘, ‘Elastic-Net‘), loc=‘lower left‘)
56 pl.axis(‘tight‘)
57
58 pl.figure(2)
59 ax = pl.gca()
60 ax.set_color_cycle(2 * [‘b‘, ‘r‘, ‘g‘, ‘c‘, ‘k‘])
61 l1 = pl.plot(coefs_lasso)
62 l2 = pl.plot(coefs_positive_lasso, linestyle=‘--‘)
63
64 pl.xlabel(‘-Log(lambda)‘)
65 pl.ylabel(‘weights‘)
66 pl.title(‘Lasso and positive Lasso‘)
67 pl.legend((l1[-1], l2[-1]), (‘Lasso‘, ‘positive Lasso‘), loc=‘lower left‘)
68 pl.axis(‘tight‘)
69
70 pl.figure(3)
71 ax = pl.gca()
72 ax.set_color_cycle(2 * [‘b‘, ‘r‘, ‘g‘, ‘c‘, ‘k‘])
73 l1 = pl.plot(coefs_enet)
74 l2 = pl.plot(coefs_positive_enet, linestyle=‘--‘)
75
76 pl.xlabel(‘-Log(lambda)‘)
77 pl.ylabel(‘weights‘)
78 pl.title(‘Elastic-Net and positive Elastic-Net‘)
79 pl.legend((l1[-1], l2[-1]), (‘Elastic-Net‘, ‘positive Elastic-Net‘),
80 loc=‘lower left‘)
81 pl.axis(‘tight‘)
82 pl.show()
2.5 逻辑回归
Logistic回归是一个线性分类器。类 LogisticRegression 实现了该分类器，并且实现了L1范数，L2范数惩罚项的logistic回归。为了使用逻辑回归模型，我对鸢尾花进行分类。鸢尾花数据集一共150个数据，这些数据分为3类（分别为setosa，versicolor,virginica），每类50个数据。每个数据包含4个属性：萼片长度，萼片宽度，花瓣长度，花瓣宽度。具体代码如下：
1 import matplotlib.pyplot as plt
2 import numpy as np
3 from sklearn import datasets,linear_model,discriminant_analysis,cross_validation
4
5 def load_data():
6 iris=datasets.load_iris()
7 X_train=iris.data
8 Y_train=iris.target
9 return cross_validation.train_test_split(X_train,Y_train,test_size=0.25,random_state=0,stratify=Y_train)
10
11 def test_LogisticRegression(*data): # default use one vs rest
12 X_train, X_test, Y_train, Y_test = data
13 regr=linear_model.LogisticRegression()
14 regr.fit(X_train,Y_train)
15 print("Coefficients:%s, intercept %s"%(regr.coef_,regr.intercept_))
16 print("Score:%.2f"%regr.score(X_test,Y_test))
17
18 def test_LogisticRegression_multionmial(*data): #use multi_class
19 X_train, X_test, Y_train, Y_test = data
20 regr=linear_model.LogisticRegression(multi_class=‘multinomial‘,solver=‘lbfgs‘)
21 regr.fit(X_train,Y_train)
22 print(‘Coefficients:%s, intercept %s‘%(regr.coef_,regr.intercept_))
23 print("Score:%2f"%regr.score(X_test,Y_test))
24
25 def test_LogisticRegression_C(*data):#C is the reciprocal of the regularization term
26 X_train, X_test, Y_train, Y_test = data
27 Cs=np.logspace(-2,4,num=100) #create equidistant series
28 scores=[]
29 for C in Cs:
30 regr=linear_model.LogisticRegression(C=C)
31 regr.fit(X_train,Y_train)
32 scores.append(regr.score(X_test,Y_test))
33 fig=plt.figure()
34 ax=fig.add_subplot(1,1,1)
35 ax.plot(Cs,scores)
36 ax.set_xlabel(r"C")
37 ax.set_ylabel(r"score")
38 ax.set_xscale(‘log‘)
39 ax.set_title("logisticRegression")
40 plt.show()
41
42 X_train,X_test,Y_train,Y_test=load_data()
43 test_LogisticRegression(X_train,X_test,Y_train,Y_test)
44 test_LogisticRegression_multionmial(X_train,X_test,Y_train,Y_test)
45 test_LogisticRegression_C(X_train,X_test,Y_train,Y_test)
结果输出如下：
可见多分类策略可以提高准确率。
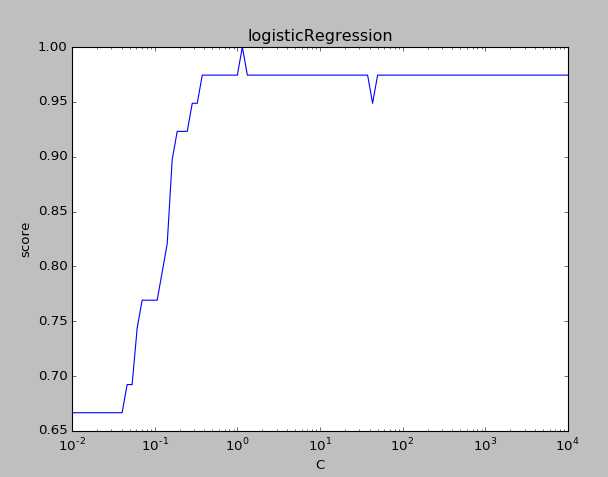
可见随着C的增大，预测的准确率也是在增大的。当C增大到一定的程度，预测的准确率维持在较高的水准保持不变。
2.6 线性判别分析
这里同样适用鸢尾花的数据，具体代码如下：
1 import matplotlib.pyplot as plt 2 import numpy as np 3 from sklearn import datasets,linear_model,discriminant_analysis,cross_validation 4 5 def load_data(): 6 iris=datasets.load_iris() 7 X_train=iris.data 8 Y_train=iris.target 9 return cross_validation.train_test_split(X_train,Y_train,test_size=0.25,random_state=0,stratify=Y_train) 10 11 def test_LinearDiscriminantAnalysis(*data): 12 X_train,X_test,Y_train,Y_test=data 13 lda=discriminant_analysis.LinearDiscriminantAnalysis() 14 lda.fit(X_train,Y_train) 15 print("Coefficients:%s, intercept %s"%(lda.coef_,lda.intercept_)) 16 print("Score:%.2f"%lda.score(X_test,Y_test)) 17 18 19 20 def plot_LDA(converted_X,Y): 21 from mpl_toolkits.mplot3d import Axes3D 22 fig=plt.figure() 23 ax=Axes3D(fig) 24 colors=‘rgb‘ 25 markers=‘o*s‘ 26 for target,color,marker in zip([0,1,2],colors,markers): 27 pos=(Y==target).ravel() 28 X=converted_X[pos,:] 29 ax.scatter(X[:,0],X[:,1],X[:,2],color=color,marker=marker,label="Label %d"%target) 30 ax.legend(loc="best") 31 fig.suptitle("Iris After LDA") 32 plt.show() 33 34 X_train,X_test,Y_train,Y_test=load_data() 35 test_LinearDiscriminantAnalysis(X_train,X_test,Y_train,Y_test) 36 X=np.vstack((X_train,X_test)) 37 Y=np.vstack((Y_train.reshape(Y_train.size,1),Y_test.reshape(Y_test.size,1))) 38 lda=discriminant_analysis.LinearDiscriminantAnalysis() 39 lda.fit(X,Y) 40 converted_X=np.dot(X,np.transpose(lda.coef_))+lda.intercept_ 41 plot_LDA(converted_X,Y)
运行结果如下：
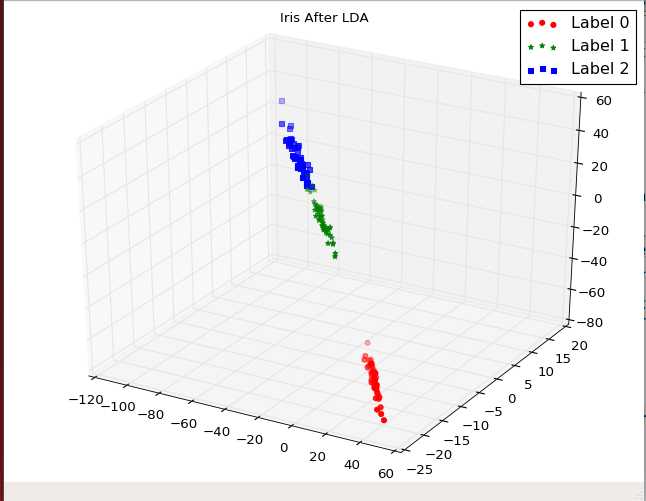
可以看出经过线性判别分析之后，不同种类的鸢尾花之间的间隔较远；相同种类的鸢尾花之间的已经相互聚集了
标签：公式 脚本 ide dict gif ack 逻辑回归 lam state
原文地址：http://www.cnblogs.com/acm-jing/p/7230790.html
