标签:最可 div 介绍 png category 统计 贝叶斯分类器 tin nio
1、朴素贝叶斯算法介绍
一个待分类项x=(a,b,c...),判断x属于y1,y2,y3...类别中的哪一类。
贝叶斯公式:
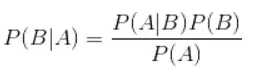
算法定义如下:
(1)、设x={a1, a2, a3, ...}为一个待分类项,而a1, a2, a3...分别为x的特征
(2)、有类别集合C={y1, y2, y3, ..}
(3)、计算p(y1|x), p(y2|x), p(y3|x), ....
(4)、如果p(y(k)|x)=max{p(y1|x), p(y2|x), p(y3|x), ....},则x属于p(y(k)|x)
计算:
(1)、找到一个已知分类的待分类项集合,也就是训练集。
(2)、统计得到在各个类别下各个特征属性的条件概率估计。即:
p(a1|y1).................... p(am|y1)
.
.
.
p(a1|yn).................... p(an|yn)
(3)、如果各个特征属性是条件独立的,则根据贝叶斯公式:

2、病人分类的例子
让我从一个例子开始讲起,你会看到贝叶斯分类器很好懂,一点都不难。
某个医院早上收了六个门诊病人,如下表。
症状 职业 疾病
打喷嚏 护士 感冒
打喷嚏 农夫 过敏
头痛 建筑工人 脑震荡
头痛 建筑工人 感冒
打喷嚏 教师 感冒
头痛 教师 脑震荡
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒)
/ P(打喷嚏x建筑工人)
假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
/ P(打喷嚏) x P(建筑工人)
这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
3、Python实现
from numpy import * def loadDataSet(): postingList=[[‘my‘, ‘dog‘, ‘has‘, ‘flea‘, ‘problems‘, ‘help‘, ‘please‘], [‘maybe‘, ‘not‘, ‘take‘, ‘him‘, ‘to‘, ‘dog‘, ‘park‘, ‘stupid‘], [‘my‘, ‘dalmation‘, ‘is‘, ‘so‘, ‘cute‘, ‘I‘, ‘love‘, ‘him‘], [‘stop‘, ‘posting‘, ‘stupid‘, ‘worthless‘, ‘garbage‘], [‘mr‘, ‘licks‘, ‘ate‘, ‘my‘, ‘steak‘, ‘how‘, ‘to‘, ‘stop‘, ‘him‘], [‘quit‘, ‘buying‘, ‘worthless‘, ‘dog‘, ‘food‘, ‘stupid‘]] classVec = [0,1,0,1,0,1] #1 is abusive, 0 not return postingList,classVec def createVocabList(dataSet): vocabSet = set([]) #create empty set for document in dataSet: vocabSet = vocabSet | set(document) #union of the two sets return list(vocabSet) def setOfWords2Vec(vocabList, inputSet): returnVec = [0]*len(vocabList) for word in inputSet: if word in vocabList: returnVec[vocabList.index(word)] = 1 else: print "the word: %s is not in my Vocabulary!" % word return returnVec def trainNB0(trainMatrix,trainCategory): numTrainDocs = len(trainMatrix) numWords = len(trainMatrix[0]) pAbusive = sum(trainCategory)/float(numTrainDocs) p0Num = ones(numWords); p1Num = ones(numWords) #change to ones() p0Denom = 2.0; p1Denom = 2.0 #change to 2.0 for i in range(numTrainDocs): if trainCategory[i] == 1: p1Num += trainMatrix[i] p1Denom += sum(trainMatrix[i]) else: p0Num += trainMatrix[i] p0Denom += sum(trainMatrix[i]) p1Vect = log(p1Num/p1Denom) #change to log() p0Vect = log(p0Num/p0Denom) #change to log() return p0Vect,p1Vect,pAbusive def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1): p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1) if p1 > p0: return 1 else: return 0 def bagOfWords2VecMN(vocabList, inputSet): returnVec = [0]*len(vocabList) for word in inputSet: if word in vocabList: returnVec[vocabList.index(word)] += 1 return returnVec def testingNB(): listOPosts,listClasses = loadDataSet() myVocabList = createVocabList(listOPosts) trainMat=[] for postinDoc in listOPosts: trainMat.append(setOfWords2Vec(myVocabList, postinDoc)) p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses)) testEntry = [‘love‘, ‘my‘, ‘dalmation‘] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry,‘classified as: ‘,classifyNB(thisDoc,p0V,p1V,pAb) testEntry = [‘stupid‘, ‘garbage‘] thisDoc = array(setOfWords2Vec(myVocabList, testEntry)) print testEntry,‘classified as: ‘,classifyNB(thisDoc,p0V,p1V,pAb)
标签:最可 div 介绍 png category 统计 贝叶斯分类器 tin nio
原文地址:http://www.cnblogs.com/lovephysics/p/7236433.html