标签:优先 init 在线 深度优先 不清楚 搜索 基本 href har
一、梳理概念
定义:对于有根树T的两个结点u、v,最近公共祖先LCA(T,u,v)表示一个结点x,满足x是u、v的祖先且x的深度尽可能大。
通俗地讲,最近公共祖先节点,就是两个节点在这棵树上深度最大的公共的祖先节点,即两个点在这棵树上距离最近的公共祖先节点。
提示:父亲节点也是祖先节点,节点本身也是它的祖先节点。
给出一棵树,如图所示:
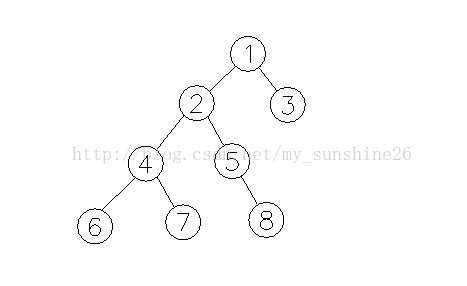
由上面的定义可知:3和5的最近公共祖先为1,5和6的最近公共祖先为2,2和7的最近公共祖先为2, 6和7的最近公共祖先为4。
二、繁文缛节
注意注意注意!!!尚不清楚二叉树的后序遍历、并查集、tarjan算法的童鞋可以不要往下看了。
【解决LCA问题——Tarjan 离线算法】
简介:利用并查集在一次DFS(深度优先遍历)中完成所有询问。换句话说,要所有询问都读入后才开始计算,所以是一种离线的算法。
二叉树后序遍历的性质:当两个节点(u,v)的最近公共祖先是x时,进行后序遍历的时候,必然先访问完x的所有子树(其中包含u、v),然后才会返回到x所在的节点。这个性质就是我们使用Tarjan算法解决最近公共祖先问题的核心思想。
用图讲算法:
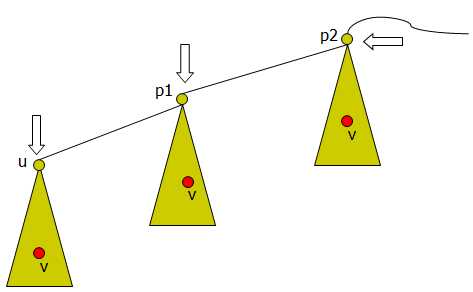
如上图所示,找出根节点root到节点u的关键路径P(解释一下,关键路径P内容为root-->…-->p2-->p1-->u),已遍历的点位于路径P中某个节点(譬如说p2)的子树中(因为上面几行的后序遍历性质说明了后访问子树根节点)。第一种情况:当遍历到u时v已遍历过(u的子树已遍历完,因为u为子树根节点),那么v必然存在于子树pk中(也可以在u的子树中),此时LCA(u,v)就等于现在v所在集合的祖先pk(嘿嘿,你画个图就能看明白,因为u是路径P上最后一个根节点,如果v在u的子树中,那么最近公共祖先就是u);第二种情况:如果v还没有遍历到,则继续遍历,只不过LCA(u,v)要等到遍历到v时才能知道了,原理如上。需要注意的一点是,为了保持上图的性质,如果一个节点的一个子树遍历完了,需要合并该节点的子树集合。
三、算法描述
首先我们看一下都有哪些求公共最近祖先的算法并分析一下这些算法的性能,在这里我们设询问次数为q(询问次数是什么?往下读你会懂的):
【Tarjan算法过程模拟】
首先,上图:

条件:我们需要寻找最近公共祖先的点对为<3,5>,<5,6>,<2,7>,<6,7>。
初始化:①开一个pre数组,记录父亲节点,初始化pre[i]=i;②再开一个vis数组,记录节点是否已经访问,初始化 memset(vis,0,sizeof(vis))。
过程:
至此,完成求最小公共祖先的操作。
四、代码模板
由于LCA的题目千变万化,下面给出最基础的模板(给出一系列边用邻接表保存,把询问也用邻接表保存,只求LCA,不维护其他值)
void Tarjan(int now)
{
vis[now]=1;
for(int i=head1[now];i!=-1;i=e1[i].next)
{
int t=e1[i].t;
if(vis[t]==0)
{
Tarjan(t);
join(now,t);
}
}
for(int i=head2[now];i!=-1;i=e2[i].next)
{
int t=e2[i].t;
if(vis[t]==1)
{
e2[i].lca=find(t);
e2[i^1].lca=e2[i].lca;
}
}
}
五、沙场练兵
题目:POJ 1470
代码:
/*
* POJ 1470
* 给出一颗有向树,Q个查询
* 输出查询结果中每个点出现次数
*/
/*
* LCA离线算法,Tarjan
* 复杂度O(n+Q);
*/
const int MAXN = 1010;
const int MAXQ = 500010;//查询数的最大值
//并查集部分
int F[MAXN];//需要初始化为-1
int find(int x)
{
if(F[x] == -1)return x;
return F[x] = find(F[x]);
}
void bing(int u,int v)
{
int t1 = find(u);
int t2 = find(v);
if(t1 != t2)
F[t1] = t2;
}
//************************
bool vis[MAXN];//访问标记
int ancestor[MAXN];//祖先
struct Edge
{
int to,next;
}edge[MAXN*2];
int head[MAXN],tot;
void addedge(int u,int v)
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
struct Query
{
int q,next;
int index;//查询编号
}query[MAXQ*2];
int answer[MAXQ];//存储最后的查询结果,下标0~Q-1
int h[MAXQ];
int tt;
int Q;
void add_query(int u,int v,int index)
{
query[tt].q = v;
query[tt].next = h[u];
query[tt].index = index;
h[u] = tt++;
query[tt].q = u;
query[tt].next = h[v];
query[tt].index = index;
h[v] = tt++;
}
void init()
{
tot = 0;
memset(head,-1,sizeof(head));
tt = 0;
memset(h,-1,sizeof(h));
memset(vis,false,sizeof(vis));
memset(F,-1,sizeof(F));
memset(ancestor,0,sizeof(ancestor));
}
void LCA(int u)
{
ancestor[u] = u;
vis[u] = true;
for(int i = head[u];i != -1;i = edge[i].next)
{
int v = edge[i].to;
if(vis[v])continue;
LCA(v);
bing(u,v);
ancestor[find(u)] = u;
}
for(int i = h[u];i != -1;i = query[i].next)
{
int v = query[i].q;
if(vis[v])
{
answer[query[i].index] = ancestor[find(v)];
}
}
}
bool flag[MAXN];
int Count_num[MAXN];
int main()
{
int n;
int u,v,k;
while(scanf("%d",&n) == 1)
{
init();
memset(flag,false,sizeof(flag));
for(int i = 1;i <= n;i++)
{
scanf("%d:(%d)",&u,&k);
while(k--)
{
scanf("%d",&v);
flag[v] = true;
addedge(u,v);
addedge(v,u);
}
}
scanf("%d",&Q);
for(int i = 0;i < Q;i++)
{
char ch;
cin>>ch;
scanf("%d %d)",&u,&v);
add_query(u,v,i);
}
int root;
for(int i = 1;i <= n;i++)
if(!flag[i])
{
root = i;
break;
}
LCA(root);
memset(Count_num,0,sizeof(Count_num));
for(int i = 0;i < Q;i++)
Count_num[answer[i]]++;
for(int i = 1;i <= n;i++)
if(Count_num[i] > 0)
printf("%d:%d\n",i,Count_num[i]);
}
return 0;
}
标签:优先 init 在线 深度优先 不清楚 搜索 基本 href har
原文地址:http://www.cnblogs.com/xzxl/p/7237125.html