标签:logs 输入 ++ try equals exception 详细 引用 etl
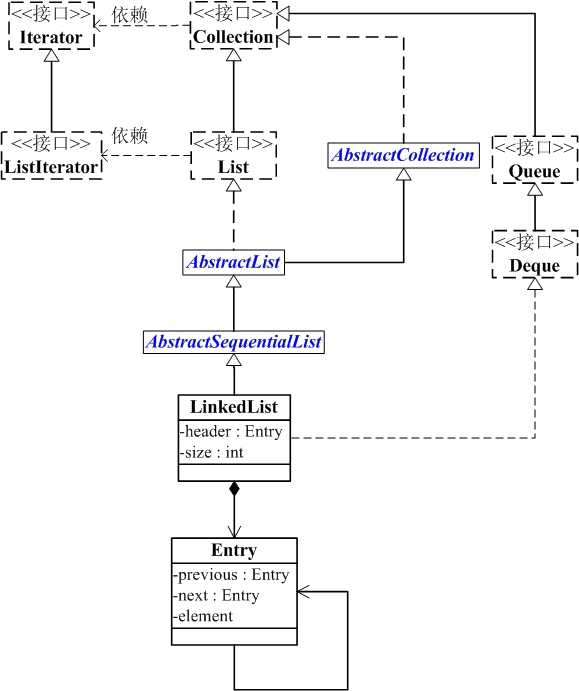
LinkedList的本质是双向链表。
(01) LinkedList继承于AbstractSequentialList,并且实现了Dequeue接口。
(02) LinkedList包含两个重要的成员:header 和 size。
header是双向链表的表头,它是双向链表节点所对应的类Entry的实例。Entry中包含成员变量: previous, next, element。其中,previous是该节点的上一个节点,next是该节点的下一个节点,element是该节点所包含的值。
size是双向链表中节点的个数。
(前面照旧是复制粘贴的图和文字,大家大概理解一下,下面进入正题)
为了理解上面的概念,首先我们来看一下核心类Node
//节点,有前驱,后继和值三个字端,其中前驱和后继也是节点 private static class Node<E> { E item; Node<E> next; Node<E> prev; Node(Node<E> prev, E element, Node<E> next) { this.item = element; this.next = next; this.prev = prev; } }
Node表示的是结点,结点里面有三个元素:
数据,前驱和后继。
其中数据可是任意类型,前驱和后继同样是结点。
我们可以想象一个双向链表依次一共有A,B,C三个结点,他们的数据分别为a,b,c。那么:
A的前驱为null,后继为B,数据为a。
B的前驱为A,后继为C,数据为b。
C的前驱为B,后继为null,数据为c。
接下来我们来看一下构造函数和类变量
//集合元素个数 transient int size = 0; //第一个节点 transient Node<E> first; //最后一个节点 transient Node<E> last; //输入为空的构造函数 public LinkedList() { } //直接传入一个Collection放入LinkedList中的构造器, public LinkedList(Collection<? extends E> c) { //调用无参的构造期 this(); addAll(c); }
类变量分别是List中数据的个数,第一个结点和最后一个结点。
构造函数有两个:一个是空的构造函数,一个是传入一个Collection来生成LinkedList。
我们来具体看一下这个addAll方法
//将指定集合c中所有的元素,按照其迭代器返回的顺序全部追加到集合的结尾。 public boolean addAll(Collection<? extends E> c) { return addAll(size, c); } //将指定集合c中所有的元素,按照其迭代器返回的顺序全部追加到集合的特定位置。 public boolean addAll(int index, Collection<? extends E> c) { checkPositionIndex(index); Object[] a = c.toArray(); int numNew = a.length; if (numNew == 0) return false; //pred是predecessor前置节点,succ是succeed 后置节点,请大家学好英语(笑) Node<E> pred, succ; if (index == size) { //新增节点在最后一个 succ = null; pred = last; } else { //新增结点在index处 succ = node(index); pred = succ.prev; } //前驱节点不为null的情况下,循环生成新节点,把前任节点作为新节点的前驱,数组里的数作为节点的值,后继置为空 //然后把新节点作为前驱的后继,之后把新节点作为前驱,继续循环执行 //可能你这个时候会有疑问,那不是没有制定后继?并不是的,后继是在你的新节点变为前驱后,由 pred.next = newNode;这一句指定的。 for (Object o : a) { @SuppressWarnings("unchecked") E e = (E) o; Node<E> newNode = new Node<>(pred, e, null); if (pred == null) first = newNode; else pred.next = newNode; pred = newNode; } //后继为空,则最后一个就是前驱(也就是前面最后一句指定为前驱的newNode) //后继不为空的话,则把后继作为前驱(就是前面最后一句指定为前驱的newNode)的后继,前驱作为后继的前驱 if (succ == null) { last = pred; } else { pred.next = succ; succ.prev = pred; } //列表里的数增加 size += numNew; //这个用来判断迭代器的fast-fail的,具体见我的前一篇ArrayList的那篇博文 modCount++; return true; }
整个把Collection变为LinkedList的过程写的比较详细了,不再赘述。
现在我们随便看一些常用的方法,比如说获取第一个结点的值,我们发现会有getFirst()和peekFirst()这样两个方法;同样的获取最后一个结点的值,我们发现会有getLast()和peekLast()两个方法。那么为何会有两种呢?
我们看一下源码:
//获取第一个结点的值 public E getFirst() { final Node<E> f = first; if (f == null) throw new NoSuchElementException(); return f.item; } //获取的第一个结点的值 public E peekFirst() { final Node<E> f = first; return (f == null) ? null : f.item; }
我们可以看出来,前者如果结点为空会报错,后者如果结点为空则会返回null。
以下对第一个结点和最后一个结点的操作:
第一个结点(头部) 最后一个结点(尾部)
抛出异常 特殊值 抛出异常 特殊值
插入 addFirst(e) offerFirst(e) addLast(e) offerLast(e)
移除 removeFirst() pollFirst() removeLast() pollLast()
检查 getFirst() peekFirst() getLast() peekLast()
左边的操作遇到异常会抛出异常,右边的操作遇到异常会返回特殊值。
由于LinkedLIst分别实现了队列和栈的接口,以下也是对第一个结点和最后一个结点的操作
当作为队列时,下表的方法等价:
队列方法 等效方法 add(e) addLast(e) offer(e) offerLast(e) remove() removeFirst() poll() pollFirst() element() getFirst() peek() peekFirst()
当作为栈时下表的方法等价:
栈方法 等效方法
push(e) addFirst(e)
pop() removeFirst()
peek() peekFirst()
以上说的都是对第一个结点和最后一个结点的操作,接下来写一下对中间结点的操作:
//返回特定位置的结点的值 public E get(int index) { checkElementIndex(index); return node(index).item; } //替换特定位置的结点的值,返回旧的值 public E set(int index, E element) { checkElementIndex(index); Node<E> x = node(index); E oldVal = x.item; x.item = element; return oldVal; } //替换特定位置的结点,原结点向后移 public void add(int index, E element) { checkPositionIndex(index); if (index == size) linkLast(element); else linkBefore(element, node(index)); } //删除特定位置的结点 public E remove(int index) { checkElementIndex(index); return unlink(node(index)); }
里面的具体操作如下:
//获取某个index的结点 Node<E> node(int index) { // assert isElementIndex(index); if (index < (size >> 1)) { Node<E> x = first; for (int i = 0; i < index; i++) x = x.next; return x; } else { Node<E> x = last; for (int i = size - 1; i > index; i--) x = x.prev; return x; } } //把输入的数e作为新增在最前面的结点的值 private void linkFirst(E e) { final Node<E> f = first; final Node<E> newNode = new Node<>(null, e, f); first = newNode; if (f == null) last = newNode; else f.prev = newNode; size++; modCount++; } //把输入的数e作为新增在最后面的结点的值 void linkLast(E e) { final Node<E> l = last; final Node<E> newNode = new Node<>(l, e, null); last = newNode; if (l == null) first = newNode; else l.next = newNode; size++; modCount++; } //把输入的数e作为新增在结点succ的前面的结点的值 void linkBefore(E e, Node<E> succ) { // assert succ != null; final Node<E> pred = succ.prev; final Node<E> newNode = new Node<>(pred, e, succ); succ.prev = newNode; if (pred == null) first = newNode; else pred.next = newNode; size++; modCount++; } //把非空的LinkedList的第一个节点unlinked(删除) private E unlinkFirst(Node<E> f) { // assert f == first && f != null; final E element = f.item; final Node<E> next = f.next; f.item = null; f.next = null; // help GC first = next; if (next == null) last = null; else next.prev = null; size--; modCount++; return element; } //把非空的LinkedList的最后一个节点unlinked(删除) private E unlinkLast(Node<E> l) { // assert l == last && l != null; final E element = l.item; final Node<E> prev = l.prev; l.item = null; l.prev = null; // help GC last = prev; if (prev == null) first = null; else prev.next = null; size--; modCount++; return element; } ///把非空的LinkedList的某个节点unlinked(删除) E unlink(Node<E> x) { // assert x != null; final E element = x.item; final Node<E> next = x.next; final Node<E> prev = x.prev; if (prev == null) { first = next; } else { prev.next = next; x.prev = null; } if (next == null) { last = prev; } else { next.prev = prev; x.next = null; } x.item = null; size--; modCount++; return element; }
可以从上面看出来新增和删除元素都是比较方便的。
还有两个比较特殊的删除方法:
//删除第一个出现的特定值 public boolean removeFirstOccurrence(Object o) { return remove(o); } //删除最后一个出现的特定值 public boolean removeLastOccurrence(Object o) { if (o == null) { for (Node<E> x = last; x != null; x = x.prev) { if (x.item == null) { unlink(x); return true; } } } else { for (Node<E> x = last; x != null; x = x.prev) { if (o.equals(x.item)) { unlink(x); return true; } } } return false; }
它们的特殊之处在于,它们想要删除的结点的数值也许有很多个,但是它们只会删除第一个出现的或者是最后一个出现的。
然后我们看一下搜索元素的方法:
//判断是否包含某个特定的结点的值 public boolean contains(Object o) { return indexOf(o) != -1; } //查找LinkedList中是否包含某个值,并返回第一个出现这个值的索引值,否则返回-1 public int indexOf(Object o) { int index = 0; if (o == null) { for (Node<E> x = first; x != null; x = x.next) { if (x.item == null) return index; index++; } } else { for (Node<E> x = first; x != null; x = x.next) { if (o.equals(x.item)) return index; index++; } } return -1; } //反向查找LinkedList中是否包含某个值,并返回第一个出现这个值的索引值,否则返回-1 public int lastIndexOf(Object o) { int index = size; if (o == null) { for (Node<E> x = last; x != null; x = x.prev) { index--; if (x.item == null) return index; } } else { for (Node<E> x = last; x != null; x = x.prev) { index--; if (o.equals(x.item)) return index; } } return -1; }
可以看出来,搜索元素是比较麻烦的,必须要全部遍历一遍。
最后我们看一下一些边界值判断的方法:
//判断某个索引值是否存在 private boolean isElementIndex(int index) { return index >= 0 && index < size; } //判断这个索引是否超出了位置的边界,这个和上面的有何区别?为何index是<=而不是< private boolean isPositionIndex(int index) { return index >= 0 && index <= size; } //多种边界异常的判断 private String outOfBoundsMsg(int index) { return "Index: "+index+", Size: "+size; } private void checkElementIndex(int index) { if (!isElementIndex(index)) throw new IndexOutOfBoundsException(outOfBoundsMsg(index)); } private void checkPositionIndex(int index) { if (!isPositionIndex(index)) throw new IndexOutOfBoundsException(outOfBoundsMsg(index)); }
限于篇幅(Lan),其他方法就不一一介绍了。
总结:
1.LinkedList的本质基于双向链表实。
2.LinkedList在查找元素时,必须遍历链表;在新增和删除元素时,只要调整前后的引用就可以了。
3.LinkedList不是线程安全的,同样拥有fast-fail机制。
标签:logs 输入 ++ try equals exception 详细 引用 etl
原文地址:http://www.cnblogs.com/jing-daye/p/7242576.html