标签:图片 union 路径压缩 pac blog 分享 示意图 节点 system
package practice; /*在一个全是点的图中,循环选择两点连通,之后判断两点是否在同一通路*/ public class Testmain { public static void main(String[] args) { UF uf = new UF(10); uf.union(4, 3); uf.union(3, 8); uf.union(6, 5); uf.union(9, 4); uf.union(2, 1); uf.union(5, 0); uf.union(7, 2); uf.union(6, 1); System.out.println(uf.connected(8, 9)); System.out.println(uf.connected(1, 0)); System.out.println(uf.connected(6, 7)); for (int i = 0; i < 10; i++) { System.out.println(uf.find(i)); } } } class UF{ int [] id; //点的父节点 int [] sz; //点的权 /** * @param N 点的个数 */ public UF(int N) { id = new int[N]; sz = new int[N]; for (int i = 0; i < N; i++) { id[i] = i; sz[i] = 1;} } /** * @param p * @param q 要连通的两点 */ void union(int p,int q) { int pboot = find(p); //找到此点的根节点 int qboot = find(q); //同上 if (pboot == qboot) return; //如果在同一通路,返回 if (sz[pboot] >= sz[qboot]) { id[qboot] = pboot; sz[pboot] += sz[qboot];} else { id[qboot] = pboot; sz[qboot] += sz[pboot];} //将权值小的根节点连在权值大的根节点上,并将权值相加赋给连接后的根节点 } /** * @param p 要找的点 * @return p的根节点 */ int find(int p) { int temp = p; while (p != id[p]) { p = id[p];} //一直向上找父节点,直到节点的父节点为自身,则为根节点 while (temp != id[temp]) //将找过的点全部连在根节点上 { int temp2 = temp; temp = id[temp]; id[temp2] = p; } return p; } boolean connected(int p,int q) //判断两点是否连通 { return find(p) == find(q);} }
算法示意图(图片来自《算法(第四版官网)》)
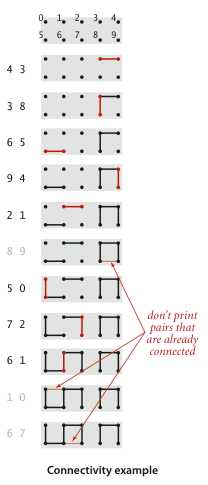
关于加权
给每个节点都赋一个权值,权值可以表示点在树的哪一层,根节点的权值最大,每向下一层权值递减一,最下层权值为一。所一可以通过比较根节点的权值,让层数少的树连在层数大的树上,使最后树的层数更少。
关于路径压缩
在找点的根节点时,直接将点连在根节点上,使树的层数更少,算法更快。
标签:图片 union 路径压缩 pac blog 分享 示意图 节点 system
原文地址:http://www.cnblogs.com/zhangqi66/p/7244650.html