标签:idt 描述 nbsp out i++ oid style 依次 存在
一、前提引入
我们学过了Bellman-Ford算法,现在又要提出这个SPFA算法,为什么呢?
考虑一个随机图(点和边随机生成),除了已确定最短路的顶点与尚未确定最短路的顶点之间的边,其它的边所做的都是无用的,大致描述为下图(分割线以左为已确定最短路的顶点):
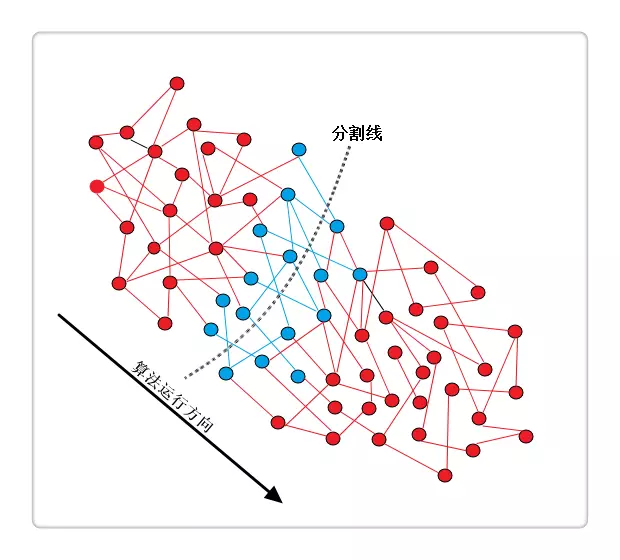
其中红色部分为所做无用的边,蓝色部分为实际有用的边。既然只需用到中间蓝色部分的边,那就是SPFA算法的优势之处了。
二、算法描述
算法特点:在 Bellman-ford 算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。
关键词:初始化 松弛操作 队列
主要变量如下:
int n 表示有n个点,从1~n标号
int s,t s为源点,t为终点
int dis[N] dis[i]表示源点s到点i的最短路径
int pre[N] 记录路径,pre[i]表示i的前驱结点
bool vis[N] vis[i]=true表示点i在队列中
queue<int> q 队列,在整个算法中有顶点入队了要记得标记vis数组,有顶点出队了记得消除那个标记
【初始化】
dis数组全部赋值为INF,pre数组全部赋值为-1(表示还不知道前驱),
dis[s] = 0 表示源点不要求最短路径(或者最短路径就是0)。
【队列+松弛操作】
读取队头顶点u,并将队头顶点u出队(记得消除标记);将与点u相连的所有点v进行松弛操作,如果能更新估计值(即令d[v]变小),那么就更新,另外,如果点v没有在队列中,那么要将点v入队(记得标记),如果已经在队列中了,那么就不用入队,这样不断从队列中取出顶点来进行松弛操作。
以此循环,直到队空为止就完成了单源最短路的求解。
【算法过程】
设立一个队列用来保存待优化的顶点,优化时每次取出队首顶点 u,并且用 u 点当前的最短路径估计值dis[u]对与 u 点邻接的顶点 v 进行松弛操作,如果 v 点的最短路径估计值dis[v]可以更小,且 v 点不在当前的队列中,就将 v 点放入队尾。这样不断从队列中取出顶点来进行松弛操作,直至队列空为止。
【检测负权回路】
方法:如果某个点进入队列的次数大于等于 n,则存在负权回路,其中 n 为图的顶点数。
说明:SPFA无法处理带负环的图。
三、代码实现
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
int matrix[100][100]; //邻接矩阵
bool visited[100]; //标记数组
int dist[100]; //源点到顶点i的最短距离
int path[100]; //记录最短路的路径
int enqueue_num[100]; //记录入队次数
int vertex_num; //顶点数
int edge_num; //边数
int source; //源点
bool SPFA()
{
memset(visited, 0, sizeof(visited));
memset(enqueue_num, 0, sizeof(enqueue_num));
for (int i = 0; i < vertex_num; i++)
{
dist[i] = INT_MAX;
path[i] = source;
}
queue<int> Q;
Q.push(source);
dist[source] = 0;
visited[source] = 1;
enqueue_num[source]++;
while (!Q.empty())
{
int u = Q.front();
Q.pop();
visited[u] = 0;
for (int v = 0; v < vertex_num; v++)
{
if (matrix[u][v] != INT_MAX) //u与v直接邻接
{
if (dist[u] + matrix[u][v] < dist[v])
{
dist[v] = dist[u] + matrix[u][v];
path[v] = u;
if (!visited[v])
{
Q.push(v);
enqueue_num[v]++;
if (enqueue_num[v] >= vertex_num)
return false;
visited[v] = 1;
}
}
}
}
}
return true;
}
void Print()
{
for (int i = 0; i < vertex_num; i++)
{
if (i != source)
{
int p = i;
stack<int> s;
cout << "顶点 " << source << " 到顶点 " << p << " 的最短路径是: ";
while (source != p) //路径顺序是逆向的,所以先保存到栈
{
s.push(p);
p = path[p];
}
cout << source;
while (!s.empty()) //依次从栈中取出的才是正序路径
{
cout << "--" << s.top();
s.pop();
}
cout << " 最短路径长度是:" << dist[i] << endl;
}
}
}
int main()
{
cout << "请输入图的顶点数,边数,源点:";
cin >> vertex_num >> edge_num >> source;
for (int i = 0; i < vertex_num; i++)
for (int j = 0; j < vertex_num; j++)
matrix[i][j] = INT_MAX; //初始化matrix数组
cout << "请输入" << edge_num << "条边的信息:\n";
int u, v, w;
for (int i = 0; i < edge_num; i++)
{
cin >> u >> v >> w;
matrix[u][v] = w;
}
if (SPFA())
Print();
else
cout << "Sorry,it have negative circle!\n";
return 0;
}
标签:idt 描述 nbsp out i++ oid style 依次 存在
原文地址:http://www.cnblogs.com/xzxl/p/7246918.html