标签:tar 最大值 -- alt 另一个 blank lca eof space
LCA的Tarjan算法的时间复杂度为O(n+q)是一种离线算法,要用到并查集。
Tarjan算法基于dfs,在dfs的过程中,对于每个节点位置的询问做出相应的回答。
dfs的过程中,当一棵子树被搜索完成之后,就把他和他的父亲合并成同一集合;在搜索当前子树节点的询问时,如果该询问的另一个节点已经被访问过,那么该编号的询问是被标记了的,于是直接输出当前状态下,另一个节点所在的并查集的祖先;如果另一个节点还没有被访问过,那么就做下标记,继续dfs。
当然,暂时还没那么容易弄懂,所以建议结合下面的例子和标算来看看。
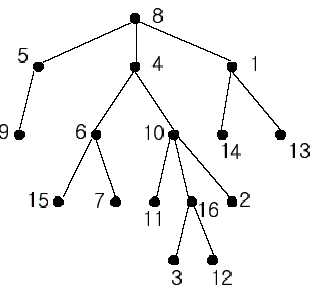
比如:8-1-(13,14),此时如果询问(13,14)的话,则(13,14)的LCA为1;如果没有相应的询问,则往上回溯,(13,14)的父亲都是1了,再往上就是8了。再DFS 8-4-6-(15,7),一样的,回溯时,15,7,4的LCA就成4了。
#include <cstring> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cmath> using namespace std; const int N=40000+5; struct Edge{ int cnt,x[N],y[N],z[N],nxt[N],fst[N]; void set(){ cnt=0; memset(x,0,sizeof x); memset(y,0,sizeof y); memset(z,0,sizeof z); memset(nxt,0,sizeof nxt); memset(fst,0,sizeof fst); } void add(int a,int b,int c){ x[++cnt]=a; y[cnt]=b; z[cnt]=c; nxt[cnt]=fst[a]; fst[a]=cnt; } }e,q; int T,n,m,from,to,dist,in[N],rt,dis[N],fa[N],ans[N]; bool vis[N]; void dfs(int rt){ for (int i=e.fst[rt];i;i=e.nxt[i]){ dis[e.y[i]]=dis[rt]+e.z[i]; dfs(e.y[i]); } } int getf(int k){ return fa[k]==k?k:fa[k]=getf(fa[k]); } void LCA(int rt){ for (int i=e.fst[rt];i;i=e.nxt[i]){ LCA(e.y[i]); fa[getf(e.y[i])]=rt; } vis[rt]=1; for (int i=q.fst[rt];i;i=q.nxt[i]) if (vis[q.y[i]]&&!ans[q.z[i]]) ans[q.z[i]]=dis[q.y[i]]+dis[rt]-2*dis[getf(q.y[i])]; } int main(){ scanf("%d",&T); while (T--){ q.set(),e.set(); memset(in,0,sizeof in); memset(vis,0,sizeof vis); memset(ans,0,sizeof ans); scanf("%d%d",&n,&m); for (int i=1;i<n;i++) scanf("%d%d%d",&from,&to,&dist),e.add(from,to,dist),in[to]++; for (int i=1;i<=m;i++) scanf("%d%d",&from,&to),q.add(from,to,i),q.add(to,from,i); rt=0; for (int i=1;i<=n&&rt==0;i++) if (in[i]==0) rt=i; dis[rt]=0; dfs(rt); for (int i=1;i<=n;i++) fa[i]=i; LCA(rt); for (int i=1;i<=m;i++) printf("%d\n",ans[i]); } return 0; }
LCA_倍增是LCA的在线算法,时间和空间复杂度分别是O((n+q)log n)和O(n log n)。
对于这个算法,我们从最暴力的算法开始:
①如果a和b深度不同,先把深度调浅,使他变得和浅的那个一样
②现在已经保证了a和b的深度一样,所以我们只要把两个一起一步一步往上移动,直到他们到达同一个节点,也就是他们的最近公共祖先了。
#include <cstring> #include <cstdio> #include <cstdlib> #include <algorithm> #include <cmath> #include <vector> using namespace std; const int N=10000+5; vector <int> son[N]; int T,n,depth[N],fa[N],in[N],a,b; void dfs(int prev,int rt){ depth[rt]=depth[prev]+1; fa[rt]=prev; for (int i=0;i<son[rt].size();i++) dfs(rt,son[rt][i]); } int LCA(int a,int b){ if (depth[a]>depth[b]) swap(a,b); while (depth[b]>depth[a]) b=fa[b]; while (a!=b) a=fa[a],b=fa[b]; return a; } int main(){ scanf("%d",&T); while (T--){ scanf("%d",&n); for (int i=1;i<=n;i++) son[i].clear(); memset(in,0,sizeof in); for (int i=1;i<n;i++){ scanf("%d%d",&a,&b); son[a].push_back(b); in[b]++; } depth[0]=-1; int rt=0; for (int i=1;i<=n&&rt==0;i++) if (in[i]==0) rt=i; dfs(0,rt); scanf("%d%d",&a,&b); printf("%d\n",LCA(a,b)); } return 0; }
而实际上,一步一步往上移动太慢,我们可以做一个预处理:
fa[i][j]表示节点i往上走2^j次所到达的祖先,那么不难写出转移方程:
fa[i][0]=father[i],fa[i][j]=fa[fa[i][j-1]][j-1]
然后在求LCA的时候,有这样一个性质:(假设a和b深度一样)
设anst[x][y]为节点x网上走y步到达的祖先,对于一个k,如果anst[a][k]==anst[b][k],那么对于k‘(k‘>k),一定有anst[a][k‘]==anst[b][k‘];对于一个k,如果anst[a][k]!=anst[b][k],那么对于k‘(k‘<k),一定有anst[a][k‘]!=anst[b][k‘],而且LCA(a,b)=LCA(anst[a][k],anst[b][k])。
于是求法就渐渐的现行了:
1. 把a和b移到同一深度(设depth[x]为节点x的深度),假设depth[a]<=depth[b],所以我们的目的是把b向上移动i=(depth[b]-depth[a])层,那么,由于之前有预处理的fa数组,我们把i写成二进制形势,然后利用fa数组来在log n的复杂度中完成;
2. 寻找a和b的LCA下一层的两个祖先。利用之前的那个性质,再利用倍增,如果a和b的第2^k个祖先不是同一个,那么把a改为fa[a][k],b改为fa[b][k],k减1;否则直接k减1;当然在这之前要实现确定k的最大值,从大往小处理下去。最终的结果就是fa[a][0]或者fa[b][0]。
注意点:如果a和b在调节深度之后已经是同一个祖先的,那么直接返回a或者b。
1 #include <cstring> 2 #include <cstdio> 3 #include <cstdlib> 4 #include <algorithm> 5 #include <cmath> 6 #include <vector> 7 using namespace std; 8 const int N=10000+5; 9 vector <int> son[N]; 10 int T,n,depth[N],fa[N][17],in[N],a,b; 11 void dfs(int prev,int rt){ 12 depth[rt]=depth[prev]+1; 13 fa[rt][0]=prev; 14 for (int i=1;(1<<i)<=depth[rt];i++) 15 fa[rt][i]=fa[fa[rt][i-1]][i-1]; 16 for (int i=0;i<son[rt].size();i++) 17 dfs(rt,son[rt][i]); 18 } 19 int LCA(int a,int b){ 20 if (depth[a]>depth[b]) 21 swap(a,b); 22 for (int i=depth[b]-depth[a],j=0;i>0;i>>=1,j++) 23 if (i&1) 24 b=fa[b][j]; 25 if (a==b) 26 return a; 27 int k; 28 for (k=0;(1<<k)<=depth[a];k++); 29 for (;k>=0;k--) 30 if ((1<<k)<=depth[a]&&fa[a][k]!=fa[b][k]) 31 a=fa[a][k],b=fa[b][k]; 32 return fa[a][0]; 33 } 34 int main(){ 35 scanf("%d",&T); 36 while (T--){ 37 scanf("%d",&n); 38 for (int i=1;i<=n;i++) 39 son[i].clear(); 40 memset(in,0,sizeof in); 41 for (int i=1;i<n;i++){ 42 scanf("%d%d",&a,&b); 43 son[a].push_back(b); 44 in[b]++; 45 } 46 depth[0]=-1; 47 int rt=0; 48 for (int i=1;i<=n&&rt==0;i++) 49 if (in[i]==0) 50 rt=i; 51 dfs(0,rt); 52 scanf("%d%d",&a,&b); 53 printf("%d\n",LCA(a,b)); 54 } 55 return 0; 56 }
标签:tar 最大值 -- alt 另一个 blank lca eof space
原文地址:http://www.cnblogs.com/zhouzhendong/p/7256007.html