标签:不用 个数 复杂 括号 左右子树 左右 先来 str return
前言:算法是我们程序员必须修炼的一门内功,作为基本的排序算法,比如快速排序、冒泡排序、堆排序等等都是程序员应该掌握的内容,本节小Y的博客就来聚焦堆排序,来看一下堆排序的源码,一步步分析其过程。
目录:
一:堆排序介绍
二:堆排序源码分析
三:堆排序实例过程
四:总结
一:堆排序介绍
1.1 堆排序
利用堆这种数据结构把数组转化为堆,然后把其转化为最大堆或者最小堆,再对其进行筛选,每次取其顶点,放入数组的最后一个或者第一个,这样数组就是已经排序好的了。每一个数组都可以按照顺序转化为堆:
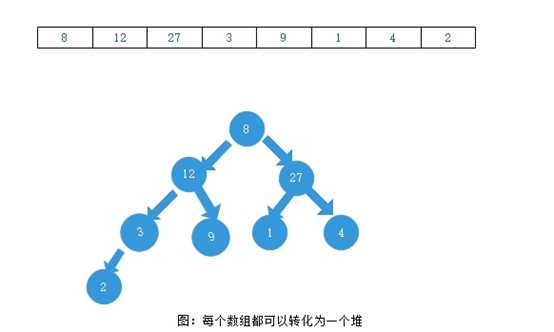
1.2 : 堆的特点
1.2.1:任意一个节点,其父节点的位置是:(当前节点-1)/2,比如上图中的数组(这里说的位置从0开始的,也就是节点值为8的是第一个),比如4这个节点,位置是,那么它的父节点就是(5-1)/2=2,也就是27
1.2.2:每个父节点的左节点的位置是父节点的位置*2,右子节点是父节点*2+1,举个例子。上面的图中的3,作为一个父节点,它的左子树位置是:3*2=6,右子树的位置是3*2+1=7
1.2.3:堆排序中没有左右子树的才进行构建堆,一个堆中没有左右子树的节点的
1.3:堆排序的时间复杂度
堆排序的时间复杂度是0(N),这主要体现在建堆的过程中,首先是左子树进行建堆,其是T(n/2),再对右子树进行建堆,是T(n/2),再对根进行下朔,递推式是T(n)=2*T(n/2)+)(lgn),所以最后的结果是T(n)=O(n);
二:堆排序源码分析
我们先来拟定几个方法来获取节点的位置:
2.1:获取任意节点的父节点,根据当前节点:
private static int getParentIndex(int current) { return (current - 1)/2; }
2.2:根据当前节点获取其左子节点:
private static int getLeftIndex(int current){ return current*2+1; }
2.3:根据当前节点获取其右子节点:
private static int getRightIndex(int current){ return current*2+2; }
这三个方法都是根据堆的特点写的,很简答,1.2已经讲过,不再赘述,
2.4:构建最大堆的方法
private static void maxHeapify(int[] data,int heapSize,int index){ int left=getChildLeftIndex(index);//获取左子节点 int right=getChildRightIndex(index);//获取右子节点 int largeMoreindex=index;//设当前节点是较大的值 if(left<heapSize&&data[index]<data[left]){//比较当前节点的值和左子节点 largeMoreindex=left; } if(right<heapSize&&data[largeMoreindex]<data[right]){ largeMoreindex=right; } if(largeMoreindex!=index){//如果当前节点不是最大值 int temp=data[index]; data[index]=data[largeMoreindex]; data[largeMoreindex]=temp; } If(index!=largeMoreIndex){ maxHeapify (data,heapSize,largeMoreindex); } }
由上面的方法可以看出,是以当前节点的位置,然后获取其左子树的位置,再获取右子树的位置,然后以当前节点和左右子树进行比较,把较大的值的位置存储起来,再进行交换,这样就保证了当前节点的父亲节点是最大值。如果当前节点不是最大值,就进行再次构建堆
此方法需要注意两点:
1:当前节点获取到最大值以后,不能保证交换后的节点的是其子节点中的最大值,所以需要对其进行判断,如果最大值不是当前节点,需要再次递归调用本方法,把交换后的较大的值的传入该方法再次创建最大堆
2:此方法会被多次复用
2.5:对数组进行排序
既然我们已经建好了最大堆,这样就可以把堆的首位进行交换,这样堆的最后一个元素就是最大值,然后放入到数组中最后一个位置,这样就保证了数组的最后一个元素是最大值,循环去调用这个方法,数组就排好序了。这个想法很赞,在这里致敬堆排序的作者。正是他的智慧,我们来享受到如此好的排序算法。
private static void heapSort(int[] array){ for(int i= array.length-1;i>0;i--){ int temp= array [0]; array [0]= array [i]; array [i]=temp; buildmaxHeap(array,i,0); } }
2.6:开始构建堆
我们要写个工具方法已经好了,接下来就是构建堆的过程了,构建堆的过程就是选择堆的最后一个父节点,然后获取其父节点,从末尾向前进行创建堆!
private static void buildMaxHeapify(int[] data){ //创建最大堆 //没有子节点的才需要创建最大堆,从最后一个的父节点开始 int startIndex=getParentIndex(data.length-1); //从尾端开始创建最大堆,每次都是排好的堆 for(int i=startIndex;i>=0;i--){ maxHeapify(data,data.length,i);//创建最大堆的方法 } }
三:堆实例调用的过程
3.1:堆排序写好了,我们来代入一串数组来看一下其过程
设数组为:int[] array={ 1,8,12,6,9,5,7,4} ,将其转化为数组,再选最后一个元素,取其父节点为6,在堆中的位置是3,然后从它开始构堆:
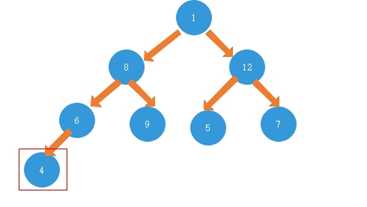
3.2:从6开始进行构建堆,6的左子节点是4,比它小,不用交换顺序。右子节点没有,不用管,即当前节点就是最大值,所以不用再次交换位置
3.3:接下来轮到12,从它开始,位置是2,代入getLeftIndex()方法对应的左子节点是5,也就是节点值为5的那个元素,其右子节点位置是6,也就是对应节点值为7的元素
然后进行比较,其最大的值还是12,所以不用改变
3.4:然后是遍历到8这个节点,发现8的位置其左子节点是6,右子节点是9,进行比较,得出最大的值是9,把9和8的位置进行交换。再对9对应的位置再次建堆,发现其没有左右子节点,所以不用管。
3.4:然后是到顶点,其左子树是9,右子树是12,对应的位置是1,2.先和左边比,较大的largerIndex是1,再把1和2的值进行比较,发现12比9也大,于是largerIndex=2,
然后再把顶点的值和位置是2的节点的值进行交换位置。接下来对其再调用maxHeapify方法,把1和7的元素的位置进行交换,这样数组就变成了这样:
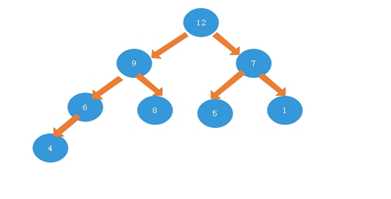
3.5:接下来就是数组排序的过程(重点)
首先进行首位进行交换,就变成了如下图的显示的堆,其12是最大的,放在数组的末尾,其不会再动。那么数组的最后的一个位置的元素就是12
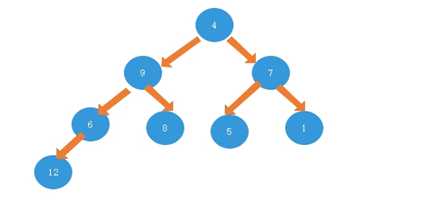
3.6:接下来就是对剩余元素重复这个过程了,直到数组完全排好序。最终的结果是:

四:总结
本篇博客讲解了堆排序的过程,分析了其是如何创建堆的过程,重点在于理解把数组转化为堆这种思想,然后理解堆的特点,把数组当做堆去处理,进行节点的交换,选取最大值,最终再首尾交换,最终得出排序好的数组。
附带堆排序完整代码:

1 package com.wyq.HeapSort; 2 3 public class HeapSort{ 4 private static int[] array=new int[]{9,3,5,2,7,1,3,12}; 5 6 public static void main(String[] args){ 7 buildMaxHeapify(array); 8 heapSort(array); 9 print(array); 10 } 11 12 private static void buildMaxHeapify(int[] data){ //创建最大堆 13 //没有子节点的才需要创建最大堆,从最后一个的父节点开始 14 int startIndex=getParentIndex(data.length-1); 15 //从尾端开始创建最大堆,每次都是排好的堆 16 for(int i=startIndex;i>=0;i--){ 17 maxHeapify(data,data.length,i);//创建最大堆的方法 18 } 19 } 20 21 /** 22 *创建最大堆 23 * 24 *@paramdata 25 *@paramheapSize需要创建最大堆的大小,一般在sort的时候用到,因为最多值放在末尾,末尾就不再归入最大堆了 26 *@paramindex当前需要创建最大堆的位置 27 */ 28 private static void maxHeapify(int[] data,int heapSize,int index){ 29 //当前点与左右子节点比较 30 int left=getChildLeftIndex(index);//获取左子节点 31 int right=getChildRightIndex(index);//获取右子节点 32 33 int largeMoreindex=index; 34 if(left<heapSize&&data[index]<data[left]){ 35 largeMoreindex=left; 36 } 37 if(right<heapSize&&data[largeMoreindex]<data[right]){ 38 largeMoreindex=right; 39 } 40 //得到最大值后可能需要交换,如果交换了,其子节点可能就不是最大堆了,需要重新调整 41 if(largeMoreindex!=index){//交换位置 42 int temp=data[index]; 43 data[index]=data[largeMoreindex];// 44 data[largeMoreindex]=temp; 45 maxHeapify(data,heapSize,largeMoreindex); 46 } 47 } 48 49 /** 50 *排序,最大值放在末尾,data虽然是最大堆,在排序后就成了递增的 51 * 52 *@paramdata 53 */ 54 private static void heapSort(int[] data){ 55 //末尾与头交换,交换后调整最大堆 56 for(int i=data.length-1;i>0;i--){ 57 int temp=data[0]; 58 data[0]=data[i]; 59 data[i]=temp; 60 maxHeapify(data,i,0); 61 } 62 } 63 64 /** 65 *父节点位置 66 * 67 *@paramcurrent 68 *@return 69 */ 70 private static int getParentIndex(int current){ 71 return(current-1)>>1;//右移相当于除以2 72 } 73 74 /** 75 *左子节点position注意括号,加法优先级更高 76 * 77 *@paramcurrent 78 *@return 79 */ 80 private static int getChildLeftIndex(int current){ 81 return current*2+1; 82 } 83 84 /** 85 *右子节点position 86 * 87 *@paramcurrent 88 *@return 89 */ 90 private static int getChildRightIndex(int current){ 91 return current*2+2; 92 } 93 94 private static void print(int[] data){ 95 96 for(int i=0;i<data.length;i++){ 97 98 System.out.print(data[i]+" "); 99 } 100 } 101 102 103 }
标签:不用 个数 复杂 括号 左右子树 左右 先来 str return
原文地址:http://www.cnblogs.com/wyq178/p/7261039.html