标签:erp play style gen close src 思想 比较 alt
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
将待排序序列R[0...n-1]看成是n个长度为1的有序序列,将相邻的有序表成对归并,得到n/2个长度为2的有序表;将这些有序序列再次归并,得到n/4个长度为4的有序序列;如此反复进行下去,最后得到一个长度为n的有序序列。
综上可知:
归并排序其实要做两件事:
(1)“分解”——将序列每次折半划分。
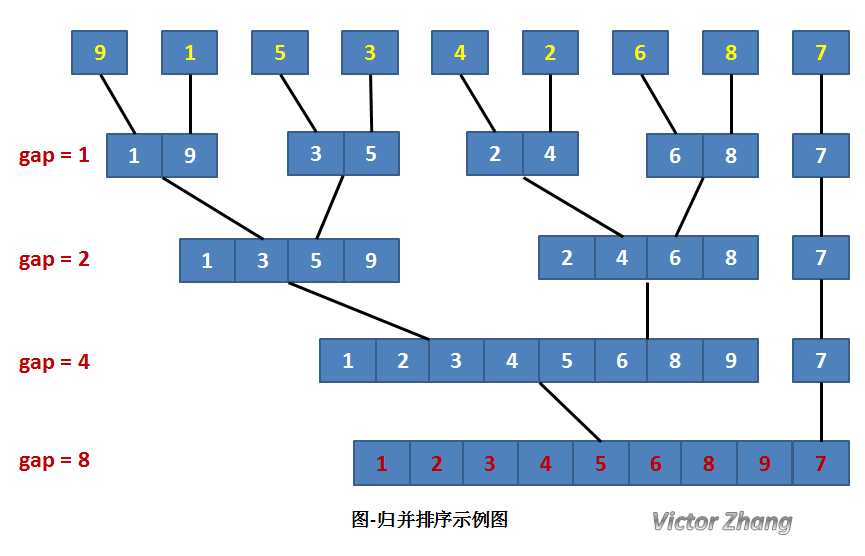
(2)“合并”——将划分后的序列段两两合并后排序。
在每次合并过程中,都是对两个有序的序列段进行合并,然后排序。
这两个有序序列段分别为 R[low, mid] 和 R[mid+1, high]。
先将他们合并到一个局部的暂存数组R2中,带合并完成后再将R2复制回R中。
为了方便描述,我们称 R[low, mid] 第一段,R[mid+1, high] 为第二段。
每次从两个段中取出一个记录进行关键字的比较,将较小者放入R2中。最后将各段中余下的部分直接复制到R2中。
经过这样的过程,R2已经是一个有序的序列,再将其复制回R中,一次合并排序就完成了。

//归并排序 public static void merSort(int[] a) { //gap两路归并中每一路长度 for(int gap=1;gap<a.length;gap=gap*2) { merPass(a,gap); } } public static void merPass(int[] a, int gap) { // TODO Auto-generated method stub int i=0; for(;i+2*gap-1<a.length;i=i+2*gap-1) { mer(a,i,i+gap-1,i+2*gap-1); } if(i+gap-1<a.length) { mer(a,i,i+gap-1,a.length-1); } } public static void mer(int[] array, int low, int mid, int high) { int i = low; // i是第一段序列的下标 int j = mid + 1; // j是第二段序列的下标 int k = 0; // k是临时存放合并序列的下标 int[] array2 = new int[high - low + 1]; // array2是临时合并序列 // 扫描第一段和第二段序列,直到有一个扫描结束 while (i <= mid && j <= high) { // 判断第一段和第二段取出的数哪个更小,将其存入合并序列,并继续向下扫描 if (array[i] <= array[j]) { array2[k] = array[i]; i++; k++; } else { array2[k] = array[j]; j++; k++; } } // 若第一段序列还没扫描完,将其全部复制到合并序列 while (i <= mid) { array2[k] = array[i]; i++; k++; } // 若第二段序列还没扫描完,将其全部复制到合并序列 while (j <= high) { array2[k] = array[j]; j++; k++; } // 将合并序列复制到原始序列中 for (k = 0, i = low; i <= high; i++, k++) { array[i] = array2[k]; } }
标签:erp play style gen close src 思想 比较 alt
原文地址:http://www.cnblogs.com/liandy0906/p/7266994.html