标签:lock 图像 solution height 作用 变化 var 计算方法 分享
图像锐化处理的作用是使灰度反差增强,从而使模糊图像变得更加清晰。图像模糊的实质就是图像受到平均运算或积分运算,因此可以对图像进行逆运算,如微分运算能够突出图像细节,使图像变得更为清晰。由于拉普拉斯是一种微分算子,它的应用可增强图像中灰度突变的区域,减弱灰度的缓慢变化区域。
因此,锐化处理可选择拉普拉斯算子对原图像进行处理,产生描述灰度突变的图像,再将拉普拉斯图像与原始图像叠加而产生锐化图像。此原理实际为卷积操作,也可以理解为一种图像变换,最常见的图像变换(image transform,即将一幅图像转变成图像数据)就是傅里叶变换(Fourier transform),即将图像转换成源图像数据的另一种表示,而卷积是大多数变换的基础。
我们可以用方程来表示这个过程。我们首先定义图像为I(x,y),核为G(x,y),
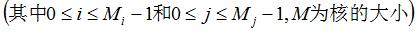
参考点位于相应核的(ai,aj)坐标上,则卷积H(x,y)定义如下:
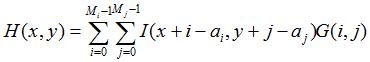
边缘部分使用复制处理,计算方法如下图所示:
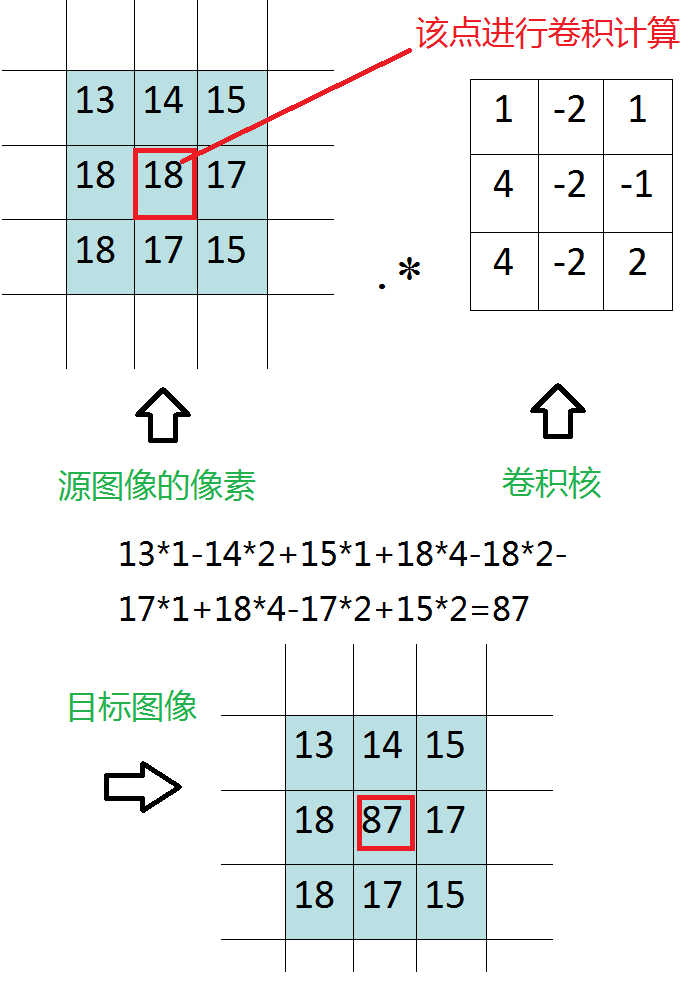
void cvFilter2D( const CvArr* src, CvArr* dst, const CvMat* kernel, CvPoint chor=cvPoint(-1,-1)); src:输入图像 dst:输出图像 kernel:卷积核, 单通道浮点矩阵. 如果想要应用不同的核于不同的通道,先用 cvSplit 函数分解图像到单个色彩通道上,然后单独处理。 anchor:核的锚点表示一个被滤波的点在核内的位置。 锚点应该处于核内部。缺省值 (-1,-1) 表示锚点在核中心。
其实在利用此卷积函数是,根据核的不同可以产生各种的图像处理,比如:
#include <iostream> #include <opencv2/highgui/highgui.hpp> #include <opencv2/core/core.hpp> #include <opencv/cv.hpp> using namespace std; using namespace cv; int main() { string picName="lena.jpg"; Mat A=imread (picName,CV_LOAD_IMAGE_COLOR); Mat mask=(Mat_<char>(3,3)<<0,-1,0, -1,5,-1, 0,-1,0); Mat B; filter2D (A,B,A.depth (),mask); imshow("A的图像",A); imshow("B的图像",B); waitKey (); return 0; }
普拉斯算子是最简单的各向同性微分算子,具有旋转不变性。一个二维图像函数 的拉普拉斯变换是各向同性的二阶导数,定义为:

在一个二维函数f(x,y)中,x,y两个方向的二阶差分分别为,
为了更适合于数字图像处理,将该方程表示为离散形式:
![]()
写成filter mask的形式如下,

注意该(a)的mask的特点,mask在上下左右四个90度的方向上结果相同,也就是说在90度方向上无方向性。为了让该mask在45度的方向上也具有该性质,对该filter mask进行扩展定义为(b)。
将Laplace算子写成filter mask后,其操作大同小异于其他的空间滤波操作。将filter mask在原图上逐行移动,然后mask中数值与其重合的像素相乘后求和,赋给与mask中心重合的像素,对图像的第一,和最后的行和列无法做上述操作的像素赋值零,就得到了拉普拉斯操作结果。
Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
src_gray,输入图像
dst,Laplace操作结果
ddepth,输出图像深度,因为输入图像一般为CV_8U,为了避免数据溢出,输出图像深度应该设置为CV_16S
kernel_size,filter mask的规模,我们的mask时3x3的,所以这里应该设置为3
scale,delta,BORDER_DEFAULT,默认设置就好//load the Original Image and get some informations Mat src = imread("012.jpg",0); namedWindow("OriginalImage"); imshow("OriginalImage",src); CV_Assert(src.depth() == CV_8U); //OpenCV solution - Laplacian Mat dst,abs_dst_laplace; Laplacian(src,dst,CV_16S,3); convertScaleAbs(dst,abs_dst_laplace); //show the result namedWindow("result_laplacian"); imshow("result_laplacian",abs_dst_laplace);


上图中上图为原图像,有图为拉普拉斯之后的图像。
标签:lock 图像 solution height 作用 变化 var 计算方法 分享
原文地址:http://www.cnblogs.com/polly333/p/7269843.html