标签:影响 get label ted oci archive env analysis 打开
本文主要总结近期学习的Social Network Analysis(SNA)中的各种Centrality度量,我暂且翻译为中心度。本文主要是实战,理论方面几乎没有,因为对于庞大的SNA,我可能连门都没有入,但是我觉得这不影响我理解原理后使用他们。
本文为原创,如有不小心侵权的问题出现,请联系本人删除。本文不允许任何形式的转载!!!
一、Centrality的定义
在SNA领域的centrality是用于衡量图中节点的重要度,不同的centrlity算法会对同一节点给出差异很大的centrality。如Wikipedia中的这幅图。
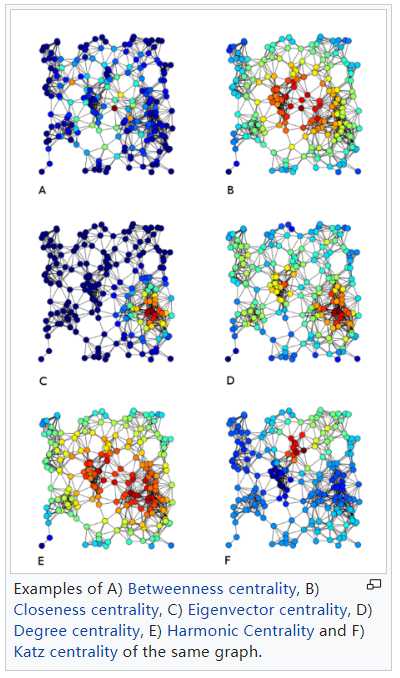
图片链接:https://en.wikipedia.org/wiki/Centrality
二、Centrality的相关资源
1. wiki: https://en.wikipedia.org/wiki/Centrality
2. ttang pageRank networkx: http://www.cnblogs.com/fstang/archive/2013/06/01/3113352.html
3. 讲network的一个网站:https://www.sci.unich.it/~francesc/teaching/network/
4. 各种语言的centrality代码资源集合: http://www.centiserver.org/?q1=software
三、Networkx中的EigenCentrality, PageRank和KatzCentrality的对比
本文主要考察的是EigenCentrality, PageRank和KatzCentrality之间的区别和联系。PageRank广为人知,是Google对网页排序的基础方法之一。其实Google的PageRank和KatzCentrality都是EigenCentrality的变形。
EigenCentrality的基本思想跟google是一样的,都是认为与得分(centrality)高的点相连的点更加重要。EigenCentrality就是用图的邻接矩阵来计算EigenCentrality(engenvector centrality, 特征向量中心度)。具体的公式和推到可以参考上面给出的维基百科链接,代码实现可以参考networkx,还有https://www.sci.unich.it/~francesc/teaching/network/,但是我打开页面,里面的公式显示有问题,这个网站的解释非常的简洁明了,适合入门,还有R代码和相应的图演示。
参考ttang的博客,我做了EigenCentrality, PageRank和KatzCentrality的对比,在此表示由衷的感谢。ttang的pageRank实现代码参考链接:
http://www.cnblogs.com/fstang/archive/2013/06/01/3113352.html
下面是本文的代码实现:
1 import matplotlib.pyplot as plt 2 import networkx as nx 3 4 G=nx.binomial_graph(10, 0.3, directed=True) #the graph 5 G.add_node(10); # add a sole node 6 layout = nx.spring_layout(G) 7 8 plt.figure("source graph") 9 nx.draw(G, pos=layout, node_color=‘y‘) 10 11 plt.figure("eigenCentrality without personalization") 12 pr=nx.eigenvector_centrality(G) 13 print("eigenCentrality without personalization" ,pr) 14 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 15 16 plt.figure("eigenCentrality with personalization") 17 pr=nx.eigenvector_centrality(G, nstart={0:1, 1:1, 2:10, 3:1, 4:1, 5:1, 6:1, 7:1, 8:1, 9:1, 10:1}) 18 print("eigenCentrality with personalization" ,pr) 19 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 20 21 plt.figure("pageRank without personalization") 22 pr=nx.pagerank(G,alpha=0.85) 23 print("pageRank without personallization", pr) 24 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 25 26 plt.figure("pageRank with personalization ") 27 pr=nx.pagerank(G,alpha=0.85, personalization={0:1, 1:1, 2:10, 3:1, 4:1, 5:1, 6:1, 7:1, 8:1, 9:1, 10:1}) 28 print("pageRank with personalization" , pr) 29 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 30 31 plt.figure("katzcentrality without personalization") 32 pr=nx.katz_centrality(G, alpha=0.3); 33 print("katzcentrality without personallization ", pr) 34 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 35 36 plt.figure("katzcentrality with personalization") 37 pr=nx.katz_centrality(G,alpha=0.3, nstart={0:1, 1:1, 2:10, 3:1, 4:1, 5:1, 6:1, 7:1, 8:1, 9:1, 10:1}) 38 print("katzcentrality with personalization" , pr) 39 nx.draw(G, pos=layout, node_size=[x * 6000 for x in pr.values()],node_color=‘m‘,with_labels=True) 40 plt.show()
这是画出来的图,自己跑一下看得清楚写,这里贴出来的图只是示意。
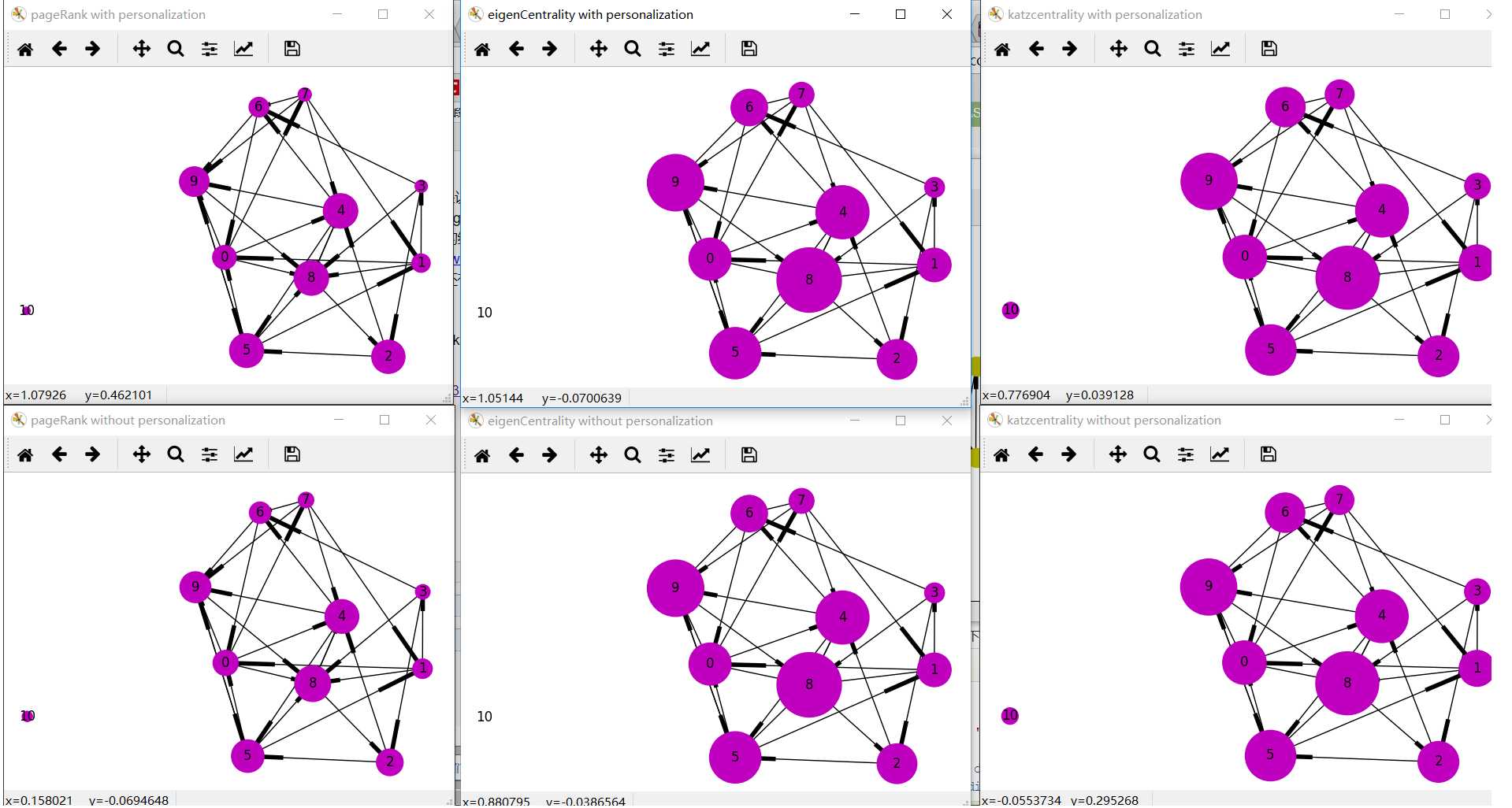
最左边一列是pageRank有无personalization,也就是节点预先设定的重要度的对比情况;
中间一列是eigenCentrality有无personalization的对比;
右边一列是katzCentrality有无personalization的对比。
上次我看这个图的时候,觉得节点预设重要度对pageRank算法的影响很小,对katzCentrality的影响比较大,不过今天看,感觉好像都差不多。
由于节点10没有边与其它节点相连,有没有pageRank的转移概率,有没有katzCentrality的beta,因此节点10在eigenCentrality里centrality为0.
Social Network Analysis的Centrality总结,以及networkx实现EigenCentrality,PageRank和KatzCentrality的对比
标签:影响 get label ted oci archive env analysis 打开
原文地址:http://www.cnblogs.com/yucaodie/p/7282803.html