标签:不能 意图 下标 -- ima 并且 images bst 最小堆
转载请注明源出处:http://www.cnblogs.com/lighten/p/7299233.html
本章介绍队列中的PriorityQueue--优先队列,顾名思义,这是一个可以指定特定排序的队列。有些违背队列的先入先出,但是其是按照有序的出队列,也是一个比较实用的类。
PriorityQueue继承自抽象父类AbstractQueue,其数据结构依旧保持简单:
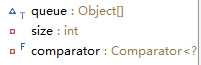
一个数组队列,一个大小,一个排序规则的比较器。如果比较器为null的时候,就按照元素自身的compareTo方法进行比较排序。这个队列和之前容器又在初始化的大小和扩容大小上不一致,其默认大小为11,大小小于64的时候扩容后为原来的3倍,大于64的时候,扩容后打下是原来的2倍。

PriorityQueue的add(E)方法和offer(E)方法是一样的。

先判断容量大小,再判断是否是第一个,最后进行排序。
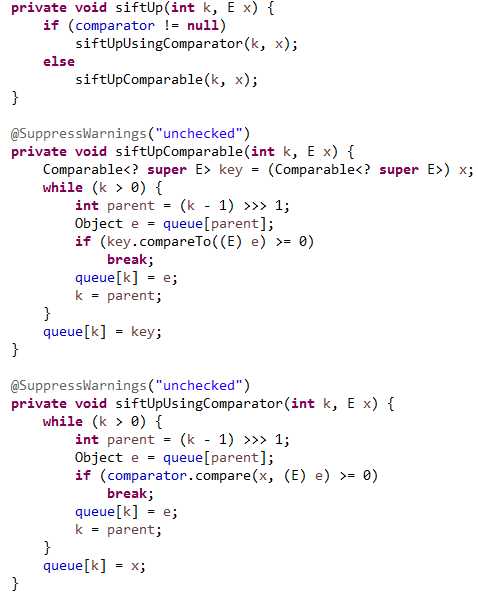
这个排序看过去有些奇怪,怎么有parent,并且下标是(k-1)>>>1呢?其实这里的操作就反应了优先队列的真正数据结构,其实际上是一个二叉树,将二叉树存储在数组之中而已。根节点就是数组的0位。下图给出其具体结构:
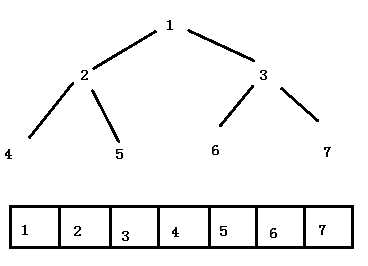
上图就是随手画的一个二叉树,下面是对应的二叉树的数组中的位置。二叉树存入数组的方式很简单,就是从上到下,从左到右。PriorityQueue的是一个有特点的完全二叉树,且不允许出现null节点,其父节点都比叶子节点小,这个是堆排序中的小顶堆。如果按数组顺序我们可以得到如下结论:
左叶子节点=父节点下标*2+1
右叶子节点=父节点下标*2+2
父节点=(叶子节点-1)/2
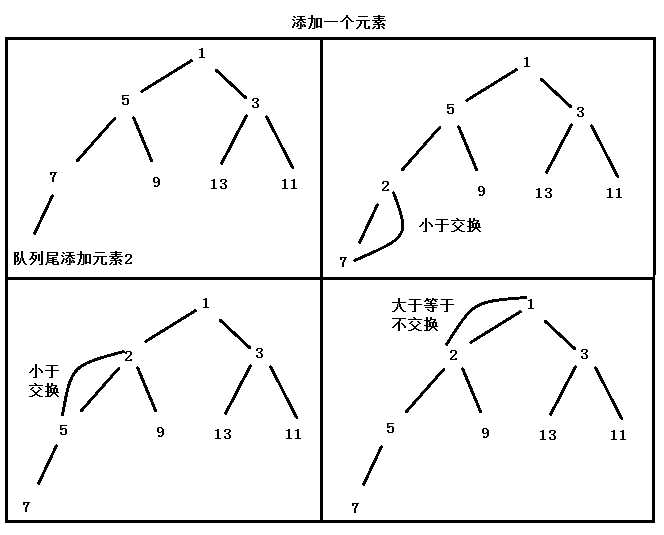
插入节点也就比较好处理了,和父节点比较,大于父节点的就不动,小于父节点的就上浮,这就是siftUp方法的作用了。顺便一提,最小堆并不保证左右节点的大小关系,只关心父节点和子节点的关系。
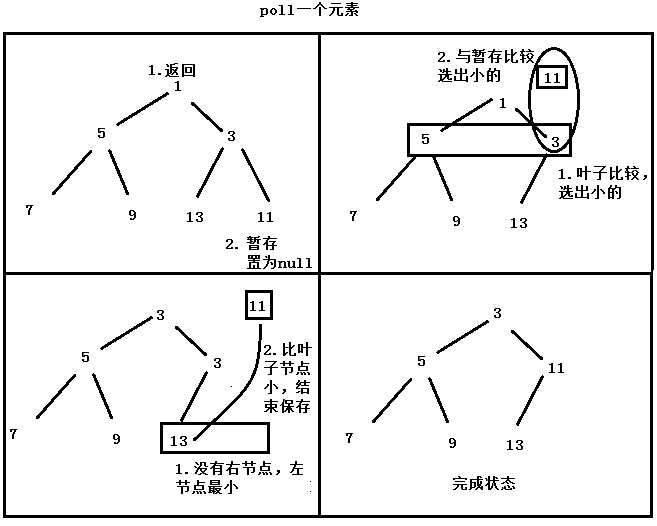
由上面的叙述,不难看出优先队列如果不进行调整,是无法保证优先顺序的,子节点大小是无序的。所以每次出队列的都是根元素,根元素肯定是最小的。移除了一个元素后,树的结构势必会被破坏,所以每次的移除操作都会调整树,保证其符合定义。

siftDown就是用于做这样的调整的,其具体实现如下:

看代码就可以知道,其移除节点之后,是判断了左右节点小的那个进行上浮的,而后循环上浮。

移除任意一个位置的内容时,其是将最后一个元素取出来变成null了。然后调用siftDown,重新找到最后一个元素应该去的位置,其它元素填补移除位。一般而言这样就应该足够了,但是在某些情况下还需要进行后面的元素与前面进行交换。就像代码中所表现的一样,最后一个元素正好填补的是移除的那个空缺,此种情况下并不能说明该结构是正确的,造成这种现象的原因就在于优先队列并不保证左右的大小顺序,看下图就能很好理解问题所在,并且此种情况需要进行siftUp(),当发生这种异常的情况,才会返回这个异常值,其它时候都是返回null.
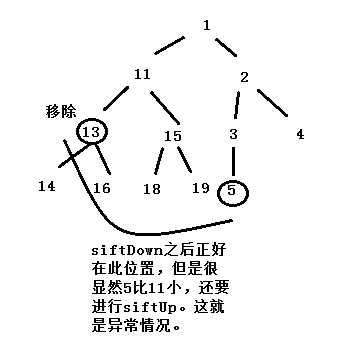
移除任意位置的图就不再给出了,2小结结尾已经进行过说明,先进行一次siftDown,再进行一次siftUp。
http://www.cnblogs.com/CarpenterLee/p/5488070.html
标签:不能 意图 下标 -- ima 并且 images bst 最小堆
原文地址:http://www.cnblogs.com/lighten/p/7299233.html