标签:连通 tac 输出 ack oid 一个 cst pop 删掉
有n个同学(编号为1到n)正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息,但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入格式:
输入共2行。
第1行包含1个正整数n表示n个人。
第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i的同学的信息传递对象是编号为Ti的同学,Ti≤n且Ti≠i
数据保证游戏一定会结束。
输出格式:
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
5 2 4 2 3 1
3
样例1解释
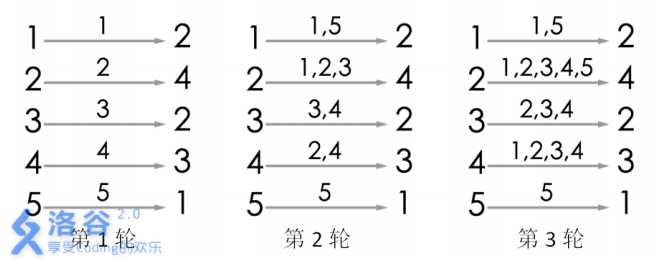
游戏的流程如图所示。当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自
己的生日,所以答案为 3。当然,第 3 轮游戏后, 2 号玩家、 3 号玩家都能从自己的消息
来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
很明显,这道题可以转换为图论中求最小环的问题。
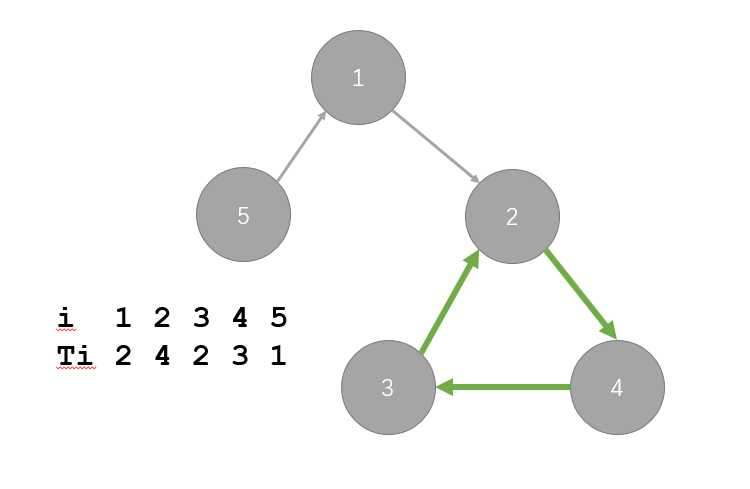
(本来还找了一下画图论的图的软件,后来发现PPT的功能已经足够强大= =)
把每个同学当做节点,i和Ti之间连有向边。
去年刷到这道题时一直觉得环的特征不明显,今年对图论理解深刻了点,就好些了……
求环就有很多种方式咯,在这里说两种。
拓扑排序时会不断删掉入度为0的点,然而环中的点入度永远不会为0,于是环被保留了下来。
凭借这个性质搜索剩下的环中最小的长度。
因为每同学都只有一位固定对象,所以每个节点出度都为1。此时求强连通分量等同于求环。
傻X错误:这张图可能不连通!比如:
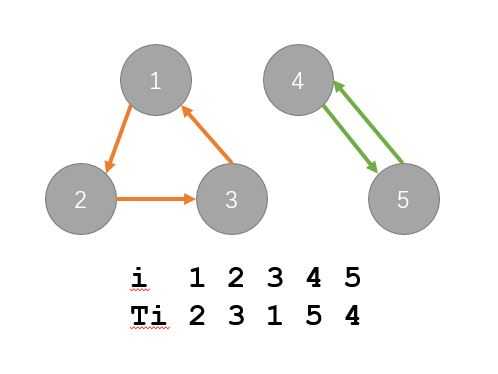
所以需要循环tarjan...o(╯□╰)o
方法一:

1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<algorithm> 5 using namespace std; 6 int n; 7 int ans=10000000; 8 struct node 9 { 10 int next; 11 int cnt; 12 bool bj; 13 node(){next=0;cnt=0;bj=0;} 14 }a[200001]; 15 queue <node> que; 16 int main() 17 { 18 cin>>n; 19 for(int i=1;i<=n;i++) 20 { 21 cin>>a[i].next; 22 a[a[i].next].cnt++;//记录入度 23 } 24 //拓扑 25 for(int i=1;i<=n;i++) 26 { 27 if(a[i].cnt == 0) 28 { 29 que.push(a[i]); 30 a[i].bj=1; 31 } 32 } 33 while(!que.empty()) 34 { 35 node i=que.front(); 36 que.pop(); 37 if(--a[i.next].cnt==0) 38 { 39 que.push(a[i.next]); 40 a[i.next].bj=1; 41 } 42 } 43 44 for(int i=1;i<=n;i++) 45 { 46 if(a[i].bj==0) 47 { 48 int j=i,count=0; 49 do 50 { 51 count++; 52 a[j].bj=1; 53 j=a[j].next; 54 }while(j!=i); 55 ans=min(ans,count); 56 } 57 } 58 cout<<ans; 59 return 0; 60 }
方法二:

1 /* 2 */ 3 #include<iostream> 4 #include<cstdio> 5 #include<cstring> 6 #include<vector> 7 using namespace std; 8 9 int n,scc=0,idx=0,s[200700],low[200700],dfn[200700],top=0; 10 bool in_stack[200700]; 11 int ans=10000000; 12 vector<int> edge[200700]; 13 int length[200700]; 14 15 void tarjan(int u) { 16 dfn[u] = low[u] = ++idx;//init 17 s[top++] = u;//压栈 18 in_stack[u] = true; 19 for (int i = 0; i < edge[u].size();i++) { 20 int v = edge[u][i]; 21 if (!dfn[v]) {//未被访问过 22 tarjan(v);//continue 23 low[u] = min(low[u], low[v]); 24 } 25 else if (in_stack[v]) {//如果还在栈内 26 low[u] = min(low[u], dfn[v]); 27 } 28 } 29 int size=0; 30 if (dfn[u] == low[u]) {//如果u是强联通的根 31 do { 32 size++; 33 in_stack[s[--top]] = false;//退栈 34 } while (s[top] != u);//走完一个环返回 35 if(size != 1) 36 ans=min(ans,size); 37 } 38 } 39 int main(){ 40 scanf("%d",&n); 41 for(int i=1;i<=n;i++){ 42 int v; 43 scanf("%d",&v); 44 edge[i].push_back(v); 45 } 46 for(int i=1;i<=n;i++) 47 tarjan(i); 48 printf("%d",ans); 49 return 0; 50 }
标签:连通 tac 输出 ack oid 一个 cst pop 删掉
原文地址:http://www.cnblogs.com/monkeytu/p/7309476.html