标签:str 迭代 时间复杂度 开发 n+1 指针 解释 alt detection
Floyd判圈算法(Floyd Cycle Detection Algorithm),又称龟兔赛跑算法(Tortoise and Hare Algorithm),是一个可以在有限状态机、迭代函数或者链表上判断是否存在环,求出该环的起点与长度的算法。该算法据高德纳称由美国科学家罗伯特·弗洛伊德发明,但这一算法并没有出现在罗伯特·弗洛伊德公开发表的著作中。
如果有限状态机、迭代函数或者链表上存在环,那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇。同时显然地,如果从同一个起点(即使这个起点不在某个环上)同时开始以不同速度前进的2个指针最终相遇,那么可以判定存在一个环,且可以求出2者相遇处所在的环的起点与长度。
判断是否存在环路:
如果有限状态机、迭代函数或者链表存在环,那么一定存在一个起点可以到达某个环的某处(这个起点也可以在某个环上)。
初始状态下,假设已知某个起点节点为节点S。现设两个指针t和h,将它们均指向S。接着,同时让t和h往前推进,但是二者的速度不同:t每前进1步,h前进2步。只要二者都可以前进而且没有相遇,就如此保持二者的推进。当h无法前进,即到达某个没有后继的节点时,就可以确定从S出发不会遇到环。反之当t与h再次相遇时,就可以确定从S出发一定会进入某个环,设其为环C。如果确定了存在某个环,就可以求此环的起点与长度。
求解环路的长度:
上述算法刚判断出存在环C时,显然t和h位于同一节点,设其为节点M。显然,仅需令h不动,而t不断推进,最终又会返回节点M,统计这一次t推进的步数,显然这就是环C的长度。
求解环路的起点:
为了求出环C的起点,只要令h仍均位于节点M,而令t返回起点节点S,此时h与t之间距为环C长度的整数倍。随后,同时让t和h往前推进,且保持二者的速度相同:t每前进1步,h前进1步。持续该过程直至t与h再一次相遇,设此次相遇时位于同一节点P,则节点P即为从节点S出发所到达的环C的第一个节点,即环C的一个起点。
对于环路起点算法的解释:
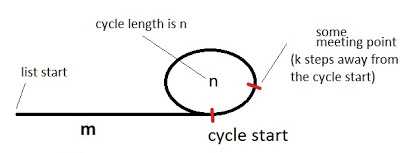
假设出发起点到环起点的距离为m,已经确定有环,环的周长为n,(第一次)相遇点距离环的起点的距离是k。那么当两者相遇时,慢指针(t)移动的总距离i = m + a * n + k,快指针(h)的移动距离为2i,2i = m + b * n + k。其中,a和b分别为t和h在第一次相遇时转过的圈数。让两者相减(快减慢),那么有i = (b - a) * n。即i是圈长度的倍数。
将一个指针移到出发起点S,另一个指针仍呆在相遇节点M处两者同时移动,每次移动一步。当第一个指针前进了m,即到达环起点时,另一个指针距离链表起点为i + m。考虑到i为圈长度的倍数,可以理解为指针从链表起点出发,走到环起点,然后绕环转了几圈,所以第二个指针也必然在环的起点。即两者相遇点就是环的起点。
t := &S
h := &S //令指针t和h均指向起点节点S。
repeat
t := t->next
h := h->next
if h is not NULL //要注意这一判断一般不能省略
h := h->next
until t = h or h = NULL
if h != NULL //如果存在环的话
n := 0
repeat //求环的长度
t := t->next
n := n+1
until t = h
t := &S //求环的一个起点
while t != h
t := t->next
h := h->next
P := *t
时间复杂度:注意到当指针t到达环C的一个起点节点P时(此时指针h显然在环C上),之后指针t最多仅可能走1圈。若设节点S到P距离为 m,环C的长度为 n,则时间复杂度为 O(m+n),是线性时间的算法。
空间复杂度:仅需要创立指针t、指针h,保存环长n、环的一个起点P。空间复杂度为 O(1),是常数空间的算法。
标签:str 迭代 时间复杂度 开发 n+1 指针 解释 alt detection
原文地址:http://www.cnblogs.com/zzy19961112/p/7355369.html