标签:.net ica font length 矩阵 个数 tin 聚类分析 bsp
1965年美国加州大学柏克莱分校的扎德教授第一次提出了‘集合’的概念。经过十多年的发展,模糊集合理论渐渐被应用到各个实际应用方面。为克服非此即彼的分类缺点,出现了以模糊集合论为数学基础的聚类分析。用模糊数学的方法进行聚类分析,就是模糊聚类分析。FCM(Fuzzy C-Means)算法是一种以隶属度来确定每个数据点属于某个聚类程度的算法。该聚类算法是传统硬聚类算法的一种改进。
算法流程:
优点:相比起前面的”硬聚类“,FCM方法会计算每个样本对所有类的隶属度,这给了我们一个参考该样本分类结果可靠性的计算方法,若某样本对某类的隶属度在所有类的隶属度中具有绝对优势,则该样本分到这个类是一个十分保险的做法,反之若该样本在所有类的隶属度相对平均,则我们需要其他辅助手段来进行分类。
缺点:KNN的缺点基本它都有
模糊聚类
cluster::fanny
需要R安装包
install.packages("cluster")
示例代码:
library(cluster) iris2 <- iris[-5] fannyz=fanny(iris2,3,metric="SqEuclidean")
summary(fannyz)
分类分布:
> fannyz$clustering
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 2 3 3 3 3 3 3 3 3 3 3 3 3
[66] 3 3 3 3 3 3 3 3 3 3 3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 3 2 2 2 2 3 2 2 2 2 2 2 3 2 2 2 2 2 3 2 3 2 3 2 2 3 3 2 2
[131] 2 2 2 3 2 2 2 2 3 2 2 2 3 2 2 2 3 2 2 3
样本隶属度
> fannyz$membership
[,1] [,2] [,3]
[1,] 0.996623586 0.0010720343 0.0023043797
[2,] 0.975852543 0.0074979471 0.0166495094
[3,] 0.979825922 0.0064145785 0.0137594999
[4,] 0.967427446 0.0101075228 0.0224650314
[5,] 0.994470355 0.0017679352 0.0037617094
[6,] 0.934574112 0.0206196544 0.0448062334
[7,] 0.979491667 0.0065045178 0.0140038150
[8,] 0.999547263 0.0001412048 0.0003115325
[9,] 0.930379787 0.0219024180 0.0477177955
.......
图示显示 :clusplot(fannyz)
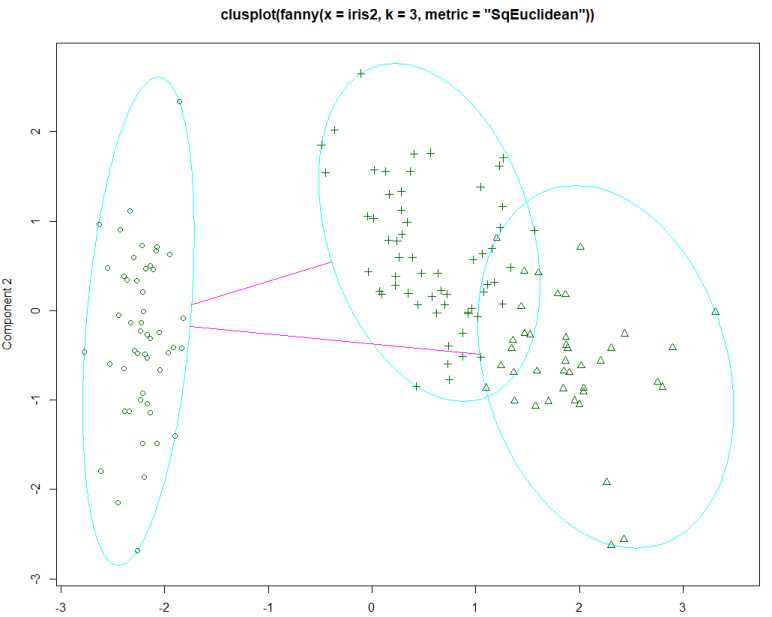
结果显示
> table(iris$Species,fannyz$clustering)
1 2 3
setosa 50 0 0
versicolor 0 3 47
virginica 0 37 13
e1071::cmeans
安装包代码:
install.packages("e1071")
示例代码:
> library("e1071")
> x <- iris[-5]
> result1<-cmeans(x,3,50)
> result1
Fuzzy c-means clustering with 3 clusters
Cluster centers:
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.888999 2.761093 4.364049 1.3973654
2 6.775092 3.052406 5.646882 2.0535855
3 5.003966 3.414086 1.482821 0.2535487
Memberships:
1 2 3
[1,] 0.0023043721 0.0010720485 0.996623579
[2,] 0.0166481906 0.0074975084 0.975854301
[3,] 0.0137586391 0.0064142953 0.979827066
.......
统计结果:
> table(iris$Species,result1$cluster)
1 2 3
setosa 0 0 50
versicolor 47 3 0
virginica 13 37 0
3d效果显示示例
#install.packages("scatterplot3d")
library(scatterplot3d)
scatterplot3d(result1$membership, color=result1$cluster, type="h",
angle=55, scale.y=0.7, pch=16, main="Pertinence")
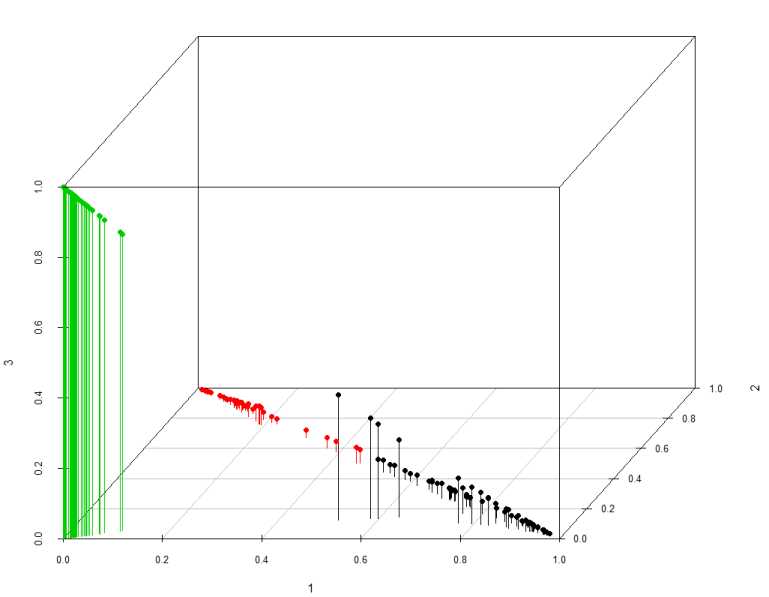
参考资料:
标签:.net ica font length 矩阵 个数 tin 聚类分析 bsp
原文地址:http://www.cnblogs.com/tgzhu/p/7326520.html