标签:str sharp 答案 其他 har .com a算法 i++ com
图片素材借鉴啊哈磊的博客
该算法用于解决一个点到其余各顶点的最短路径
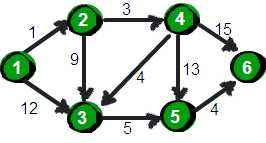
先来一张图,求1点到6点的最短路径
这让我想起了差点挂科的运筹学
先用一个二维数组
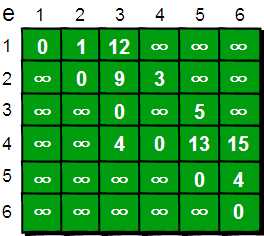
还有一个一维数组存储1点到各点的距离

这个一维数组的值称为估计值。在1点可直接到达的点中选择一个最近的点,即点2.然后点2的值也就成为了确定值。
why。因为路径是正数,也不可能通过其他的中转点缩短点1到点2的路程。
经过了点2,再看看点2能够到达哪些点。即点3和点4。先讨论下通过点2这个中转点是否能够缩短点1到点3的路程。答案是可以的。1+9<12.修改一维数组对应的值。
这个就叫松弛
同理比较点1到点4距离和通过点2中转的距离。
剩下的3,4,5,6点自己试试。不然运筹学很容易挂的
最后答案是

贴出核心算法
for(i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
min=inf;//初始min为正无穷
for(j=1;j<=n;j++)
{
if(book[j]==0 && dis[j]<min)
{
min=dis[j];//取得离源点直接相连的最近的点的距离
u=j;
}
}
book[u]=1;//将该点纳入已经确定要走的点的集合
for(v=1;v<=n;v++)//这里就如同遍历哥各点到点2的距离
{
if(e[u][v]<inf)
{
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
标签:str sharp 答案 其他 har .com a算法 i++ com
原文地址:http://www.cnblogs.com/dailinfu/p/7398112.html