标签:width bool bin 顺序 最小 有一个 most nim 没有
首先是当年stoer和wagner两位大佬发表的关于这个算法的论文:A Simple Min-Cut Algorithm
直接上算法部分:
分割线 begin

在这整篇论文中,我们假设一个普通无向图G=(V,E),其中每条边e都有一个正实数权值w(e)。
如果我们知道:怎样找到两个节点s,t,以及怎样得到对于s-t的最小割,我们就几乎解决了整个问题:
定理2.1:
设s和t是图G中的两个节点,设G/{s,t}是合并s和t后得到的图,
则图G的全局最小割可以通过“图G对于s-t的最小割”和“图G/{s,t}的全局最小割”得到。

定理说明:
若图G存在一个全局最小割,使得s和t被分割,那么,图G的s-t最小割就等于图G的全局最小割。
否则(即全局最小割没有分割s和t),图G的全局最小割就等于图G/{s,t}的全局最小割。
因此,我们可以使用一个寻找任意s-t最小割的程序来构建一个递归算法,从而寻找一个图的全局最小割。
下面的算法(使用一些骚操作搜索方法),可以产生我们想得到的s-t最小割。
MinimumCutPhase(G,w,a) //分阶段(phase),每个阶段都产生相应的当前阶段最小割
{
A←{a}
while( A ≠ V )
{
选取“最紧密相连的点”加入A
}
记录当前阶段的割,并且合并最后加入的两个点
}
呵,听起来就很玄乎,什么玩意儿呢,下面有解释。

A是作为V的一个子集,开始时是空集,我们任取一个点,加入到A中,然后通过某个规则不断地往A中加入点,直到A == V为止,那是什么规则呢?
在每一步的加点操作中,我们选择集合(V - A)中和A“最紧密相连的点”加入A,那什么是“最紧密相连的点”呢?
设:点y∈ V - A ,且点y为与集合A直接相连的点,所有点y的集合为Y;
所有与集合A直接相连的边的权重总和为w(A,y);
则:“最紧密相连的点” z 满足: z ∈ Y,并且w(A,z)为所有w(A,y)中最大的。
通俗的说,就是V - A集合里,找一个直接与A相连的点,这个点是 Σ(该点所有与A直接相连的边的权值) 最大的那个。
(不难看出,这是一种类似于prim算法生成类似最大生成树的算法)
在我们不断往A加点的过程中,记录下最后加入A的两个点,记为s和t,对这两个点进行合并操作(merge):
删除点s和点t,加入新的点u作为代替,所有原本从s或t点出发的边(edge< s , t >除外,这条边删除;并且设这些边到达的点为x),都用一条新的edge< u , x >代替;
并且 edge< u , x >.weight = edge< s , x >.weight + edge< t , x >.weight ; (若某条边不存在,则定义其weight=0)
(当然需要注意的是,所有讨论都是建立在无向图上,故这里的出发、到达不代表这条边的方向,只是单纯描述该边的两个端点)
然后,我们把当前分割s和t的割(cut),叫做阶段割(the-cut-of-phase),不难得到,阶段割等于w(A,t) (注意,此处的集合A表示加入点t前的集合A);
then,所有阶段割中最小的,即本算法的结果,即我们想求的全局最小割。
MinimumCut(G,w,a)
{
while(|V| > 1)
{
MinimumCutPhase(G,w,a)
if(阶段割 < 当前全局最小割) 当前全局最小割 = 阶段割
}
}
最后,注意到节点a在本算法整个过程中是一直不变的,实际上它也可以在每个阶段(phase)进行任意选择。
分割线 end
然后是论文中的example部分:
分割线 begin
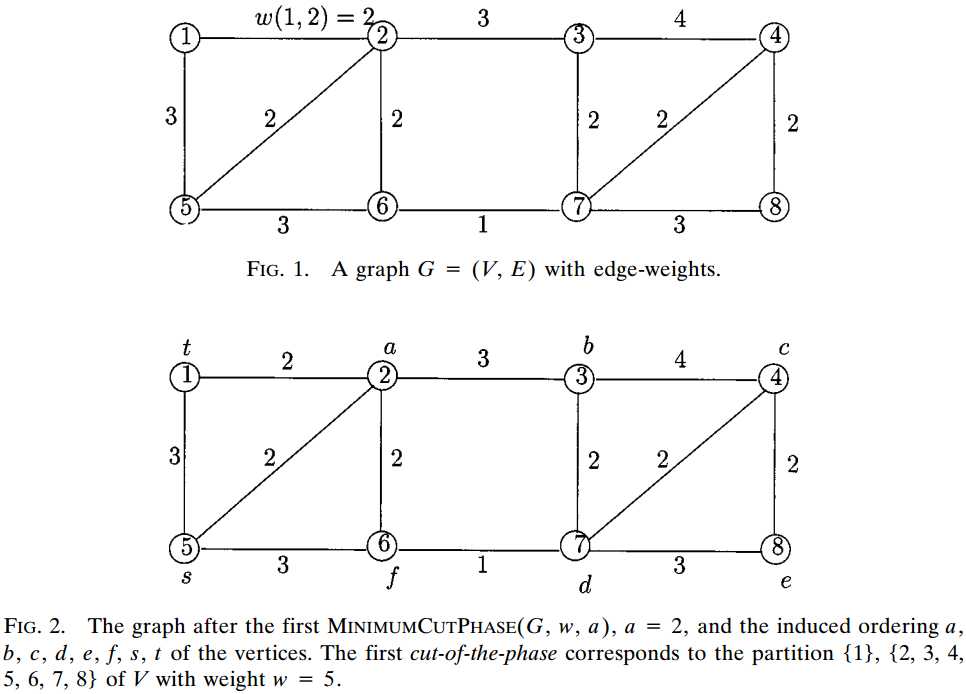
这是第一次MinimumCutPhase(G,w,a)操作前和操作后的样子,
在此次MinimumCutPhase(G,w,a)操作中,进入集合A的点的顺序为: 2 → 3 → 4 → 7 → 8 → 6 → 5(s) → 1(t) ;
显然,此次的阶段割cut-of-the-phase.weight = w(A,t) = edge<1,2>.w + edge<1,5>.w = 5 ;
之后的操作与此类似,不再赘述,可以自行对照论文中的FIG。
分割线 end
当然,上stoer和wagner两位巨老当初的论文,装逼成分多余实际效用= =,感觉自己翻译也翻译的像一坨shit一样;
更多细节更深理解还请看中文:http://files.cnblogs.com/files/dilthey/stoer-wagner%E7%AE%97%E6%B3%95.pdf
算法模板:
1 #define MAXN 500+5 2 #define INF 0x3f3f3f3f 3 int n;//1~n共n个点 4 int edge[MAXN][MAXN],dist[MAXN]; 5 bool vis[MAXN],bin[MAXN]; 6 void init() 7 { 8 memset(edge,0,sizeof(edge)); 9 memset(bin,0,sizeof(bin)); 10 } 11 void addedge(u,v,w) 12 { 13 edge[u][v]=w; 14 edge[v][u]=w; 15 } 16 int merge(int &s,int &t)//对应论文中的MinimumCutPhase() 17 { 18 memset(dist,0,sizeof(dist)); 19 memset(vis,0,sizeof(vis)); 20 int k,mincut,maxc; 21 for(int i=1;i<=n;i++) 22 { 23 k=-1, maxc=-1; 24 for(int j=1;j<=n;j++) if(!bin[j] && !vis[j] && dist[j] > maxc) {k=j;maxc=dist[j];} 25 //寻找"the most tightly connected vertex" 26 if(k == -1) return mincut; 27 vis[k]=true;//点k加入集合A 28 s=t; t=k;//不断移动s和t,保证他们是最后进入集合A的两个点 29 mincut=maxc;//不断更新mincut为w(A,t) 30 for(int j=1;j<=n;j++) if(!bin[j] && !vis[j]) dist[j]+=edge[k][j];//计算所有的w(A,y) 31 } 32 return mincut; 33 } 34 int stoer_wagner() 35 { 36 int mincut=INF,s,t,ans; 37 for(int i=1;i<=n-1;i++)//merge(s,t)一次减少一个点,|V|要从n减少到1,故要进行n-1次 38 { 39 ans=merge(s,t); 40 bin[t]=1;//把t合并到s中 41 if(ans<mincut) mincut=ans; 42 if(mincut==0) return 0; 43 for(int j=1;j<=n;j++) if(!bin[j]) edge[s][j]=(edge[j][s]+=edge[j][t]);//更新所有从s出发的边 44 } 45 return mincut; 46 }
标签:width bool bin 顺序 最小 有一个 most nim 没有
原文地址:http://www.cnblogs.com/dilthey/p/7399281.html