ML: 降维算法-PCA

标签：根据   cti   matrix   standard   卡尔   数据分析   很多   协方差矩阵   日期   

        PCA (Principal Component Analysis) 主成份分析 也称为卡尔胡宁-勒夫变换（Karhunen-Loeve Transform），是一种用于探索高维数据结构的技术。PCA通常用于高维数据集的探索与可视化。还可以用于数据压缩，数据预处理等。PCA可以把可能具有相关性的高维变量合成线性无关的低维变量，称为主成分（ principal components）。新的低维数据集会尽可能的保留原始数据的变量。PCA将数据投射到一个低维子空间实现降维。例如，二维数据集降维就是把点投射成一条线，数据集的每个样本都可以用一个值表示，不需要两个值。三维数据集可以降成二维，就是把变量映射成一个平面。一般情况下，n 维数据集可以通过映射降成k 维子空间。

目录：

• 降维问题
• stats::princomp
• stats::prcomp
• 其它R包

数据的向量表示及降维问题

       在数据挖掘和机器学习中，数据被表示为向量。例记录每天商品交易的数据记录，格式如下：

• (日期, 浏览量, 访客数, 下单数, 成交数, 成交金额)

      其中“日期”是一个记录标志而非度量值，而数据挖掘关心的大多是度量值，因此如果我们忽略日期这个字段后，我们得到一组记录，每条记录可以被表示为一个五维向量，其中一条看起来大约是这个样子：

• (500,240,25,13,2312.15)^\mathsf{T}

     当然可以对这一组五维向量进行分析和挖掘，不过我们知道，很多机器学习算法的复杂度和数据的维数有着密切关系，甚至与维数呈指数级关联。当然，这里区区五维的数据，也许还无所谓，但是实际机器学习中处理成千上万甚至几十万维的情况也并不罕见，在这种情况下，机器学习的资源消耗是不可接受的，因此必须对数据进行降维。降维当然意味着信息的丢失，不过鉴于实际数据本身常常存在的相关性，可以想办法在降维的同时将信息的损失尽量降低。     

    从上面的交易示例数据，从经验可以知道，“浏览量”和“访客数”往往具有较强的相关关系，而“下单数”和“成交数”也具有较强的相关关系。我们可以直观理解为“当某一天的浏览量较高（或较低）时，我们应该很大程度上认为这天的访客数也较高（或较低）”。这种情况表明，如果删除浏览量或访客数其中一个指标，我们应该期待并不会丢失太多信息。因此我们可以删除一个，以降低机器学习算法的复杂度。上面给出的是降维的朴素思想描述，可以有助于直观理解降维的动机和可行性，但并不具有操作指导意义。例如，我们到底删除哪一列损失的信息才最小？亦或根本不是单纯删除几列，而是通过某些变换将原始数据变为更少的列但又使得丢失的信息最小？到底如何度量丢失信息的多少？如何根据原始数据决定具体的降维操作步骤？

    PCA是一种具有严格数学基础并且已被广泛采用的降维方法。对于PCA的原理及算法推演可参考如下资料：

• http://blog.jobbole.com/109015/
• http://www.360doc.com/content/13/1124/02/9482_331688889.shtml

     PCA算法主要分为6个步骤：

1. 构建p*n阶的变量矩阵
2. 将p*n阶的变量矩阵X的每一行（代表一个属性字段）进行标准化
3. 求出协方差矩阵C
4. 求出协方差矩阵的特征值及对应的特征向量
5. 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k列组成矩阵P
6. Y=XP即为降维到k维后的数据

stats::princomp

   Usage : princomp(x, cor = FALSE, scores = TRUE,  ...)

• cor :  逻辑值，TRUE：表示使用相关矩阵求主成分、False: 使用协方差矩阵求主成分
• scores:  逻辑值，该值指示是否计算主成分得分

      返回值

• loadings 是一个矩阵，每列是一个特征向量，即原始特征的旋转系数
• scores   所提供的数据在各个主成分上的得分

  其它函数：

• #princomp()主成分分析   可以从相关阵或者从协方差阵做主成分分析
• #summary()提取主成分信息
• #loadings()显示主成分分析或因子分析中载荷的内容
• #predict()预测主成分的值，predict(object，newdata，…)：#object是由prcomp()得到的对象，newdata是由预测值构成的数据框，当newdata缺省时，预测已有数据的主成分值
• #screeplot()画出主成分的碎石图
• #biplot()画出数据关于主成分的散点图和原坐标在主成分下的方向

主成分个数的确定：

• 贡献率：第i个主成分的方差在全部方差中所占比重，反映第i个主成分所提取的总信息的份额。
• 累计贡献率：前k个主成分在全部方差中所占比重
• 主成分个数的确定：累计贡献率>0.85

示例  

> library(stats)
> test <- iris[,1:4]
> data.pr <- princomp(test,cor = TRUE)
> summary(data.pr,loadings = TRUE)
Importance of components:
                          Comp.1    Comp.2     Comp.3      Comp.4
Standard deviation     1.7083611 0.9560494 0.38308860 0.143926497       #Standard deviation 标准差   其平方为方差=特征值
Proportion of Variance 0.7296245 0.2285076 0.03668922 0.005178709       #Proportion of Variance  方差贡献率
Cumulative Proportion  0.7296245 0.9581321 0.99482129 1.000000000   #Cumulative Proportion  方差累计贡献率 由结果显示 前两个主成分的累计贡献率已经达到96% 可以舍去另外两个主成分 达到降维的目的

Loadings:
             Comp.1 Comp.2 Comp.3 Comp.4
Sepal.Length  0.521 -0.377  0.720  0.261
Sepal.Width  -0.269 -0.923 -0.244 -0.124
Petal.Length  0.580        -0.142 -0.801
Petal.Width   0.565        -0.634  0.524

从summary()里我们可以看到，主成分分析法为我们生成了四个新的变量，第一个变量可以解释原数据73%的方差，第二个变量则可以解释元数据23%的方差。显然，这两个数据加起来已经可以解释原数据96%的信息了，所以我们可以用这两个新的变量代替原来四个初始变量。

 主成本碎石图： screeplot(data.pr,type = "lines")

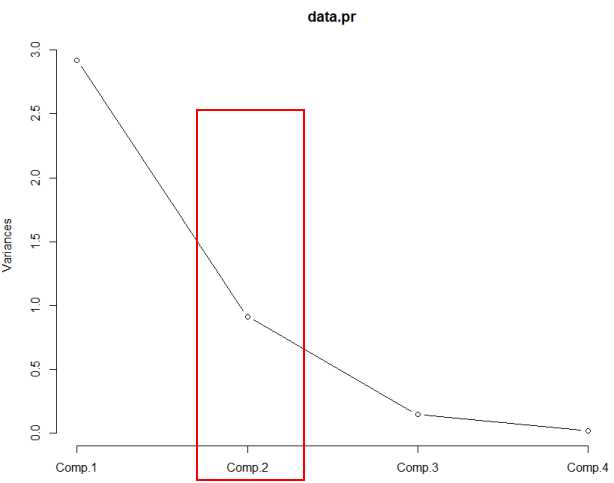
由碎石图可以看出 第二个主成分之后 图线变化趋于平稳 因此可以选择前两个主成分做分析

根据计算步骤对应的第5、6步，计算出降维后的数据集 

> newfeature<-as.matrix(test)%*%as.matrix(data.pr$loadings[,1:2])
> head(newfeature)
       Comp.1    Comp.2
[1,] 2.640270 -5.204041
[2,] 2.670730 -4.666910
[3,] 2.454606 -4.773636
[4,] 2.545517 -4.648463
[5,] 2.561228 -5.258629
[6,] 2.975946 -5.707321

疑问：通过predict 预测主成本的值 与 降维后新的数据集是什么关系？

> newfeature<-as.matrix(test)%*%as.matrix(data.pr$loadings[,1:2])
> head(newfeature)
       Comp.1    Comp.2
[1,] 2.640270 -5.204041
[2,] 2.670730 -4.666910
[3,] 2.454606 -4.773636
[4,] 2.545517 -4.648463
[5,] 2.561228 -5.258629
[6,] 2.975946 -5.707321
> 
> p <- predict(data.pr)
> head(p)
        Comp.1     Comp.2      Comp.3      Comp.4
[1,] -2.264703 -0.4800266  0.12770602  0.02416820
[2,] -2.080961  0.6741336  0.23460885  0.10300677
[3,] -2.364229  0.3419080 -0.04420148  0.02837705
[4,] -2.299384  0.5973945 -0.09129011 -0.06595556
[5,] -2.389842 -0.6468354 -0.01573820 -0.03592281
[6,] -2.075631 -1.4891775 -0.02696829  0.00660818

stats::prcomp

   prcomp（）和princomp( )，前者采用观测阵的奇异值分解方法，后者采用相关系数阵的特征值分解方法。输出结果上，包括特征值，载荷，主成分得分等，结果基本相似。区别如下：

• observation： 指 所有观察到的记录数，也就是数据集里面的行数
• variable：是指因素的个数
• R mode： 是指基于variable的分析 ，意思就是说在所有的observation里面，来研究variable之间的关系，哪些是主要的？是典型的？
• Q mode： 是指基于observation的分析，意思就是说在所有的variable里面，来研究observation之间的关系，哪两条记录相似？

  Usage： prcomp(formula, data = NULL, subset, na.action, ...)

• formula：在公式方法中设定的没有因变量的公式，用来指明数据分析用到的数据框汇中的列，
• data：包含在formula中指定的数据的数据框对象
• subset：向量对象，用来指定分析时用到的观测值，其为可选参数
• na.action:指定处理缺失值的函数

  prcomp(x, retx = TRUE, center = TRUE, scale = FALSE,tol = NULL, ...)

• x：在默认的方法下，指定用来分析的数值型或者复数矩阵
• retx：逻辑变量，指定是否返回旋转变量
• center：逻辑变量，指定是否将变量中心化
• scale：逻辑变量，指定是否将变量标准化
• tol：数值型变量，用来指定精度，小于该数值的值将被忽略

 示例 ：

> prC <- prcomp(iris[,1:4])
> summary(prC)
Importance of components:
                          PC1     PC2    PC3     PC4
Standard deviation     2.0563 0.49262 0.2797 0.15439
Proportion of Variance 0.9246 0.05307 0.0171 0.00521
Cumulative Proportion  0.9246 0.97769 0.9948 1.00000
> prC$rotation
                     PC1         PC2         PC3        PC4
Sepal.Length  0.36138659 -0.65658877  0.58202985  0.3154872
Sepal.Width  -0.08452251 -0.73016143 -0.59791083 -0.3197231
Petal.Length  0.85667061  0.17337266 -0.07623608 -0.4798390
Petal.Width   0.35828920  0.07548102 -0.54583143  0.7536574
> 
> newfeature<-as.matrix(iris[,1:4])%*%as.matrix(prC$rotation[,1:2])
> head(newfeature)
          PC1       PC2
[1,] 2.818240 -5.646350
[2,] 2.788223 -5.149951
[3,] 2.613375 -5.182003
[4,] 2.757022 -5.008654
[5,] 2.773649 -5.653707
[6,] 3.221505 -6.068283

其它R包

•  SciViews包的pcomp（）

• psych包的principal( )
• labdsv包pca( )
• ade4包 pca( )
• FactoMineR包 PCA（）
• rrcov 包Pca（）
• seacarb包pCa（）

ML: 降维算法-PCA

标签：根据   cti   matrix   standard   卡尔   数据分析   很多   协方差矩阵   日期   

原文地址：http://www.cnblogs.com/tgzhu/p/7363913.html