标签:个人 均值 初始化 讲解 dbscan src bsp 网格 soft
前言
以下内容是个人学习之后的感悟,转载请注明出处~
简介
在之前发表的线性回归、逻辑回归、神经网络、SVM支持向量机等算法都是监督学习算法,需要样本进行训练,且
样本的类别是知道的。接下来要介绍的是非监督学习算法,其样本的类别是未知的。非监督学习算法中,比较有代表性
的就是聚类算法。而聚类算法中,又有
以上只是部分算法,在这里就不一一列举了,本文讲解的是K-means算法。
K-means原理
K-means算法原理十分简单,实行起来总共分为以下几个步骤:
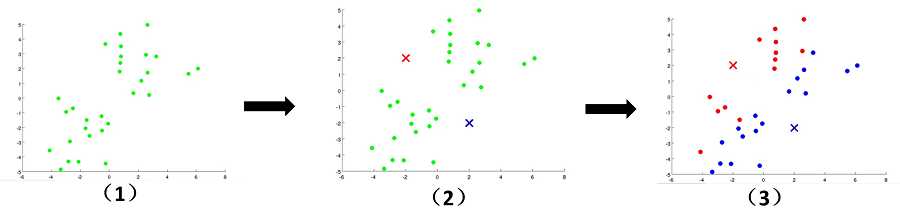
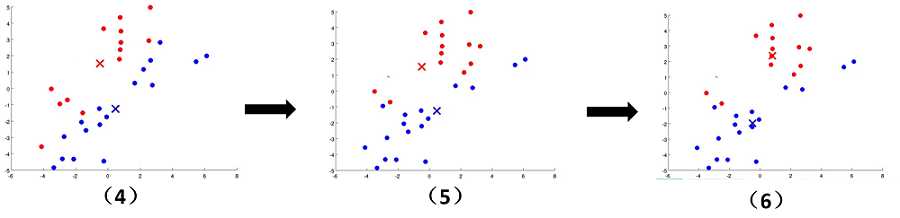
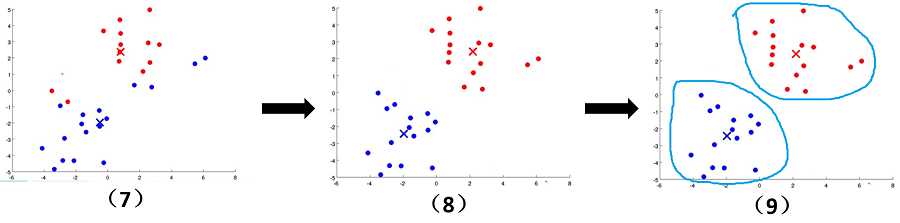
文字往往没有这么直观,接下来看下面的图片,我们可以清晰地看到聚类中心的变化,簇的变化。随着上面步骤的结束,
K-means算法到达了我们想要的效果。
K-means参数优化
1、代价函数
这代价函数很好理解,最小化此代价函数,无非是最小化每个样本到所属类簇中心的距离,此时的分类效果很好。
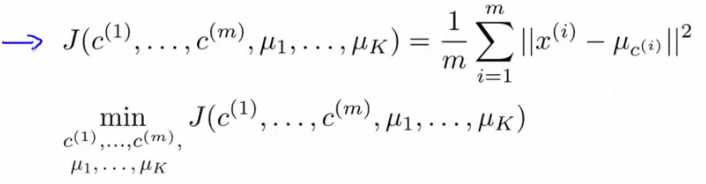
2、选择初始化聚类中心
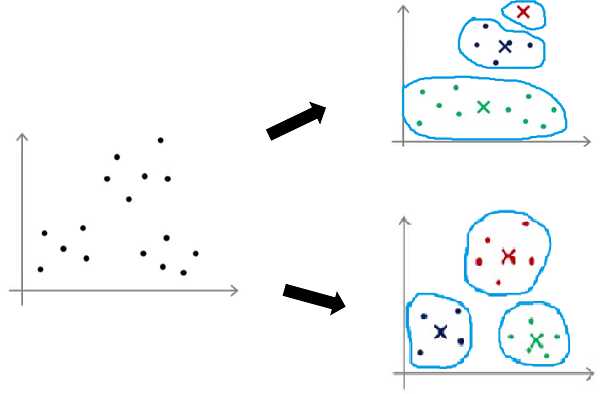
如果采用随机初始化,很可能导致结果的不理想,下图是两个不同初始化聚类中心的分类效果,明显下面这个分类效果好
多了,所以一次随机初始化,并不能给我们带来理想的效果。
那我们该怎么选择初始聚类中心呢?其实只需多次随机初始化,并运行算法,计算其代价函数,选择代价函数值小的初
始化聚类中心。

3、选择聚类的数目
如何选择聚类的数目?说实话,没有特别标准的答案。一般来说,手动选取比较多,或者采用“肘部法则”(Elbow method),
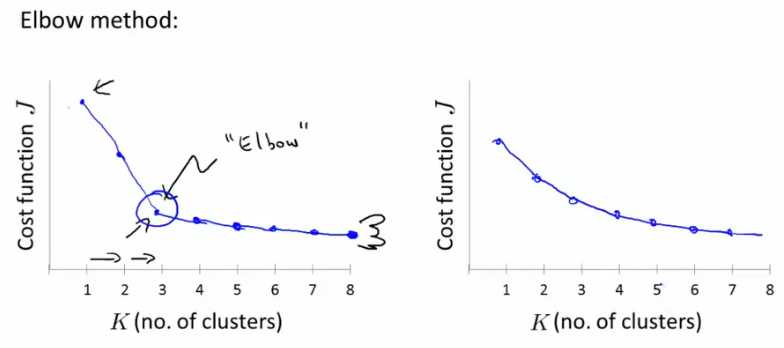
此法则是计算不同聚类数目下的代价函数,画出曲线,选择这个转折点(像肘部)的K值作为聚类数目,如下面左图所示。但是,现实
中的情况往往是下面右图所示,很难找到“肘部”。
注意:其实很多时候,你要分类的目标会给你相应的信息,需要分几类,此时你完全可以按照目标的要求来。
以上是全部内容,如果有什么地方不对,请在下面留言,谢谢~
标签:个人 均值 初始化 讲解 dbscan src bsp 网格 soft
原文地址:http://www.cnblogs.com/steed/p/7452728.html