标签:深度 cto img 过程 static space logs i++ 回溯
实际上回溯法有暴力破解的意思在里面,解决一个问题,一路走到底,路无法通,返回寻找另 一条路。
回溯法可以解决很多的问题,如:N皇后问题和迷宫问题。
一.概念
回溯算法实际类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现不满足条件的时候,就回溯返回,尝试别的路径。
百度解释:回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
二.基本思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)。
若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
而若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
三.n皇后问题
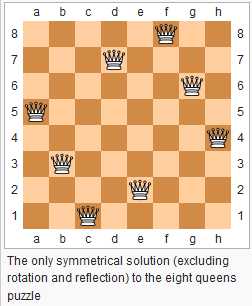
////N皇后是典型DPS问题,这里是用递归实现的,要想输出必须要存储上级运算结果。 #include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<string> #include<cctype> #include<cmath> #include<map> #include<set> #include<vector> #include<queue> #include<stack> #include<ctime> #include<algorithm> #include<climits> using namespace std; const int N=101; static int disp[16]; int C[N]; int tot; int n; void search(int cur) { if(cur==n){ for( int i = 0; i<n; i++ ) printf( "%d " , disp[i] ); printf("\n"); tot++; } else for(int i=0;i<n;i++) { int ok=1; C[cur]=i;//尝试把cur行的皇后放在第i列 for(int j=0;j<cur;j++)//检查是否和前面的皇后冲突 if(C[cur]==C[j]||cur-C[cur]==j-C[j]||cur+C[cur]==j+C[j]) { ok=0;break; } if(ok) { disp[cur]=i;//当前行的皇后在第几列 search(cur+1); } } } int main() { while(cin>>n) { tot=0; search(0); cout<<tot<<"种方法"<<endl; } return 0; }
#include <algorithm> #include <iostream> #include <cstdlib> #include <cstring> #include <cstdio> #include <cmath> using namespace std; int c[150],vis[3][150],tot,n=8,sum_max; int mapn[9][9]; void search(int cur) { if(cur==n)//递归边界,只要走到了这里,所有皇后必然不冲突 { if(sum_max<tot) sum_max = tot; } else for(int i=0;i<n;i++) { if(!vis[0][i]&&!vis[1][cur+i]&&!vis[2][cur-i+n])//利用二维数组直接判断 {//0为竖行,1为副对角线,2为主对角线 c[cur] = i;//保存下每行皇后的位置 tot += mapn[cur][i]; vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 1; search(cur+1); vis[0][i] = vis[1][cur+i] = vis[2][cur-i+n] = 0;//记得改回来 tot -= mapn[cur][i]; } } } int main() { int T; cin >> T; while(T--) { sum_max = 0,tot = 0; memset(vis,0,sizeof(vis)); for(int i=0;i<8;i++) for(int j=0;j<8;j++) { cin >> mapn[i][j]; } search(0); printf("%5d\n",sum_max); } return 0; }
算法入门经典-第七章 例题7-4-1 拓展 n皇后问题 回溯法
标签:深度 cto img 过程 static space logs i++ 回溯
原文地址:http://www.cnblogs.com/is-Tina/p/7502843.html