标签:后缀数组 turn images algorithm 有一个 printf mat 题意 bsp
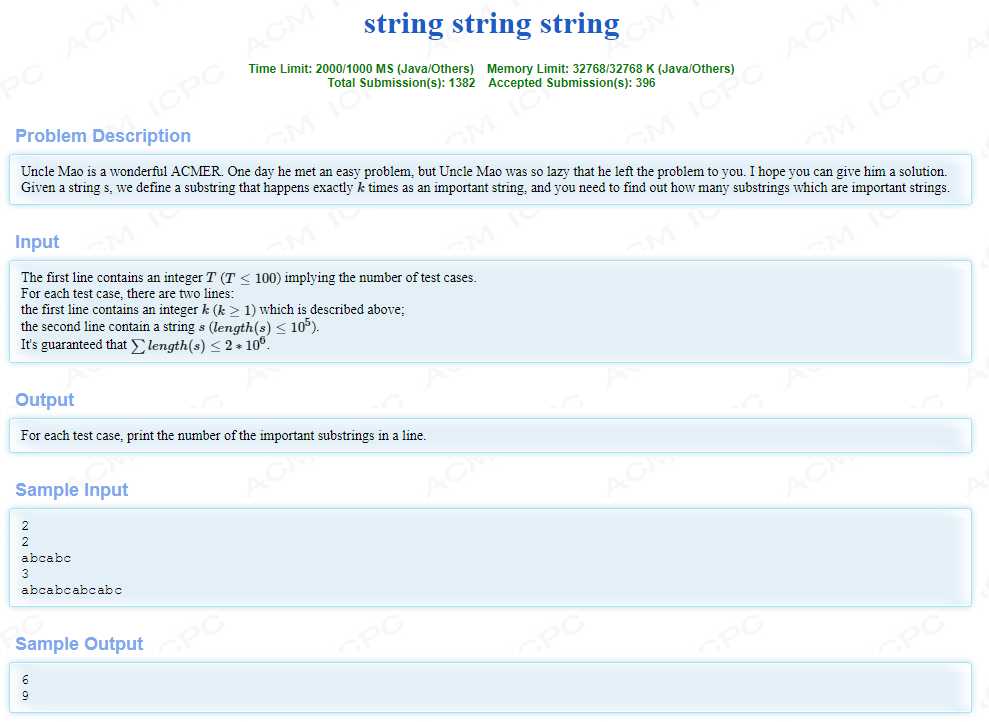
题意:求出现恰好 k次的子串(可以重叠)的个数;
分析:
刚开始想到了是后缀数组,但是有什么性质,具体怎么做的没有想到。回到主题来:
连续 k 次,说明这 k 个后缀排序后在一起,每次枚举 长度的为 k 的区间,用RMQ算出最长公共前缀长度,这里就有 len 个子串是 符合满足 k 次的,但是又有可能过短而不止出现了 k次,那么有多少呢?
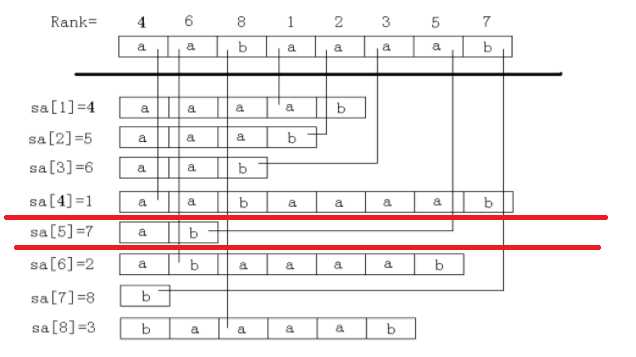
那么就是 a 不属于,len - height[j+1],前面也一样。也就是每次只算他独有的子串,但是你可能问 len > k 的时候,可以从新组成一组子串!
没关系,他会在下一个 k 的区间内出现~~~
到这里,离成功就只差一步了, k = 1 的时候,什么意思? 独一无二的子串个数,这时区间内只有一个后缀,那么就有 len - sa[i] 个后缀是至少有 1 次的,再次去掉 那些>1 次的子串(height[i] ,height[j+1])
#include <cstdio> #include <cmath> #include <cstring> #include <algorithm> using namespace std; const int maxn = 2000000+5; int wa[maxn],wb[maxn],wv[maxn],ws[maxn]; int sa[maxn]; int r[maxn]; int cmp(int *r,int a,int b,int l) { return r[a]==r[b]&&r[a+l]==r[b+l]; } void da(int *r,int *sa,int n,int m) { int i,j,p,*x=wa,*y=wb,*t; for(i=0; i<m; i++) ws[i]=0; for(i=0; i<n; i++) ws[x[i]=r[i]]++; for(i=1; i<m; i++) ws[i]+=ws[i-1]; for(i=n-1; i>=0; i--) sa[--ws[x[i]]]=i; for(j=1,p=1; p<n; j*=2,m=p) { for(p=0,i=n-j; i<n; i++) y[p++]=i; for(i=0; i<n; i++) if(sa[i]>=j) y[p++]=sa[i]-j; for(i=0; i<n; i++) wv[i]=x[y[i]]; for(i=0; i<m; i++) ws[i]=0; for(i=0; i<n; i++) ws[wv[i]]++; for(i=1; i<m; i++) ws[i]+=ws[i-1]; for(i=n-1; i>=0; i--) sa[--ws[wv[i]]]=y[i]; for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1; i<n; i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; } return; } int ranks[maxn],height[maxn]; void calheight(int *r,int *sa,int n) { int i,j,k=0; for(i=1; i<=n; i++) ranks[sa[i]]=i; for(i=0; i<n; height[ranks[i++]]=k) for(k?k--:0,j=sa[ranks[i]-1]; r[i+k]==r[j+k]; k++); return; } char str[maxn]; int f[maxn][20]; void init(int len) { for(int i = 1; i <= len; i++) f[i][0] = height[i]; for(int s = 1; (1<<s)<=len; s++) { int tmp = (1<<s); for(int i = 1; i+tmp-1<=len; i++) { f[i][s] = min(f[i][s-1],f[i+tmp/2][s-1]); } } } int cal(int l,int r) { int len = log2(r-l+1); int ans = min(f[l][len],f[r-(1<<len)+1][len]); return ans; } int main() { int t; scanf("%d",&t); while(t--) { int k; scanf("%d%s",&k,str); int len = strlen(str); for(int i = 0; i < len; i++) r[i] = str[i] - ‘a‘ + 1; r[len] = 0; da(r,sa,len+1,130); calheight(r,sa,len); init(len); int ans = 0; for(int i = 1; i+k-1<=len; i++) { int j = i+k-1; int tmp = height[i]; if(j+1<=len) tmp = max(tmp,height[j+1]); int x; if(k!=1) { x = cal(i+1,j); } else x = len - sa[i]; ans +=max(0,x-tmp); } printf("%d\n",ans); } return 0; }
标签:后缀数组 turn images algorithm 有一个 printf mat 题意 bsp
原文地址:http://www.cnblogs.com/TreeDream/p/7522480.html