标签:image ima 基本 min 拉格朗日乘子 数据线 基础 lin ctr
支持向量机
支持向量机(support vector machines,SVMs)是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;支持向量机还包括核技巧,这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的问题。
支持向量机学习方法包含构建由简至繁的模型:线性可分支持向量机(linear support vector machine in linearly separable case)、线性支持向量机(linear support vector machine)及非线性支持向量机(non-linear support vector machine)。简单模型是复杂模型的基础,也是复杂模型的特殊情况。当训练数据线性可分时,通过硬间隔最大化(hard margin maximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization),也学习一个线性的分类器,即线性支持向量机,又称为软间隔支持向量机;当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机。通过使用核函数可以学习非线性支持向量机,等价于隐式地在高维的特征空间中学习线性支持向量机。核方法(kernel method)是比支持向量机更为一般的机器学习方法。
线性可分支持向量机与硬间隔最大化
支持向量机的学习是在特征空间进行的。假设给定一个特征空间上的训练数据集,其中,
,
为第i个特征向量,也称为实例,
为
的类标记,当
=+1时,称
为正例;当
=-1时,称
为负例,
称为样本点。再假设训练数据集是线性可分的。
学习的目标实在特征空间中寻找一个分离超平面,能将实例分到不同的类。分离超平面对应于方程,它由法向量
和截距
决定,可用
来表示。
一般地,当训练数据集线性可分时,存在无穷个分离超平面可将两类数据正确分开。线性可分支持向量机利用间隔最大化求最优分离超平面,这时,解是唯一的。
定义(线性可分支持向量机)给定线性可分训练数据集,通过间隔最大化或等价地求解相应的凸二次规划问题学习得到的分离超平面为:
以及相应的分类决策函数称为线性可分支持向量机。
算法(线性可分支持向量机学习算法——最大间隔法)
输入:线性可分训练数据集,其中,
,
,
;
输出:最大间隔分离超平面和分类决策函数。
(1)构造并求解约束最优化问题:
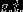
,
求得最优解,
。
(2)由此得到分离超平面:
分类决策函数
在线性可分情况下,训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量(support vector)。支持向量是使约束条件等号成立的点,即
对的正例点,支持向量在超平面
上,
对的负例点,支持向量在超平面
上。
和
称为间隔边界。
在决定分离超平面时只有支持向量起作用,而其他实例点并不起作用。
那么,上述算法中的和
是怎么得到的呢?
想要求解线性可分支持向量机的最优化问题,将它作为原始最优化问题,应用拉格朗日对偶性,通过求解对偶问题(dual problem)得到原始问题(primal problem)的最优解,这就是线性可分支持向量机的对偶算法(dual problem)。这样做的有点,一是对偶问题往往更容易求解;二是自然引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数(Lagrange function)。为此,对每一个不等式约束引进拉格朗日乘子(Lagrange multiplier),
,定义拉格朗日函数:
其中,为拉格朗日乘子向量。
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
所以,为了得到对偶问题的解,需要先求对w,b的极小,再求对
的极大。
(1)求
将拉格朗日函数分别对w,b求偏导数并令其等于0。
得
将上述两式带入拉格朗日函数,即得
即
(2)求对
的极大,即是对偶问题
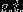
,i=1,2,...,N
将上述目标函数由极大转换成极小,就得到下面与之等价的对偶最优化问题:
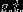
,i=1,2,...,N
设是对偶最优化问题的解,则存在下标j,使得
,并可按下式求得原始最优化问题的解
,
:
机器学习之支持向量机(Support Vector Machine)(更新中...)
标签:image ima 基本 min 拉格朗日乘子 数据线 基础 lin ctr
原文地址:http://www.cnblogs.com/Peyton-Li/p/7536927.html