标签:ict char 自己 比较 image class 数据 还需 nta
今天遇到了一道字典树的题,这是我第一次使用字典树来解决问题,所以我觉得还是有必要记录下来。
题意:
设计一个包含下面两个操作的数据结构:addWord(word), search(word) addWord(word)会在数据结构中添加一个单词。而search(word)则支持普 通的单词查询或是只包含.和a-z的简易正则表达式的查询。 一个 . 可以代表一个任何的字母。
样例:
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") // return false
search("bad") // return true
search(".ad") // return true
search("b..") // return true
注意事项:
你可以假设所有的单词都只包含小写字母 a-z。
1.字典树
字典树又称为单词查找树,是一个树形结构,是哈希树的变种。它的优点:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
同时,它还有3个性质:
A.根节点不包含字符,除根节点外每一个节点都只包含一个字符;
B.从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串;
C.每个节点的所有子节点包含的字符都不相同。
如图所示:
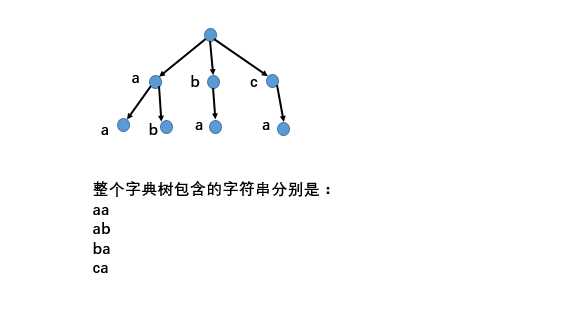
2.构建字典树
从上面的介绍,我们能简单的知道,字典树每一个节点里面包含了两个东西,一个是value,也就是数据,第二个是孩子,这里是孩子们,因为一个节点可能有多个孩子,不只是有1个或者2个孩子节点。
但是这里我们还需要一个flag来判断当前这个节点是否是最终节点,也就是判断这个节点是否还有孩子。为什么要这么做呢?比如,在字典树中有一个字符串是:abcd,我们想在字典树中查找abc,我们发现abcd这个路径符合要求,因为每个字符都匹配了的,但是这样判断是错误的,所以我们得判断每个节点是否是最终节点。
(1).节点的封装
private class TreeNode { //节点的值 public char value; //节点的孩子们 public TreeNode child[] = null; //是否是最终节点 public boolean isEnd = false; public TreeNode(char value) { this.value = value; child = new TreeNode[26]; } }
(2).向字典树中添加字符
public void addWord(String word) { TreeNode node = root; for (int i = 0; i < word.length(); i++) { char c = word.charAt(i); if (node.child[c - ‘a‘] == null) { node.child[c - ‘a‘] = new TreeNode(c); } node = node.child[c - ‘a‘]; } //该节点最为最终节点 node.isEnd = true; }
3.在字典树中查找单词
在普通的查找中(查找的单词不含通配符,全部是字符),自己循环查找就是,但是在这里比较特殊,查找的单词可能还有通配符,那么就不能使用普通的查找了,这里我使用的回溯法来查找的,使用回溯法将符合要求的字符串添加到一个List集合中,然后在判断一下,在这个List集合是否有我们想要的字符串。
1 public class WordDictionary { 2 3 private TreeNode root = null; 4 private List<String> list = null; 5 6 public WordDictionary() { 7 root = new TreeNode(‘ ‘); 8 list = new ArrayList<>(); 9 } 10 11 private class TreeNode { 12 //节点的值 13 public char value; 14 //节点的孩子们 15 public TreeNode child[] = null; 16 //是否是最终节点 17 public boolean isEnd = false; 18 19 public TreeNode(char value) { 20 this.value = value; 21 child = new TreeNode[26]; 22 } 23 } 24 25 public void addWord(String word) { 26 TreeNode node = root; 27 for (int i = 0; i < word.length(); i++) { 28 char c = word.charAt(i); 29 if (node.child[c - ‘a‘] == null) { 30 node.child[c - ‘a‘] = new TreeNode(c); 31 } 32 node = node.child[c - ‘a‘]; 33 } 34 //该节点最为最终节点 35 node.isEnd = true; 36 } 37 38 public boolean search(String word) { 39 TreeNode node = root; 40 list.clear(); 41 char cs[] = new char[word.length()]; 42 Arrays.fill(cs, ‘ ‘); 43 backTrack(word, 0, node, cs); 44 //判断是否含有word字符串 45 return list.contains(word); 46 } 47 48 private void backTrack(String word, int i, TreeNode node, char cs[]) { 49 //当i < word.length() 继续搜索下去 50 if (i < word.length()) { 51 char c = word.charAt(i); 52 if (c != ‘.‘) { 53 if (node.child[c - ‘a‘] != null) { 54 cs[i] = c; 55 backTrack(word, i + 1, node.child[c - ‘a‘], cs); 56 } 57 } else { 58 for (int j = 0; j < 26; j++) { 59 if (node.child[j] != null) { 60 cs[i] = ‘.‘; 61 backTrack(word, i + 1, node.child[j], cs); 62 } 63 } 64 } 65 } else { 66 //node不为最终节点,所以不符合要求 67 if(!node.isEnd){ 68 return; 69 } 70 StringBuilder stringBuilder = new StringBuilder(); 71 for (int j = 0; j < word.length(); j++) { 72 stringBuilder.append(cs[j]); 73 } 74 list.add(stringBuilder.toString()); 75 } 76 77 } 78 }
标签:ict char 自己 比较 image class 数据 还需 nta
原文地址:http://www.cnblogs.com/Stay-Hungry-Stay-Foolish/p/7537789.html