标签:元素 数据结构 不同 意义 div 它的 end 差分 else
树状数组是一种修改查找复杂度都是logN的实用的数据结构,大家应该都会,下面放一张熟的不能再熟的图装装样子
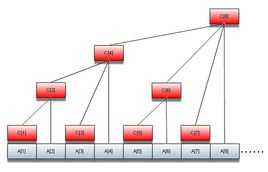
树状数组最基本的操作:单点修改,前缀查询。原理都懂就不赘述了,贴个代码。
void add(int pos,int x) { for(;pos<=N;pos+=lowbit(pos)) c[pos]+=x; } int query(int pos) { int sum=0; for(;pos;pos-=lowbit(pos)) sum+=c[pos]; return sum; }
有一种进阶操作,区间修改,单点查询 。
这就要用到差分——让一个位置的前缀和等于它的值。所以查单点就就是查前缀和。
那如何修改区间呢, 举个例子 比如我们让 区间4 5 7加上3
原数组 1 4 5 7 10 -> 1 7 8 10 10
差分数组 1 3 1 2 3 -> 1 6 1 2 0
显而易见,整个区间加上一个数, 区间内部元素的差是不变的。
在差分数组中,只有这个区间两头的数字改变了 (挺好理解的吧)
于是 , 就可以通过单点修改区间的两端来进行区间修改了。
代码的话 基本操作和上面是一样的,只是意义不同了 , 唯一不一样的是读入的时候存的是差分数组
for(int i=1;i<=N;i++) { cin>>a[i]; add(i,a[i]-a[i-1]); }
现在你们可能有一个大胆的想法 : 怎么实现区间修改区间查询
下面就是奇技淫巧时间。 (标题已上线)
还是要用差分数组, 下面我们简单推个式子。
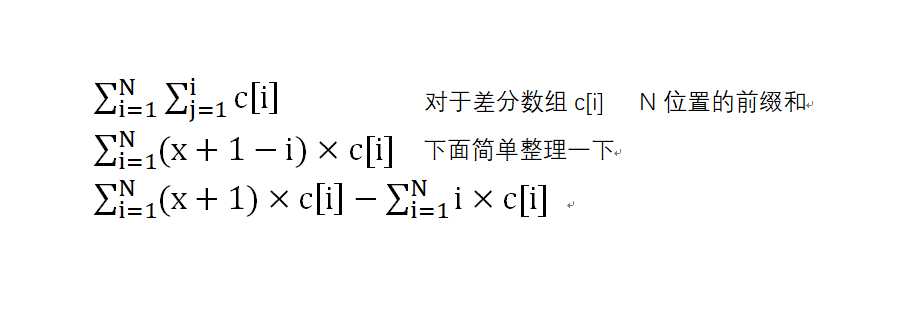
所以我们就可以开两个数状数组, 一个里面放c[i],一个里面放 i×c[i],就能实现区间查询了
除了每次修改改的是两个数组, 其他操作都一样
下面是代码
#include<bits/stdc++.h> #define ull unsigned long long #define lowbit(a) (a&-a) #define MAXN 200005 using namespace std; int N,M,a[MAXN]; ull c1[MAXN],c2[MAXN]; void add(int pos,ull x) { for(int i=pos;i<=N;i+=lowbit(i)) c1[i]+=x,c2[i]+=x*pos; } ull sum(int pos) //[1,pos]区间和 { ull s=0; for(int i=pos;i;i-=lowbit(i)) s+=c1[i]*(pos+1)-c2[i]; return s; } int main() { ios::sync_with_stdio(false); cin>>N; for(int i=1;i<=N;i++) { cin>>a[i]; add(i,a[i]-a[i-1]); } cin>>M; while(M--) { int P,X,Y; ull Z; cin>>P; if(P==1) { cin>>X>>Y>>Z; add(Y+1,-Z); add(X,Z); } else if(P==2) { cin>>X>>Y; cout<<sum(Y)-sum(X-1)<<endl; } } return 0; }
可以到 http://codevs.cn/problem/1082/ 交一下练练手
好了就说这么多了。
其实, 我想去学线段树了。。。
标签:元素 数据结构 不同 意义 div 它的 end 差分 else
原文地址:http://www.cnblogs.com/Elfish/p/7544623.html