三种参数估计算法

标签：src   贝叶斯公式   和我   auto   通过   原则   定义   例子   tail   

作为一名机器学习中的小白，参数估计方法的学习必不可少，本着边学习边记录的原则，并参考一些其他博客或资源，作为打开我开始机器学习的第一扇门。

先说说统计学中的两大派别：频率派和贝叶斯学派。

频率派认为：参数是客观存在的，不会改变，虽然未知，但却是固定值。——似然函数

贝叶斯学派认为：参数是随机值，虽没有观察到，但和随机数一样，也有自己的分布。——后验概率，贝叶斯估计

• 在学习参数估计方法前，我觉得还是有必要复习（其实是预习）一下概率中几种重要的分布，因为在后面的参数估计方法中有用到过。

1. 伯努利分布：伯努利试验：一次试验成功：p 一次实验失败：（1-p）
2. 二项分布：n次伯努利实验：X~（n,p）
3. 多项式分布：二项分布的推广，这里不重点介绍，需要复习的同学可以看下面的链接。
4. Beta分布：这是本文的重点。举例：当我们投掷硬币时，投掷10次，如果投掷结果全部是正面向上（当然这种概率较小，但也是可能出现的），那么你可能会错误的估计投掷硬币正面向上的结果是100%（这就是极大似然参数估计的结果）。显然按照“常识”我们都知道，投掷硬币正面向上的概率是50%（这里的常识我们可以看成先验知识）。说了这么多终于可以引出我们的beta分布了，beta分布就是利用这些先验知识，将这些先验信息用分布表示出来，增加先验知识来参数估计（最大后验概率估计-MAP）,消除最大似然估计可能导致的误差。至于beta分布是什么，这里链接一篇我觉得解释的不错的知乎，供大家参考。beta分布：https://www.zhihu.com/question/30269898
5. Dirichlet分布：与多项分布是共轭分布，即：与多项分布具有相同的分布形式。

• 预备知识二：独立同分布（参数估计有一个很重要的假设条件就是独立同分布采样）

1. 独立：P（AB）=P（A）×P（B）——互相之间发生互不影响的两个时间相互独立
2. 同分布：分布相同的随机变量（例如都服从0-1分布）
3. 举例：从一个装有红，黄两种颜色小球的盒子里多次有放回的取出一个小球，每次取出小球的事件互不影响，并且小球总数不变（即分布相同）

对于参数估计算法来说，一般都会引用“模型已定，参数未知”来很好的解释，即已知变量的概率分布，但其中的参数未知。本文介绍三种参数估计方法：MLE，MAP和贝叶斯估计。首先再次引入贝叶斯公式（这个公式真的是很强大）：

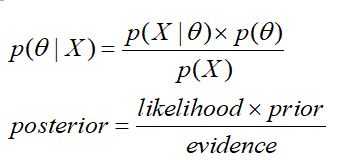
极大似然估计：只考虑likelihood（似然），可能这就是为什么叫似然估计（不知道这样理解对不对）

最大后验估计：同时考虑likelihood×prior来等价于后验概率

贝叶斯估计：整体考虑等式右边 

• 极大似然估计（Maximum Likelihood Estimate，MLE）：

极大似然估计，即最大化似然函数来进行参数估计，这里的似然函数的自变量是参数θ，而不是随机变量X。

首先介绍什么是似然函数。先用一个简单的例子：投掷两次硬币，首先给出结果：两次投掷正面向上，反问：在投掷一次硬币正面向上的概率为多少时，出现这样的结果的概率最大（即：似然最大）。当我们取p（H）正面向上的概率为0.6与0.5时，我们可以得出:p(0.6|HH)=0.6×0.6=0.36 > p(0.5|HH)=0.25,所以我们认为p(H)=0.6时，比p(H)=0.5投掷两次硬币出现正面向上的似然更大，其实最大时是p(H) = 1,但实际我们都知道p(H) = 0.5，这就是MLE可能出现的误差。

一般的概率密度（PDF）函数都是将随机变量自变量（因为参数已知），而似然函数就是在参数未知时，将自变量与参数调换一下位置即为似然函数：L（θ|X）=f(X|θ)。

首先给出MLE算法的一般步骤：

1. 写出似然函数
2. 写出似然函数的对数，并整理（后面解释为什么，其实是方便化简）
3. 求导
4. 求解似然函数

假设（x₁,x₂,...,x_n)为独立同分布采样，θ为参数模型，f为函数模型。

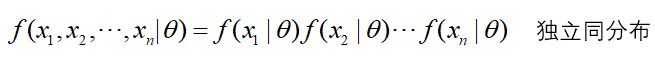其中x₁,x₂,...,x_n已知，θ未知。似然定义：

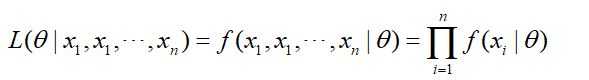两边取对数得到对数似然：

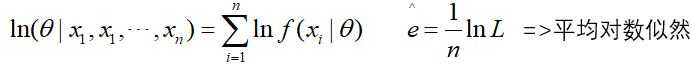一般直接求最大似然为平均对数的最大，即：

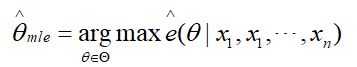注：最大似然估计只考虑某个模型产生某个给定的观察序列的概率，不考虑模型本身，这一点和贝叶斯估计不同。

 例题可以看看：http://blog.csdn.net/leo_xu06/article/details/51222215

下一篇：最大后验估计（MAP）

因为刚开始写博客，排版，公式安排的不是很好，特别是同时是通过mathtype写出来后截图上传的，博友们有更好的v办法望告知。

最后，请广大博友和我交流，我一般每天都在线，可以给大家及时回复。

 参考：

频率派和贝叶斯学派：http://blog.csdn.net/wzgbm/article/details/51721143

http://blog.csdn.net/whatwho_518/article/details/44855929

http://blog.csdn.net/wzgbm/article/details/51721143

三种参数估计算法

标签：src   贝叶斯公式   和我   auto   通过   原则   定义   例子   tail   

原文地址：http://www.cnblogs.com/gy-jhh-12138/p/7590392.html