标签:大于 return max lintcode display isp val integer 博客
今天在lintCode又做了一道关于非常规二分法的使用,觉得还是有必要记录下来。
题意:
给出一个数组A包含n个元素,表示n本书以及各自的页数。现在有个k个人复印 书籍,每个人只能复印连续一段编号的书,比如A[1],A[2]由第一个人复印,但 是不能A[1],A[3]由第一个人复印,求最少需要的时间复印所有书。
样例:
A = [3,2,4],k = 2
返回5,第一个人复印前两本书
这个题看上去感觉好难的样子,但是实际上,这个题非常的简单,就是一个二分法定区间的题。这种题在这之前,我也写了两篇关于非常规二分法使用的博客,相对来说,还是比较类似的。
1.解题思路
首先,我们假设只有一个人在复印书籍,那么使用的时间就是所有的书籍页数总和,我们假设是sum,如果有无数个人在复印书籍的话(实际上,我们看做是人数与书的数目相等,不是书的页数),那么使用的时间就是书籍的最大页数,我假设是max。因此,我们得出结论,k个人在复印书籍的话,使用的时间肯定在[max, sum]。
所以,我们可以在[max,sum]的区间上不断的二分,不断的缩小范围。其中方法是这样,我们计算出 mid = (start + end) /2(假设start = max, end = sum),然后计算出当最大页数是mid时,需要的人数,我们假设为count,如果count大于k的话,那么表示如果k个人复印mid页的话是不够的,如果需要增加每个人的复印页数(这个页数肯定在(mid, end]区间),因此start = mid;反之,表示每个人复印mid页印多了,k个人中有人可以不需要印,所以我们需要减少每个人的复印页数(这个页数肯定在[start,mid))。
但是这里有一个问题,就是这个二分的结束条件。之前的二分结束条件几乎都是 start < end,但是在这里却不一样了,因为如果结束还是那样的话,那么有可能出现死循环。例如:
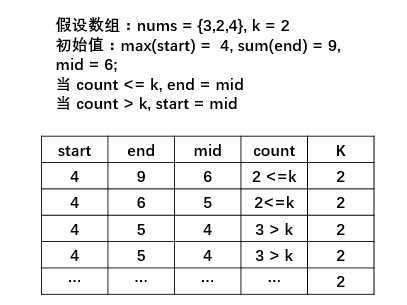
因此,在这里二分的结束条件不能设置为 start < mid, 应该是Start + 1 < mid。在最后的时候在计算一次,如果在start的情况下,count <= k,则返回start, 反之返回end。
2.代码
1 public static int copyBooks(int[] pages, int k) { 2 if (pages == null || pages.length == 0 || k == 0) { 3 return 0; 4 } 5 6 int max = Integer.MIN_VALUE; 7 int sum = 0; 8 //计算最大值和总和 9 for (int i : pages) { 10 if (i > max) { 11 max = i; 12 } 13 sum += i; 14 } 15 int start = max; 16 int end = sum; 17 //二分 18 while (start + 1 < end) { 19 int mid = (end - start) / 2 + start; 20 21 if (countCopier(pages, mid) > k) { 22 start = mid; 23 } else { 24 end = mid; 25 } 26 } 27 return start; 28 } 29 //计算在每个人复印limit页数的情况下,需要的人数 30 private static int countCopier(int pages[], int limit) { 31 int sum = pages[0]; 32 int copierCount = 1; 33 for (int i = 0; i < pages.length; i++) { 34 if(sum + pages[i] > limit) { 35 copierCount++; 36 sum = 0; 37 } 38 sum += pages[i]; 39 } 40 return copierCount; 41 }
标签:大于 return max lintcode display isp val integer 博客
原文地址:http://www.cnblogs.com/Stay-Hungry-Stay-Foolish/p/7593607.html