标签:nis .com 01背包问题 public 其他 最大化 理解 mat 分享
01背包是在M件物品取出若干件放在空间为W的背包里,每件物品的体积为W1,W2至Wn,与之相对应的价值为P1,P2至Pn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品,每种物品有且只有一个,并且有权值和体积两个属性。在01背包问题中,因为每种物品只有一个,对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中,则不需要处理。如果选择将其放入背包中,由于不清楚之前放入的物品占据了多大的空间,需要枚举将这个物品放入背包后可能占据背包空间的所有情况。
01背包的状态转换方程 f[i,j] = Max{ f[i-1,j-Wi]+Pi( j >= Wi ), f[i-1,j] }
f[i,j]表示在前i件物品中选择若干件放在承重为 j 的背包中,可以取得的最大价值。Pi表示第i件物品的价值。决策:为了背包中物品总价值最大化,第 i件物品应该放入背包中吗 ?我们只需要初始化第一行和第一列的数据,就可以根据状态转换方程进行计算所有的结果!我们只需要初始化第一行和第一列的数据,就可以根据状态转换方程进行计算所有的结果!我们只需要初始化第一行和第一列的数据,就可以根据状态转换方程进行计算所有的结果!
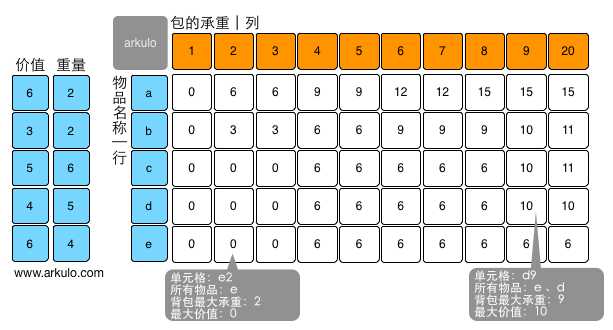
有了这张图和上面总结的公式,我们就可以很清晰的理解01背包算法了(倒序)!!!!!!!
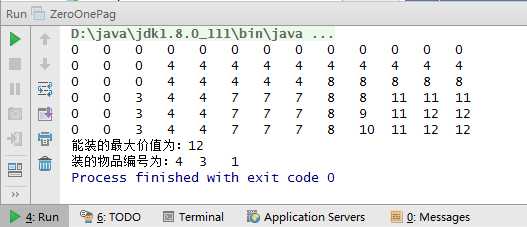
1 package com.niu.test; 2 3 /** 4 * Created by Administrator on 2017/10/3. 5 */ 6 public class ZeroOnePag { 7 8 /** 9 * w:代表物品的重量 10 * p:代表物品的价值 11 * pag:代表背包的大小 12 * @param args 13 */ 14 public static void main(String[] args) { 15 int[] w={3,5,2,6,4}; 16 int[] p={4,4,3,5,3}; 17 int pag=12; 18 table(pag,w,p); 19 20 } 21 22 static void table(int pag,int[] w,int[] p){ 23 int n=w.length; 24 //初始化f[0][1~pag]=0;f[1-n][o]=0;这样才能根据初始化根据公式推算其他的值! 25 int[][] f=new int[n+1][pag+1]; 26 //01背包算法f[i][j]=MAX{f[i-1][j-w[i]]+p[i](j>=w[i],f[i-1][j])} 27 //算法核心部分:根据公式进行推算!!!!! 28 for(int i=1;i<=n;i++){ 29 for(int j=1;j<=pag;j++){ 30 if(j>=w[i-1]){ 31 f[i][j]=Math.max(f[i-1][j-w[i-1]]+p[i-1],f[i-1][j]); 32 }else{ 33 f[i][j]=f[i-1][j]; 34 } 35 } 36 } 37 //输出表 38 for(int i=0;i<=n;i++){ 39 for(int j=0;j<=pag;j++){ 40 System.out.print(f[i][j]+"\t"); 41 } 42 System.out.print("\n"); 43 } 44 //输出最大值 45 System.out.println("能装的最大价值为:"+f[n][pag]); 46 //输出装的物品 47 System.out.print("装的物品编号为:"); 48 int x=pag; 49 for(int i=n;i>0;i--){ 50 if(f[i][x]>f[i-1][x]){ 51 System.out.print(i+"\t"); 52 x-=w[i-1]; 53 } 54 } 55 } 56 }
标签:nis .com 01背包问题 public 其他 最大化 理解 mat 分享
原文地址:http://www.cnblogs.com/yjqc/p/7623808.html