标签:改变 return height tle 转化 div 答案 alt accept
题目传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=3238
这道题从大概半年以前就开始啃了,不过当年因为一些细节没调出来,看了Sakits神犇的博客之后也没明白自己挂在哪里,于是就抄了个题解。然后现在突然想到填这个坑(其实是为了复习一下后缀数组模板),换了种思路才过了这道题……然而还是不知道当年那种写法为什么错……似乎是挂在判重?
解法(Accepted):
首先我们可以观察一下这个式子(见下),我们可以把它拆开,变成sigma(len(Ti)+len(Tj))-2*sigma(lcp(Ti,Tj))。其中前一项随便在纸上算一算就能得出为n*(n+1)*(n-1)/2。

后面的lcp总和,我们可以先用后缀数组将其转化为height数组的区间最小值之和。之前的写法是统计以height数组每个值作为最小值的区间有多少个,再来算答案,然而似乎可能会有重复计算,要加一坨判断。
但是我们可以改变一下统计方式,统计以每个数作为右端点的区间的最小值总和,然后把他们加起来。这里就要用到单调栈一个神奇的性质:把一个序列压进单调栈,这个序列的后缀最小/最大值一定会在单调栈中出现。于是可以转化为统计单调栈中每个数对最小值之和的贡献。计算方法见下图:
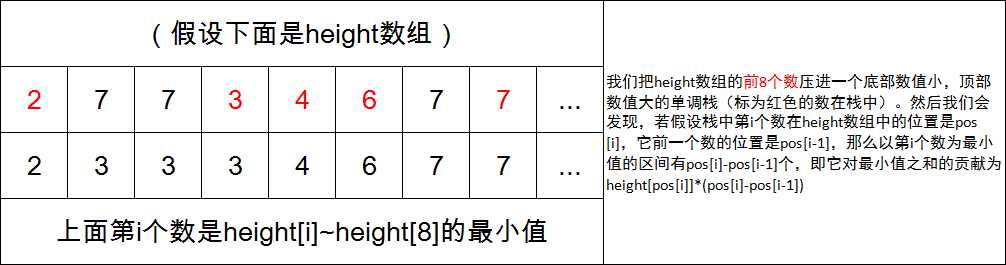
此外,因为栈中每个数的贡献从它被压进栈到弹出是不会变的,于是只要在压数和弹数时维护一下就能算出答案。
然后这道题就解决了^_^
代码:

#include<cstdio> #include<cmath> #include<cstring> #include<cstdlib> #include<ctime> #include<algorithm> #include<queue> #include<vector> #define ll long long #define maxn 500010 inline ll read() { ll tmp=0; char c=getchar(),f=1; while(c<‘0‘||‘9‘<c){if(c==‘-‘)f=-1; c=getchar();} while(‘0‘<=c&&c<=‘9‘){tmp=tmp*10+c-‘0‘; c=getchar();} return tmp*f; } char s[maxn]; ll sa[maxn],rk[maxn],tsa[maxn],trk[maxn],sum[maxn],h[maxn]; ll st[maxn]; ll n; void getsa() { int i,tot,cnt=256,len; for(i=1;i<=cnt;i++)sum[i]=0; for(i=0;i<n;i++)trk[i+1]=s[i]+1,++sum[trk[i+1]]; for(i=2;i<=cnt;i++)sum[i]+=sum[i-1]; for(i=n;i;i--)sa[sum[trk[i]]--]=i; cnt=1; rk[sa[1]]=1; for(i=2;i<=n;i++){ if(trk[sa[i]]!=trk[sa[i-1]])++cnt; rk[sa[i]]=cnt; } for(len=1;cnt<n;len<<=1){ for(i=1;i<=n;i++)trk[i]=rk[i]; for(i=1;i<=n;i++)sum[i]=0; tot=0; for(i=n-len+1;i<=n;i++)tsa[++tot]=i; for(i=1;i<=n;i++)if(sa[i]>len)tsa[++tot]=sa[i]-len; for(i=1;i<=n;i++)rk[i]=trk[tsa[i]],++sum[rk[i]]; for(i=2;i<=cnt;i++)sum[i]+=sum[i-1]; for(i=n;i;i--)sa[sum[rk[i]]--]=tsa[i]; cnt=1; rk[sa[1]]=1; for(i=2;i<=n;i++){ if(trk[sa[i]]!=trk[sa[i-1]]||trk[sa[i]+len]!=trk[sa[i-1]+len])++cnt; rk[sa[i]]=cnt; } } for(i=1;i<=n;i++){ if(rk[i]==1)continue; if(h[rk[i-1]]>0)h[rk[i]]=h[rk[i-1]]-1;else h[rk[i]]=0; while(s[i+h[rk[i]]-1]==s[sa[rk[i]-1]+h[rk[i]]-1])++h[rk[i]]; } } int main() { int i; scanf("%s",s); n=strlen(s); getsa(); ll top=0,ans=(n-1)*n*(n+1)/2,tot=0; st[0]=0; h[0]=-(1<<30); for(i=1;i<=n;i++){ while(h[st[top]]>=h[i]){ tot-=h[st[top]]*(st[top]-st[top-1]); --top; } tot+=h[i]*(i-st[top]); st[++top]=i; ans-=2*tot; } printf("%lld",ans); }
【bzoj3238】差异[AHOI2013](后缀数组+单调栈)
标签:改变 return height tle 转化 div 答案 alt accept
原文地址:http://www.cnblogs.com/quzhizhou/p/7627184.html