标签：社会主义 dwr ns3 atq baidu jid gdk sae lap
#PS：这是我好几年前写的Blog，一直没发出来，所以和我现在的风格不大一样，but现在修改了一部分，还不错~~#
今天，我们非常愉快地学习 如何去找“图”的“最小生成树”——Prim与Kruskal算法
什么叫做生成树？
简单的来说，我先给大家讲一个故事……
故事背景：
有一天，God•MTC告诉All around the world的老百姓，他要挑一个孩子将来当Cupid。怎么个挑法呢?他给所 有的孩子发了一粒花籽，看谁拿这粒花籽种出最美丽的Rose来。God•MTC还非常心血来潮地画了花的设计图：
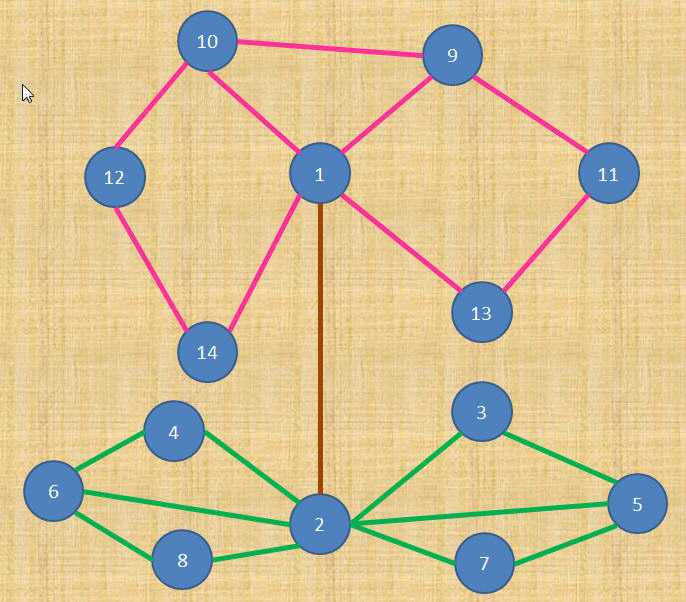很明显，God•MTC的小学美术肯定是数学老师教的，所以他在图上施了魔法，还要求孩子们种出来的Rose一定要像图上的一样“美丽”，不然就把他们统统扔进二次元 (qwq) ……然而，种子是炒熟了的，这显然是God•MTC的一场阴谋（哦天，暴君还没被推翻真是奇迹 !(À_Á)!）。
God•MTC还恐吓孩子们：“这颗种子是非常珍贵的！开出来的花都是金做的！” 导致孩子们不得不在通货膨胀的时代用昂贵的金子去做一朵假花（垄断资本主义的腐臭味儿……）。富家子女当然随随便便能拿到足够的金子；但是满腔热血、勤俭节约，践行社会主义核心价值观，自觉传承中华民族优秀传统文化的中华儿女，肯定是希望用最少的金子去做出Rose的样子来。God•MTC的手下大义凛然地分享了一个秘密：God•MTC有高度的近视，所以只要把设计图上花朵的端点连起来，God•MTC就看不出来的。//%% MTCheng all rights reserved %%//
生成树：
于是，为了保证连通图里每个顶点都能够被连接上，并且能够最节省花边数量的“设计图”，就叫做“生成树”。
（想一想，连接两个顶点最少需要一条花边，三个顶点最少需要两条花边，那么连接n个呢——当然是（n-1）条花边啦）我大天朝子民的想象力是极为丰富的：
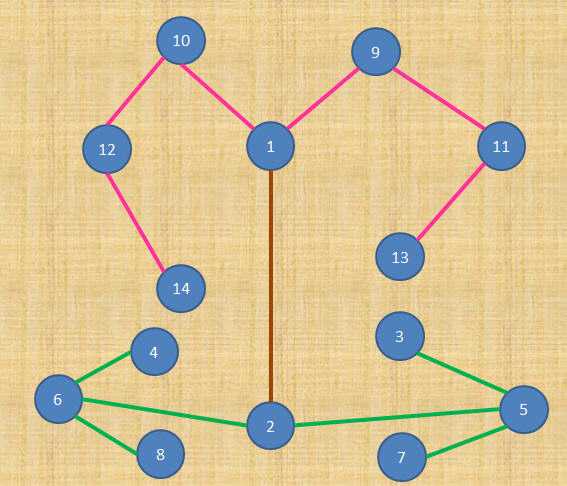
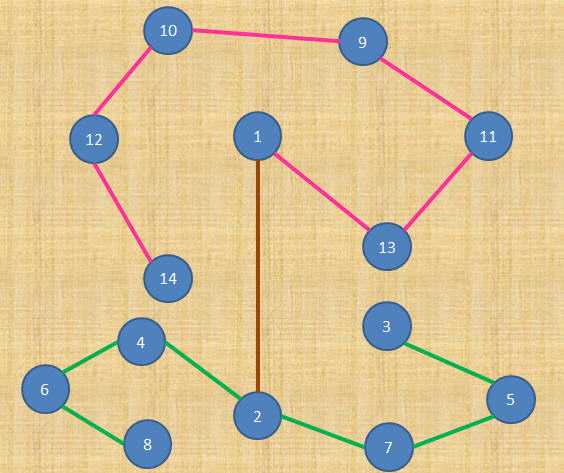
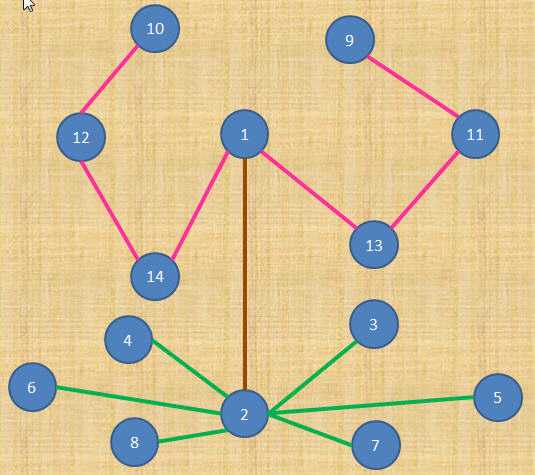
这些都是“合法的”Rose。。。
想想看，有n个顶点，如果做得出k>n-1条花边，那么我肯定可以完成玫瑰的形状了，
我们发现，每一个顶点到另一个顶点，有且只有一条路径（由花边组成的哟），没有“环”/“回路”；也就是说，不转身，就永远回不到起点。（文艺范有木有啊啊啊啊 [emoji]~）
最小生成树：
然而现实很残酷，大天朝子民在实践中探索，在劳动中突破，发现制作God‘s Rose的每一条边要用的成本是不一样滴……凝聚了中国古人智慧的“Rose资料”终于在2016年7月20日出炉啦(~^.^~)：
（单位：元）
很幸运，我也分到了一颗种子；很不幸，我是个口袋没有money的单身狗（’ ï _ ï `)。啊啊啊啊啊——【天崩地裂ing~~】——等等！
“我的大脑还能思维。”——霍金
为了尽量节省我的pocket money，以至于我既当上了Cupid，也可以有足够经费去开车，我决定寻找所有设计方案中花费最小的那一种。在所有生成树中，边权总和最小的生成树，这就是“最小生成树”！！！
我跑去求程序猿小A。“啊~给你Prim算法和Kruskal算法吧！我全家都用它！”//%% MTCheng all rights reserved %%//
//=====================^_^=顽皮的分割线=^_^===================\\
Prim算法：
假设我要从花心（即点1）开始制作这朵玫瑰，老司机会对我说：
“假设G=(V,E)是一个具有n个顶点的带权连通无向图,T=(U,TE)是G的最小生成树,其中U是T的顶点集,TE是T的边集,则由G构造最小生成树T的步骤如下：
(1) 初始化U={v0}。v0到其他顶点的所有边为候选边；
(2) 重复以下步骤n-1次,使得其他n-1个顶点被加入到U中：
① 从候选边中挑选权值最小的边输出,设该边在V-U中的顶点是v,将v加入U中,删除和v关联的边；
② 考察当前V-U中的所有顶点vi,修改候选边：若(v,vi)的权值小于原来和vi关联的候选边,则用(v,vi)取代后者作为候选边。”
是不是太枯燥了……？
//%% MTCheng all rights reserved %%//
首先，我们先把花心用金色颜料涂上（这个不费钱），那么，为了保持玫瑰制作时不会受地心引力而分裂，我们决定下一步先看看那些是 “一头涂好金色颜料，一头没有碰过” 的花边：
1.emm~~需要观察的边大约被我连接起来了。为了让我的预算一定是最小的，我决定找这些花边中，制作费最便宜的那条，即连接1-9的cost me 9438 元的那条花边，并且把边上的点也一起涂成金黄色，已经换作用金子铺的了。
2.好吧，按一下F5刷新连接，看看现在有哪些是“一头涂好金色颜料，一头没有碰过” 的花边//%% MTCheng all rights reserved %%//，再找到一条制作费最便宜的，即1-10 cost me 11438 元的那条花边，再把需要的东西涂色、填充。天啦，又花费了我大把的金子了啊(,º_º,)……
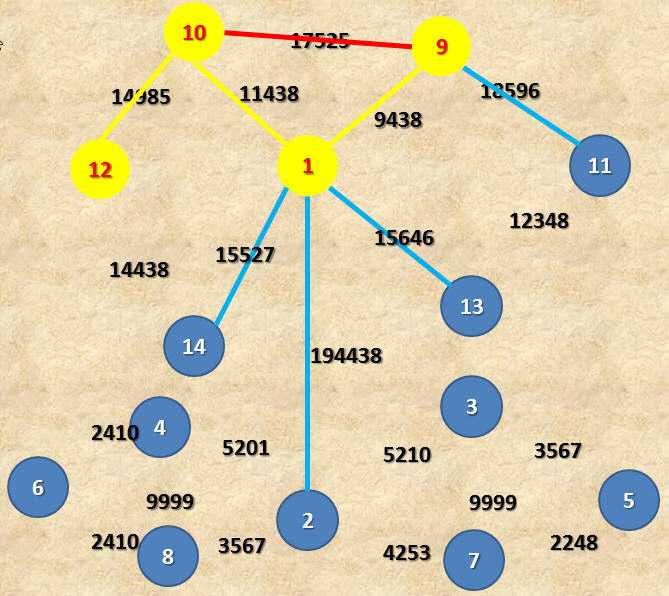
3~n .重复与1或2相同的做法，也就是说，会不停地有花边因为我们新涂色了几个点而进入视野，也不停地有花边因为连接了两个金色点而被刷掉……
1.
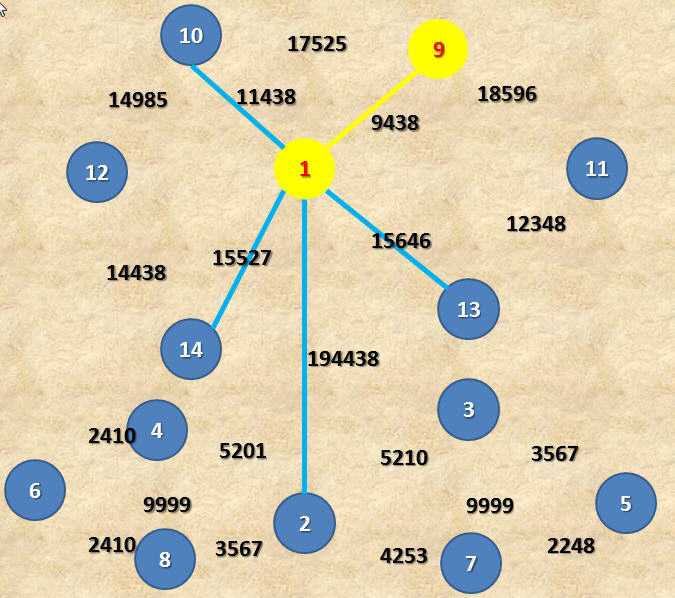2.
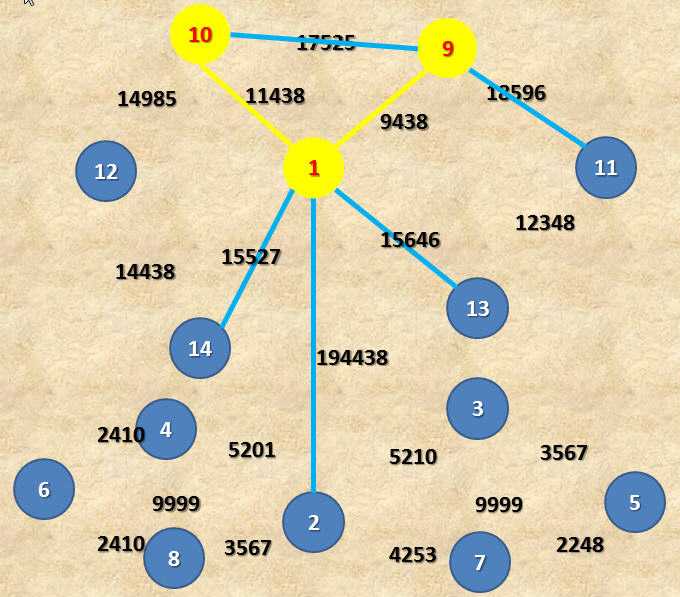3.
void Prim(int m[][MAXV],int nv,int begin) { int closest[MAXV];//c[i]=k记录i在最小生成树中的前驱结点是k int lowcost[MAXV];//l[i]=v记录了从节点i到已知树上任何一个节点的最小距离为v int i,j,min,k; for(i=0;i<nv;i++)//初始化为树中存在begin节点的状态 { closest[i]=begin; lowcost[i]=m[begin][i];//这棵树就是只已知begin嘛~~ } for(i=1;i<nv;i++) { min=INF; for(j=0;j<nv;j++) { if(lowcost[j]!=0&&lowcost[j]<min)//寻找出所有节点中非树的节点与已知树的最短距离 //lowcost[j]!=0证明此节点非树节点，lowcost[j]<min则表明当前j离树最近 { min=lowcost[j]; k=j;//来个k作为替身吧 } } //输出边咯~(ò. ó)~//###################################################### printf("Prim %d -> %d = %d\n",closest[k]+1,k+1,m[closest[k]][k]); lowcost[k]=0;//表明k已经在树上了 for(j=0;j<nv;j++) { if(m[k][j]!=0&&m[k][j]<lowcost[j]) /*m[k][j]!=0说明不是无用点（k==j） m[k][j]<lowcost[j]说明在之前的节点Finish以下工作以后， 树上新的k节点比之前的节点 离节点j都要近 */ { lowcost[j]=m[k][j]; closest[j]=k; } } } return ; }
//%% MTCheng all rights reserved %%// int main() { int nv;//the number of Vertexes int ne;//the number of Edges int m[MAXV][MAXV]; int i,j; int x,y,w; //Read in the graph scanf("%d%d",&nv,&ne); for(i=0;i<nv;i++) m[i][i]=0; for(i=0;i<ne;i++) { scanf("%d%d%d",&x,&y,&w); m[x][y]=w; m[y][x]=w; } //Do ~ ~ Prim(m,nv,0); }
To be Continue~~
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 #define INF 32767 5 #define MAXV 20 6 typedef struct edge 7 { 8 int from,to; 9 int weight; 10 }sE; 11 12 void print(int m[][MAXV]) 13 { 14 int i,j; 15 for(i=0;i<8;i++) 16 { 17 for(j=0;j<8;j++) 18 { 19 printf("%d-%d %d ",i,j,m[i][j]); 20 } 21 printf("\n"); 22 } 23 return ; 24 } 25 int cmp(const void *a,const void *b) 26 { 27 sE c=*(sE *)a; 28 sE d=*(sE *)b; 29 if(c.weight<d.weight)return -1; 30 else if(c.weight==d.weight)return 0; 31 else return 1; 32 } 33 int findx(int *fx,int x) 34 { 35 while(fx[x]!=x) 36 x=fx[x]; 37 return x; 38 } 39 void Kruskal(int m[][MAXV],int nv,int ne,int begin) 40 { 41 sE e[ne]; 42 int fx[nv]; 43 int lene=0; 44 int i,j; 45 int r1,r2; 46 for(i=0;i<nv;i++) 47 { 48 fx[i]=i;//顺便初始化并查集 49 for(j=i;j<nv;j++) 50 { 51 if(m[i][j]!=INF&&m[i][j]!=0)//将邻接矩阵转化成边 52 { 53 e[lene].from=i; 54 e[lene].to=j; 55 e[lene].weight=m[i][j]; 56 ++lene; 57 } 58 } 59 } 60 qsort(e,ne,sizeof(e[0]),cmp); 61 62 j=0; 63 for(i=0;j<nv&&i<ne;i++) 64 { 65 r1=findx(fx,e[i].from); 66 r2=findx(fx,e[i].to); 67 if(r1!=r2)//此边可以使用 68 { 69 //输出边咯~(ò^ ó)~//###################################################### 70 printf("Kruskal %d -> %d = %d\n",e[i].from+1,e[i].to+1,e[i].weight); 71 fx[r1]=r2; 72 j++; 73 } 74 //否则若加入此边 则出现回路 75 } 76 return ; 77 } 78 void Prim(int m[][MAXV],int nv,int begin) 79 { 80 int closest[MAXV];//c[i]=k记录i在最小生成树中的前驱结点是k 81 int lowcost[MAXV];//l[i]=v记录了从节点i到已知树上任何一个节点的最小距离为v 82 int i,j,min,k; 83 for(i=0;i<nv;i++)//初始化为树中存在begin节点的状态 84 { 85 closest[i]=begin; 86 lowcost[i]=m[begin][i];//这棵树就是只已知begin嘛~~ 87 } 88 for(i=1;i<nv;i++) 89 { 90 min=INF; 91 for(j=0;j<nv;j++) 92 { 93 if(lowcost[j]!=0&&lowcost[j]<min)//寻找出所有节点中非树的节点与已知树的最短距离 94 //lowcost[j]!=0证明此节点非树节点，lowcost[j]<min则表明当前j离树最近 95 { 96 min=lowcost[j]; 97 k=j;//来个k作为替身吧 98 } 99 } 100 //输出边咯~(ò. ó)~//###################################################### 101 printf("Prim %d -> %d = %d\n",closest[k]+1,k+1,m[closest[k]][k]); 102 103 lowcost[k]=0;//表明k已经在树上了 104 for(j=0;j<nv;j++) 105 { 106 if(m[k][j]!=0&&m[k][j]<lowcost[j]) 107 /*m[k][j]!=0说明不是无用点（k==j） 108 m[k][j]<lowcost[j]说明在之前的节点Finish以下工作以后， 109 树上新的k节点比之前的节点 离节点j都要近 110 */ 111 { 112 lowcost[j]=m[k][j]; 113 closest[j]=k; 114 } 115 } 116 } 117 118 return ; 119 } 120 int main() 121 { 122 int nv;//the number of Vertexes 123 int ne;//the number of Edges 124 int m[MAXV][MAXV]; 125 int i,j; 126 int x,y,w; 127 scanf("%d%d",&nv,&ne); 128 for(i=0;i<nv;i++) 129 m[i][i]=0; 130 for(i=0;i<ne;i++) 131 { 132 scanf("%d%d%d",&x,&y,&w); 133 m[x][y]=w; 134 m[y][x]=w; 135 } 136 Prim(m,nv,0); 137 Kruskal(m,nv,ne,0); 138 }
我的口水话：最小生成树、Prim、Kruskal算法是什么？
标签：社会主义 dwr ns3 atq baidu jid gdk sae lap
原文地址：http://www.cnblogs.com/MicoTimlesCheng/p/5689574.html
