标签:pre 误差 表示 return 技术 ble clu nbsp 大致
题目:
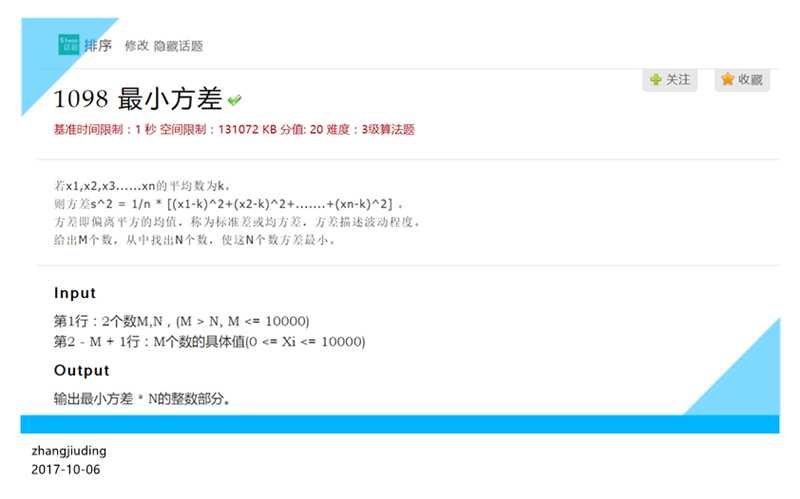
题目要我们,在m个数中,选取n个数,求出这n个数的方差,求方差的最小值。
1.我们知道,方差是描述稳定程度的,所以肯定是着n个数越密集,方差越小。
所以我们给这m个数排个序,从连续的n个数中找。
2.方差公式D(x^2) = E(x^2)- E(x)^2;
E(x) = x*f(x) dx (从负无穷到正无穷积分)
E (x^2) = x^2*f(x) dx (从负无穷到正无穷积分)
3.对于这道题,相当于每个数的权值相同,也就是f(x)相同,都等于1/n。(可以理解f(x)表示概率)
4.我们可以用前缀和来减少时间复杂度。
sum1[i]表示前 i 项的和,方便算出E(x)^2
sum2[i]表示前 i 项平方和 ,方便算出E(x^2)
当我们要算第 i 项到第 j 项共 j-i+1 项的方差的时候我们只用这样写:
ll k1 = sum1[j]-sum1[i-1]; // 第i项到第j项的和 double s1 = 1.0*k1/n*k1/n; // k1/n表示平均数E(x), s1表示E(x)^2 ll k2 = sum2[j]-sum2[i-1]; // 第i项到第j项的平方和 double s2 = 1.0*k2/n; // s2 和 k2/n 表示E(x^2)
第 i 项到第 j 项的方差就等于 s2-s1 了。
5.我们可以得到大致代码,当然现在就可以直接开始敲了,如果看懂了的话。
double mn = 2e18; for(int i = n;i <= m; i++){ ll k1 = sum1[i]-sum1[i-n]; double s1 = 1.0*k1/n*k1/n; ll k2 = sum2[i]-sum2[i-n]; double s2 = 1.0*k2/n; mn = min(s2-s1,mn); }
6.我们要注意一下精度问题,我的做法是给mn += 1e-8。
代码:
#include <bits\stdc++.h> using namespace std; typedef long long ll; int a[10010]; ll sum1[10010]; //sum1[i]表示前i项和 ll sum2[10010]; //sum2[i]表示前i项平方和 int main() { ll m,n; cin >> m >> n; for(int i = 1;i <= m; i++){ cin >> a[i]; } sort(a+1,a+1+m); // 排个序,让数字变得紧凑 for(int i = 1;i <= m; i++){ sum1[i] = sum1[i-1] + a[i]; sum2[i] = sum2[i-1] + a[i]*a[i]; } double mn = 2e18; //存最小的方差 for(int i = n;i <= m; i++){ ll k1 = sum1[i]-sum1[i-n]; // 第 i-n+1 项到第 i项共 n 项的和。 double s1 = 1.0*k1/n*k1/n; // k1/n表示平均数E(x),s1表示 E(x)^2 ll k2 = sum2[i]-sum2[i-n]; // 第 i-n+1 项到第 i项共 n 项的和。 double s2 = 1.0*k2/n; // k2/n表示E(x^2) mn = min(s2-s1,mn); } // 如果不加这个可能会出问题,因为cout double用的是科学记数法,需要消除误差。 mn += 1e-8; cout << (ll)(mn*n) << endl; return 0; } // writen by zhangjiuding
标签:pre 误差 表示 return 技术 ble clu nbsp 大致
原文地址:http://www.cnblogs.com/zhangjiuding/p/7631313.html