标签:技术 out can cstring 比较 span 思路 ++ main
模板
如何在目标串中找到模式串p?
1、暴力枚举起始位置,逐位比较
缺点:枚举太多无用位置,时间复杂度高
Codes:
1 int j; 2 for(int i = 0;s[i];++ i){ 3 for(j = 0;p[j];++ j) 4 if(s[i + j] != p[j]) 5 break; 6 if(!p[j]){ //匹配成功 7 //Operations 8 } 9 }
复杂度:O((n - m + 1) * m) (n:原串长度,m:匹配串长度)
2、KMP
优点:只枚举了可能有用的位置(其实就是暴力缺点opp. QwQ)
那是如何做到只枚举有用位置的呢?
nxt数组!
①nxt[i + 1] 定义为最大的 j + 1 使得 p[0~j] 是 p[0~i] 的后缀
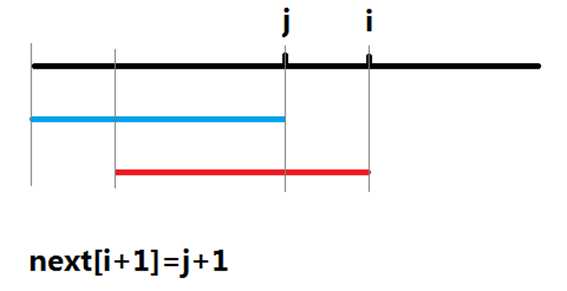
②nxt[i] 定义为当 i 位置不匹配时,将跳到 nxt[i] 位置重新匹配(关于nxt数组定义众说纷纭,这里只给出我认为最易懂的定义QwQ)
因为再不匹配时kmp算法并不是再枚举下一位,而是跳到 nxt[i] 继续匹配,所以会明显提高效率,时间复杂度降到线性
例子1:
P : 0 1 2 3 4 5 6 7
a b c a b c a d
nxt: -1 0 0 0 1 2 3 4
例子2:
P : 0 1 2 3 4 5 6 7
a b a c b a b a
nxt: -1 0 0 1 0 0 1 2
清楚定义之后,计算nxt[]的思路也差不多了
Codes:
1 void get_nxt(char *p){ 2 int i = 0,j = -1; 3 nxt[0] = -1; //边界 4 while(p[i]){ 5 if(j == -1 || p[j] == p[i]) //到达边界 或 前缀等于后缀 6 nxt[++ i] = ++ j; //可以跳到的位置 + 1 7 else j = nxt[j]; //不匹配则跳到 nxt[] 8 } 9 return; 10 }
接下来是匹配,可以观察其与暴力的不同或相同点
Codes:
1 int kmp(char *p,char *s){ //传指针,可以理解为数组 2 //s:目标串,p:模式串 3 int res = 0; //计数,出现次数 4 get_nxt(p); //处理nxt 5 for(int i = 0,j = 0;s[i];++ i){ 6 while(j != -1 && s[i] != p[j]) 7 j = nxt[j]; //若不匹配,跳到 nxt[j] 8 ++ j; //匹配上 9 if(!p[j]){ //模式串与目标串匹配完成 10 res ++; //计数 ++ 11 j = nxt[j]; //若计算重叠串则返回nxt[j] 12 //Operations 13 } 14 } 15 return res; 16 }
模板(其实就是把上面搬过来2333)
Codes:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #define N 1010 6 7 using namespace std; 8 9 char s[N],p[N]; 10 int nxt[N]; 11 void get_nxt(char *p){ 12 int i = 0,j = -1; 13 nxt[0] = -1; //边界 14 while(p[i]){ 15 if(j == -1 || p[j] == p[i]) //到达边界 或 前缀等于后缀 16 nxt[++ i] = ++ j; //可以跳到的位置 + 1 17 else j = nxt[j]; //不匹配则跳到 nxt[] 18 } 19 return; 20 } 21 int kmp(char *p,char *s){ //传指针,可以理解为数组 22 //s:目标串,p:模式串 23 int res = 0; //计数,出现次数 24 get_nxt(p); //处理nxt 25 for(int i = 0,j = 0;s[i];++ i){ 26 while(j != -1 && s[i] != p[j]) 27 j = nxt[j]; //若不匹配,跳到 nxt[j] 28 ++ j; //匹配上 29 if(!p[j]){ //模式串与目标串匹配完成 30 res ++; //计数 ++ 31 j = nxt[j]; //若计算重叠串则返回nxt[j] 32 //Operations 33 } 34 } 35 return res; 36 } 37 int main(){ 38 scanf("%s%s",s,p); 39 cout << kmp(s,p) << ‘\n‘; 40 return 0; 41 }
标签:技术 out can cstring 比较 span 思路 ++ main
原文地址:http://www.cnblogs.com/Loizbq/p/7635823.html