标签:iso insert 排序 基于 size 结果 -- 级别 ges
(1)直接插入排序:一般插入排序,比较是从有序序列的最后一个元素开始,如果比它大则直接插入在其后面,否则一直往前比。
如果找到一个和插入元素相等的,那么就插入到这个相等元素的后面。 插入排序是 稳定的。
(2)希尔排序:希尔排序是按照不同步长对元素进行插入排序,一次插入排序是稳定的,不会改变相同元素的相对顺序,
但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,稳定性就会被破坏,所以 希尔排序 不稳定。
(3)简单选择排序:在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
光说可能有点模糊,来看个小实例:858410,第一遍扫描,第1个元素8会和4交换,那么原序列中2个8的相对前后顺序和原序列不一致了,所以 选择排序 不稳定。
(4)堆排序:堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n/2-1, n/2-2, ...这些父节点选择元素时,有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1个父节点把后面一个相同的元素没有交换,所以堆排序并不稳定。
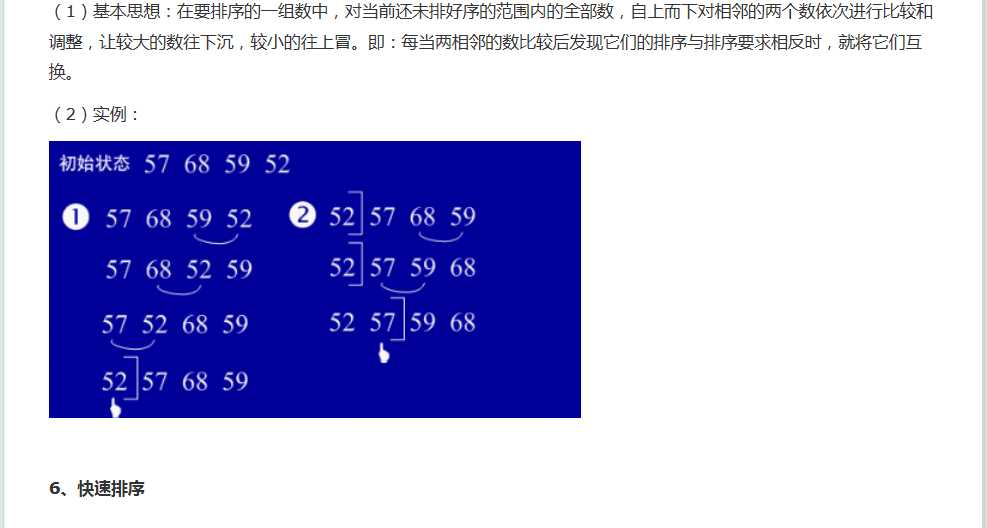
(5)冒泡排序:由前面的内容可知,冒泡排序是相邻的两个元素比较,交换也发生在这两个元素之间,如果两个元素相等,不用交换。所以冒泡排序 稳定。
(6)快速排序:在中枢元素和序列中一个元素交换的时候,很有可能把前面的元素的稳定性打乱。
还是看一个小实例:6 4 4 5 4 7 8 9,第一趟排序,中枢元素6和第三个4交换就会把元素4的原序列破坏, 所以快速排序 不稳定。
(7)归并排序:在分解的子列中,有1个或2个元素时,1个元素不会交换,2个元素如果大小相等也不会交换。
在序列合并的过程中,如果两个当前元素相等时,我们把处在前面的序列的元素保存在 结果序列 的前面,所以,归并排序也是稳定的。
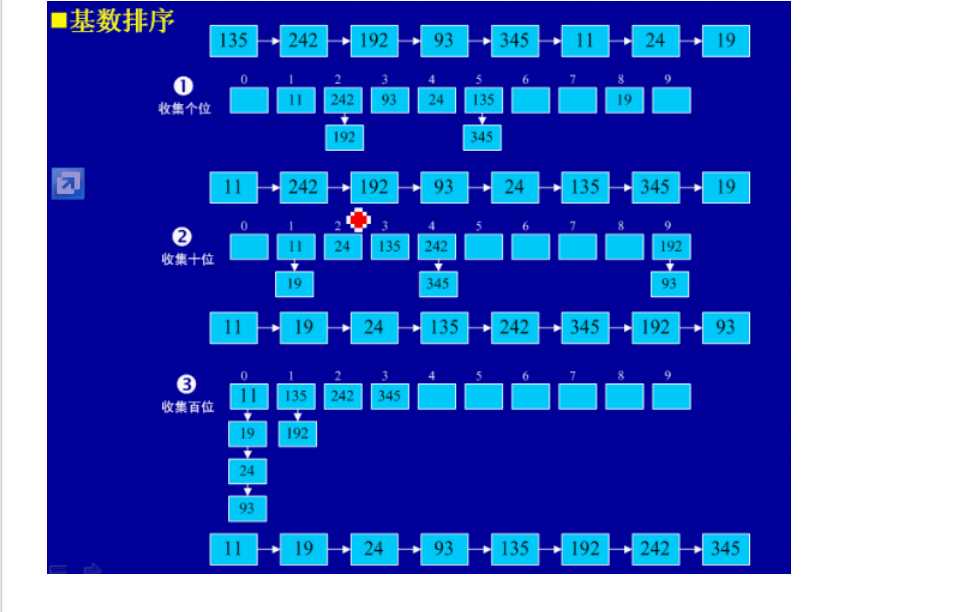
(8)基数排序:是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
8种排序的分类,稳定性,时间复杂度和空间复杂度总结:
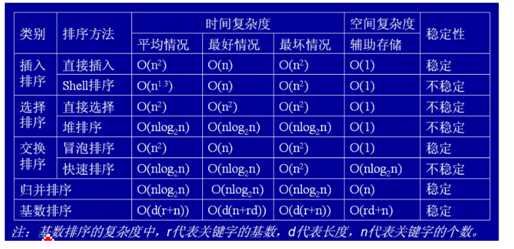
排序算法可以根据不同的特性划分为不同的类别,这些特性有:
+ 是否是 comparison-based (基于 比较)
+ 时间复杂度: O(nlogn) 级别还是 O(n^2)级别
+ 空间复杂度
+ 是否 stable, 即维持原有相对顺序
+ 是否 adaptive, 即算法时间是否与输入序列的有序性相关
comparison-based 排序算法
1. 插入排序(Insertion Sort) - O(n^2)
1)算法描述: 给定一个序列, 假设当前处理位置 p, p 之前的子序列是已经被排序的, 那么当前只要把 data[p] 插入到 data[1~p-1] 合适的位置, 先比较 p 和 p-1, 如有必要, 再和 p-2 比较.
2)时间: 平均 O(n^2) 的, 最好 O(n) -- 输入序列已排序, 最差 O(n^2) -- 输入序列逆序.
3)空间: O(1). stable: 根据算法描述不难得知它是 stable 的.
4) online: 该算法也是在线的, 对于输入流中新入的每一个数字 d, 只要将 d 插入到已有的排序序列中即可.
2.选择排序(Selection Sort) - O(n^2)
1)算法描述: 给定一个序列, 每次扫描未排序的部分, 选出最小的元素, 将它写入已经排序的部分.
2)时间: O(n^2), 不管输入序列是否有序, 该算法都需要 O(n^2) 次比较.
3)空间: O(1). stable: 算法会交换当前值和最小值, 这会破坏序列的稳定性.
4)online: 易知算法做不到在线, 因为假如新入的数字是最小的, 算法不能将它插入到序列的首位.
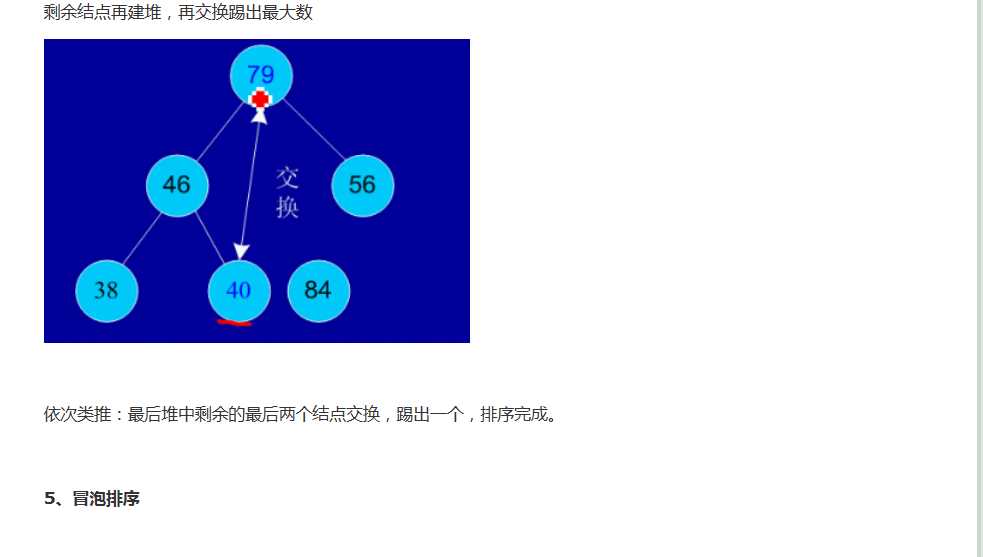
3.冒泡排序(Bubble Sort) - O(n^2)
1)算法描述: 给定一个序列, 每次都从首位开始 "冒泡", 比较并交换(如必要)相邻的两个元素, 直到当前的结尾. 每一轮冒泡都将当前的最大值放到当前的结尾.
2)时间: 平均 O(n^2), 最好 O(n) -- 输入序列已排序, 最差 O(n^2) -- 输入序列逆序.
3)空间: O(1). stable: 是的.
4)online: 可以想象该算法不适合在线.
5)备注: 该算法实际中效果较差, 但有一点值得借鉴, 便是判断序列是否已排序 -- 扫描序列, 确认没有逆序对.
4.希尔排序(Shell Sort) - O(n(logn)^2) / O(n^3/2)
1)算法描述: 有一个间隔序列, 排序 data[i], data[i+gap] 子序列, 当排序最后间隔为 1 的子序列之后, 原始序列便被排序.
2)时间: 平均 O(n(logn)^2) 或 O(n^3/2), 最好 O(n), 最坏 O(n^2) -- 该算法时间复杂度的证明很复杂.
3)空间: O(1).
4)stable: 不是.
5)online: 显然不是.
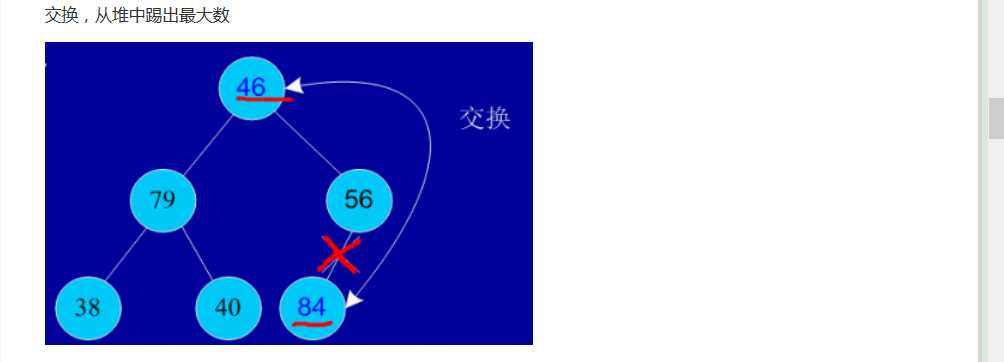
5.堆排序(Heap Sort) - O(nlogn)
1)算法描述: 利用最大堆的思想来排序.
2)时间: 该算法的优点是有稳定的运行时间 O(nlogn).
3)空间: O(1) , 如在数组实现中, 利用数组末尾存储已排序的数字.
4)stable: 不是.
5)online:
6.归并排序(Merge Sort) - O(nlogn)
1)算法描述: 将输入序列递归地划分为子序列, 长度为 1 的子序列被认为是已排序的, 然后合并已排序的子序列.
2)时间: O(nlogn).
3)空间: 最坏的情况是 O(n).
备注: 该算法有两种实现方式, top-down 和 bottom-up.
7.快速排序(Qcuik Sort) - O(nlogn)
1)算法描述: 对于给定序列, 选取一个 pivot, 将大于该 pivot 的放在其右侧, 小于等于的放于 pivot 左侧. 递归地处理左右侧的子序列.
2)时间: O(nlogn), 最坏情况 O(n^2).
3)空间: stable: online:
备注:
不是 comparison-based 的排序算法







标签:iso insert 排序 基于 size 结果 -- 级别 ges
原文地址:http://www.cnblogs.com/wangprince2017/p/7658527.html