标签：logs x11 大小 黄色 三次 未来 因此 多项式 9.png
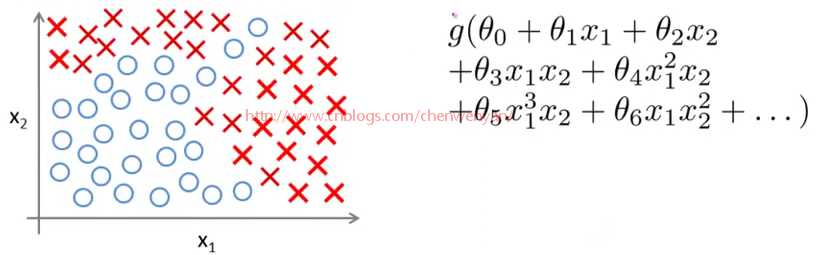
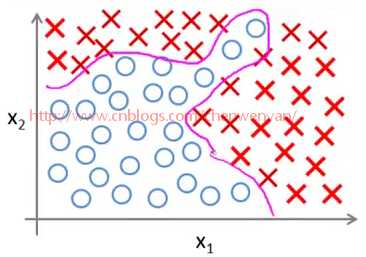
如上图所示，如果用逻辑回归来解决这个问题，首先需要构造一个包含很多非线性项的逻辑回归函数g(x)。这里g仍是s型函数（即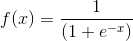
）。我们能让函数包含很多像这的多项式，当多项式足够多时，那么你也许能够得到可以分开正样本和负样本的分界线，如图下粉红色分界线所示：
当只有两项时，比如x1、x2,这种方法能够得到不错的效果，因为你可以把x1和x2的所有组合都包含到多项式中，但是对于许多复杂的机器学习问题涉及的项往往多于两项，以房屋为例，影响房屋价格因素有房子大小、卧室数量、楼层、房龄等等。假设现在要处理的是关于住房的分类问题，则不再是一个回归问题。假设你对一栋房子的多方面特点都有所了解，你想预测房子在未来半年内能被卖出去的概率，这是一个分类问题，我们可以想出有很多特征向量对于不同的房子的影响。
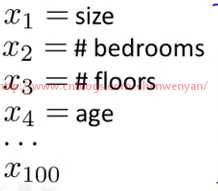
对于这类问题，如果要包含所有的二次项，即使只包含二项式或多项式的计算, 最终的多项式也可能有很多项，比如x1^2, x1x2,x1x3,x1x4，直到x1x100, 还有x2^2, x2x3……，因此，即使只考虑二阶项，也就是说，两个项的乘积，x1乘以x1，等等类似于此的项，那么，在n=100的情况下，最终也有5000个二次项。而且渐渐地，随着特征个数n的增加，二次项的个数大约以n^2的量级增长，其中，n是原始项的个数，即我们之前说过的x1到x100这些项，事实上二次项的个数大约是(n^2)/2, 因此要包含所有的二次项是很困难的, 所以这可能不是一个好的做法, 而且由于项数过多, 最后的结果很有可能是过拟合的。此外，在处理这么多项时，也存在运算量过大的问题，当然，你也可以试试只包含上边这些二次项的子集。例如，我们只考虑，x1^2,x2^2,x3^2……x100^2, 这样就可以将二次项的数量大幅度减少, 减少到只有100个二次项, 但是由于忽略了太多相关项, 在处理类似第一张图的数据时，不可能得到理想的结果。实际上，如果只考虑x1的平方到x100的平方这一百个二次项，那么你可能会拟合出一些特别的假设，比如可能拟合出一个椭圆的形状，但是肯定不能拟合出像第一张图这个数据集的分界线。所以5000个二次项看起来已经很多了，而现在假设包括三次项或者三阶项例如x1x2x3,(x1^2)x2,x10x11x17……类似的三次项有很多很多。事实上，三次项的个数是以n^3的量级增加，当n=100时，可以计算出来，最后能得到，大概17000个三次项，所以当初始特征个数n增大时，这些高阶多项式项数将以几何级数递增，特征空间也随之急剧膨胀, 当特征个数n很大时, 如果找出附加项来建立一些分类器, 这并不是一个好做法, 对于许多实际的机器学习问题,特征个数n是很大的。以下是一个例子：
关于计算机视觉中的一个问题，假设你想要使用机器学习算法来训练一个分类器，使它检测一个图像来判断图像是否为一辆汽车。很多人可能会好奇，这对计算机视觉来说有什么难的。当我们自己看这幅图像时，里面有什么是一目了然的事情，你肯定会很奇怪，为什么学习算法竟可能会不知道图像是什么。为了解答这个问题，我们取出这幅图片中的一小部分，将其放大，比如图下这个红色方框内的部分。
结果表明当人眼看到一辆汽车时，计算机实际上看到的却是一个数据矩阵或像这种格网，如下图所示：
它们表示了像素强度值，告诉我们图像中每个像素的亮度值。因此，对于计算机视觉来说，问题就变成了根据这个像素点亮度矩阵，来告诉我们这些数值代表一个汽车门把手。具体而言，当用机器学习算法构造一个汽车识别器时，我们要想出一个带标签的样本集，其中一些样本是各类汽车，另一部分样本是其他任何东西，如下图所示：
将这个样本集输入给学习算法，以训练出一个分类器，训练完毕后，输入一幅新的图片让分类器判定“这是什么东西？”。理想情况下，分类器能识别出这是一辆汽车。为了理解引入非线性分类器的必要性，我们从学习算法的训练样本中，挑出一些汽车图片和一些非汽车图片。从其中每幅图片中挑出一组像素点，像素点1、像素点2的位置如图下所示，在坐标系中标出这幅汽车的位置。在某一点上，车的位置取决于像素点1和像素点2的亮度。
用同样的方法标出其他图片中汽车的位置，然后我们再举一个关于汽车的不同的例子，观察这两个相同的像素位置，图下橘黄色小车中像素1有一个像素强度，像素2也有一个不同的像素强度，所以在这幅图中它们两个处于不同的位置。我们继续画上两个非汽车样本（负号表示的样本），然后我们继续在坐标系中画上更多的新样本，用‘‘+"表示汽车图片，用“-”表示非汽车图片。
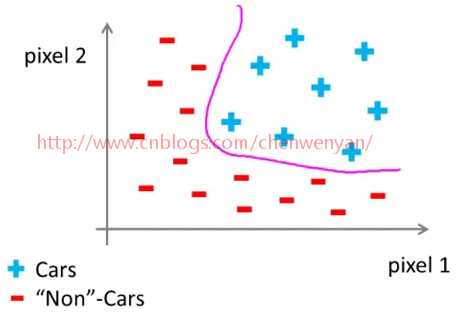
我们将发现汽车样本和非汽车样本，分布在坐标系中的不同区域。我们现在需要一个非线性分类器，尽量分开这两类样本。这个分类问题中特征空间的维数是多少？假设我们用50*50像素的图片，但这依然是2500个像素点，因此我们的特征向量的元素数量N = 2500。特征向量X包含了所有像素点的亮度值，左边是像素点1的亮度，右边是像素点2的亮度。如此类推，直到最后一个像素点的亮度，对于典型的计算机图片表示方法，如果存储的是每个像素点的灰度值（色彩的强烈程度），那么每个元素的值应该在0到255之间。因此，这个问题中n=2500，但是这只是使用灰度图片的情况。如果我们用的是RGB彩色图像，每个像素点包含红、绿、蓝三个子像素，那么n=7500。因此，如果我们非要通过包含所有的二次项来解决这个非线性问题，那么下面式子中的所有条件xi*xj，连同开始的2500像素，总共大约有300万个。这数字大得有点离谱了，对于每个样本来说，要发现并表示所有这300万个项，这计算成本太高了。
因此，只是简单的增加二次项或者三次项之类的逻辑回归算法，并不是一个解决复杂非线性问题的好办法。因为当n很大时，将会产生非常多的特征项。因此神经网络在解决复杂的非线性分类问题上被证明是是一种好得多的算法，即使你输入特征空间或输入的特征维数n很大也能轻松搞定。
斯坦福大学公开课机器学习：Neural Networks，representation: non-linear hypotheses（为什么需要做非线性分类器）
标签：logs x11 大小 黄色 三次 未来 因此 多项式 9.png
原文地址：http://www.cnblogs.com/chenwenyan/p/7707189.html
