标签:进入 代码 它的 之间 相对 方式 方向 思想 重复数
一、冒泡排序
原理为两两交换,大数据就慢慢往一个方向移动,就像水里的泡泡一样,该排序很简单,无需多言。
上代码:
1 #include <stdio.h> 2 3 void bubbleSort(int arr[],int len) 4 { 5 int i,j; 6 for(i = 0; i < len - 1; ++i) 7 { 8 for(j = 0; j < len -1 - i; ++j)//已经选出的数据不用再进行排序 9 { 10 if(arr[j] > arr[j+1]) 11 { 12 int tmp = arr[j]; 13 arr[j] = arr[j+1]; 14 arr[j+1] = tmp; 15 } 16 } 17 } 18 } 19 20 void Show(int arr[],int len) 21 { 22 for(int i = 0; i < len; i++) 23 { 24 printf("%d ",arr[i]); 25 } 26 printf("\n"); 27 28 } 29 int main () 30 { 31 int arr[] = {-1,12,3,44,3,52,6,23,43,32,24,67,5,10,1,21}; 32 int len = sizeof(arr)/sizeof(arr[0]); 33 34 bubbleSort(arr,len); 35 Show(arr,len); 36 return 0; 37 }
冒泡排序总结:
时间复杂度:平均情况O(n2),最好情况O(n),最坏情况O(n2)
空间度杂度:O(1)
稳定性:稳定
而我要说的另一个交换类的排序,就复杂得多了----快速排序。
二、快速排序
快速排序,名字既然就敢这么叫,快肯定就是它的优点,天下武功,唯快不破,既然如此,我们好好研究一下。
先上图:
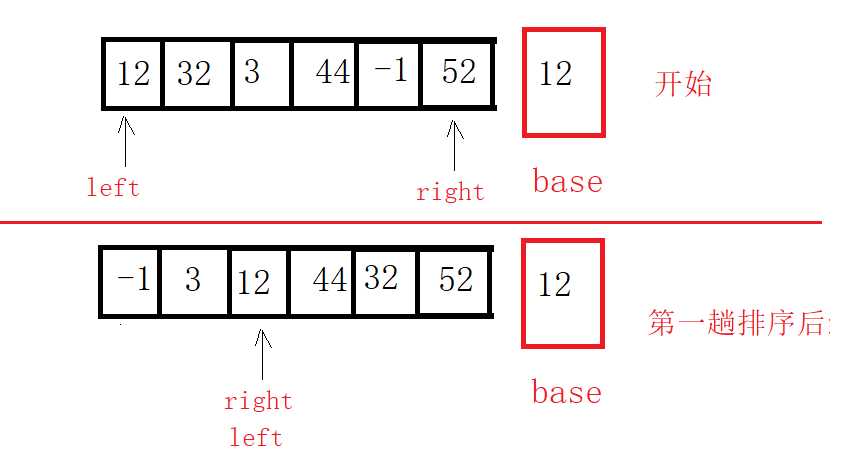
从图中我们可以看到:
left指针,right指针,base参照数。
其实思想是蛮简单的,就是通过第一遍的遍历(让left和right指针重合)来找到数组的切割点。
第一步:首先我们从数组的left位置取出该数(12)作为基准(base)参照物。
第二步:从数组的right位置向前找,一直找到比base小的数,
如果找到,将此数赋给left位置(也就是将-1赋给12),
此时数组为:-1,3,12,32,44,52
left和right指针分别为前后的-1。
第三步:从数组的left位置向后找,一直找到比(base)大的数,
如果找到,将此数赋给right的位置(也就是32赋给-1),
此时数组为:-1,32,44,32,52,
left和right指针分别为前后的32。
第四步:重复“第二,第三“步骤,直到left和right指针重合,
最后将(base)插入到40的位置,
此时数组值为: -1,32,4,32,52,至此完成一次排序。
第五步:此时12已经潜入到数组的内部,12的左侧一组数都比12小,12的右侧作为一组数都比20大,
以12为切入点对左右两边数按照"第一,第二,第三,第四"步骤递归进行,最终快排大功告成。
int Partition(int arr[],int low,int high)//返回关键字 { int i = low; int j = high; int tmp = arr[i]; while(i < j) { while(i < j && arr[j] >= tmp) j--; arr[i] = arr[j]; while(i < j && arr[i] <= tmp) i++; arr[j] = arr[i]; } arr[i] = tmp; return i; } void quickSort(int arr[],int low,int high)//快速排序,递归实现 { if(low < high) { int key; key = Partition(arr,low,high); quickSort(arr,low,key - 1); quickSort(arr,key + 1,high); } }
三、快排的优化
先来看看最普通的快排总结:
时间复杂度:平均情况O(nlog2n),最好情况O(nlog2n),最坏情况O(n2)
空间复杂度:O(nlog2n)
稳定性:不稳定
快排的缺点是不稳定,并且在不断的递归中,会开辟大量的栈空间从而造成有一定的空间复杂度。
可以看到快速排序具有很好的平均性能,但最坏的事件复杂度和插入排序相同,也是O(n^2)。比如一个序列5,4,3,2,1,要排为1,2,3,4,5。按照快速排序方法,每次只会有一个数据进入正确顺序,不能把数据分成大小相当的两份,很明显,排序的过程就成了一个歪脖子树,树的深度为n,那时间复杂度就成了O(n^2)。所以,我们只需要尽最大努力让初始序列为乱序的,自然性能就保证了。
1、 选择基准元的方式
对于分治算法,当每次划分时,算法若都能分成两个等长的子序列时,那么分治算法效率会达到最大。也就是说,基准的选择是很重要的。选择基准的方式决定了两个分割后两个子序列的长度,进而对整个算法的效率产生决定性影响。
最理想的方法是,选择的基准恰好能把待排序序列分成两个等长的子序列。(实际执行很难)
方法一:固定基准元(基本的快速排序)
思想:取序列的第一个或最后一个元素作为基准元。
如果输入序列是随机的,处理时间可以接受的。如果数组已经有序时,此时的分割就是一个非常不好的分割。因为每次划分只能使待排序序列减一,此时为最坏情况,快速排序沦为冒泡排序,时间复杂度为Θ(n^2)。而且,输入的数据是有序或部分有序的情况是相当常见的。因此,使用第一个元素作为基准元是非常糟糕的,为了避免这个情况,就引入了下面两个获取基准的方法。
方法二:随机基准元
思想:取待排序列中任意一个元素作为基准元。
引入的原因:在待排序列是部分有序时,固定选取基准元使快排效率底下,要缓解这种情况,就引入了随机选取基准元。
这是一种相对安全的策略。由于基准元的位置是随机的,那么产生的分割也不会总是会出现劣质的分割。在整个数组数字全相等时,仍然是最坏情况,时间复杂度是O(n^2)。实际上,随机化快速排序得到理论最坏情况的可能性仅为1/(2^n)。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn)的期望时间复杂度。一位前辈做出了一个精辟的总结:“随机化快速排序可以满足一个人一辈子的人品需求。”
方法三:三数取中
引入的原因:虽然随机选取基准时,减少出现不好分割的几率,但是还是最坏情况下还是O(n^2),要缓解这种情况,就引入了三数取中选取基准。
分析:最佳的划分是将待排序的序列分成等长的子序列,最佳的状态我们可以使用序列的中间的值,也就是第N/2个数。可是,这很难算出来,并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为基准元而得到。事实上,随机性并没有多大的帮助,因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为基准元。显然使用三数中值分割法消除了预排序输入的不好情形,并且减少快排大约14%的比较次数。
举例:待排序序列为:8 1 4 9 6 3 5 2 7 0
左边为:8,右边为0,中间为6
我们这里取三个数排序后,中间那个数作为枢轴,则枢轴为6
注意:在选取中轴值时,可以从由左中右三个中选取扩大到五个元素中或者更多元素中选取,一般的,会有(2t+1)平均分区法(median-of-(2t+1),三平均分区法英文为median-of-three。
具体思想:对待排序序列中low、mid、high三个位置上数据进行排序,取他们中间的那个数据作为基准,并用0下标元素存储基准。
2、两种优化的方法
优化一:当待排序序列的长度分割到一定大小后,使用插入排序
原因:对于很小和部分有序的数组,快排不如插排好。当待排序序列的长度分割到一定大小后,继续分割的效率比插入排序要差,此时可以使用插排而不是快排。
截止范围:待排序序列长度N = 10,虽然在5~20之间任一截止范围都有可能产生类似的结果,这种做法也避免了一些有害的退化情形。
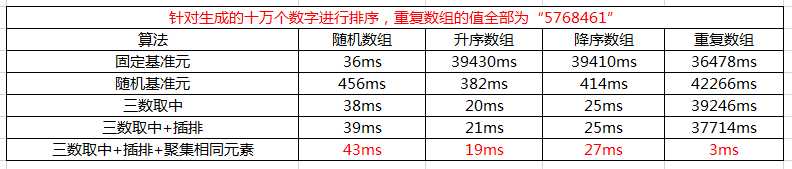
针对随机数组,使用三数取中选择基准+插排,效率还是可以提高一点,真是针对已排序的数组,是没有任何用处的。因为待排序序列是已经有序的,那么每次划分只能使待排序序列减一。此时,插排是发挥不了作用的。所以这里看不到时间的减少。另外,三数取中选择基准+插排还是不能处理重复数组。
优化二:在一次分割结束后,可以把与Key相等的元素聚在一起,继续下次分割时,不用再对与key相等元素分割
举例:
待排序序列 1 4 6 7 6 6 7 6 8 6
三数取中选取基准:下标为4的数6
转换后,待分割序列:6 4 6 7 1 6 7 6 8 6
基准key:6
本次划分后,未对与key元素相等处理的结果:1 4 6 6 7 6 7 6 8 6
下次的两个子序列为:1 4 6 和 7 6 7 6 8 6
本次划分后,对与key元素相等处理的结果:1 4 6 6 6 6 6 7 8 7
下次的两个子序列为:1 4 和 7 8 7
经过对比,我们可以看出,在一次划分后,把与key相等的元素聚在一起,能减少迭代次数,效率会提高不少
具体过程:在处理过程中,会有两个步骤
第一步,在划分过程中,把与key相等元素放入数组的两端
第二步,划分结束后,把与key相等的元素移到枢轴周围
标签:进入 代码 它的 之间 相对 方式 方向 思想 重复数
原文地址:http://www.cnblogs.com/jian-99/p/7706932.html