标签:规则 cal 树模型 实验 连续 树形结构 diff 重要 机器学习算法
调频96.8有一种游戏:游戏中,出题者写下一件东西,其他人需要猜出这件东西是什么。当然,如果游戏规则仅此而已的话,几乎是无法猜出来的,因为问题的规模太大了。为了降低游戏的难度,答题者可以向出题者问问题,而出题者必须准确回答是或者否,答题者依据回答提出下一个问题,如果能够在指定次数内确定谜底,即为胜出。
我们先实验一下,现在我已经写下了一个物体,而你和我的问答记录如下:
是男的吗?Y
是亚洲人吗?Y
是中国人吗?N
是印度人吗?Y
……
在上面的游戏中,我们针对性的提出问题,每一个问题都可以将我们的答案范围缩小,在提问中和回答者有相同知识背景的前提下,得出答案的难度比我们想象的要小很多。
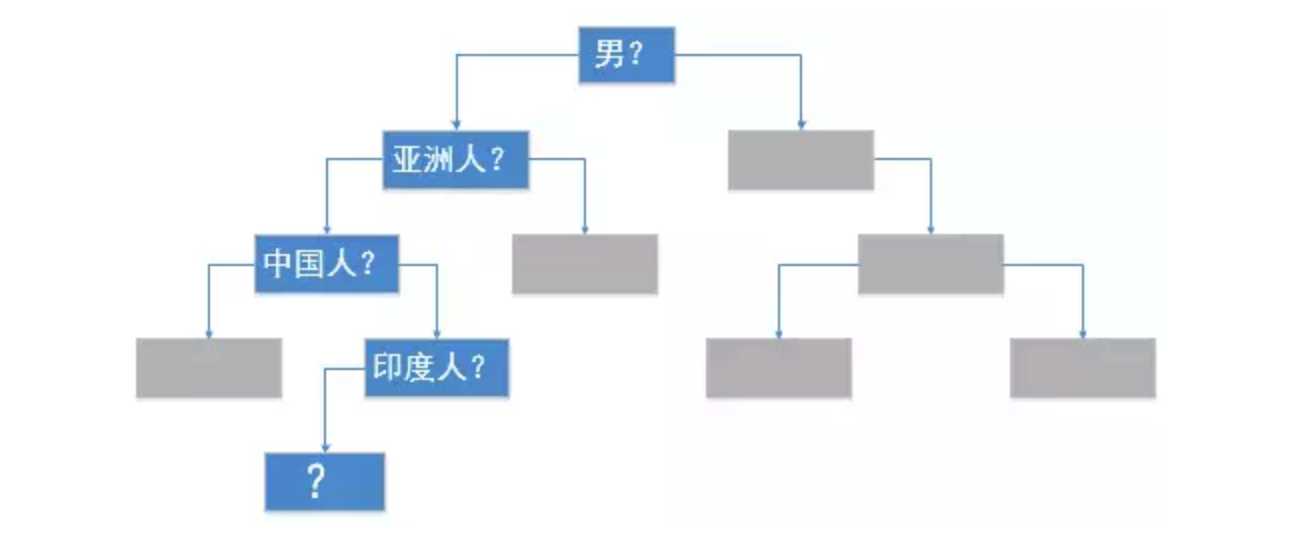
在每一个节点,依据问题答案,可以将答案划分为左右两个分支,左分支代表的是Yes,右分支代表的是No,虽然为了简化,我们只画出了其中的一条路径,但是也可以明显看出这是一个树形结构,这便是决策树的原型。
我们面对的样本通常具有很多个特征,正所谓对事物的判断不能只从一个角度,那如何结合不同的特征呢?决策树算法的思想是,先从一个特征入手,就如同我们上面的游戏中一样,既然无法直接分类,那就先根据一个特征进行分类,虽然分类结果达不到理想效果,但是通过这次分类,我们的问题规模变小了,同时分类后的子集相比原来的样本集更加易于分类了。然后针对上一次分类后的样本子集,重复这个过程。在理想的情况下,经过多层的决策分类,我们将得到完全纯净的子集,也就是每一个子集中的样本都属于同一个分类。 由这个分类的过程形成一个树形的判决模型,树的每一个非叶子节点都是一个特征分割点,叶子节点是最终的决策分类。
上面我们介绍决策树算法的思想,可以简单归纳为如下两点:
每次选择其中一个特征对样本集进行分类
对分类后的子集递归进行步骤1
在第一个步骤中,我们需要考虑的一个最重要的策略是,选取什么样的特征可以实现最好的分类效果,而所谓的分类效果好坏,必然也需要一个评价的指标。
直观来说就是集合中样本所属类别比较集中,最理想的是样本都属于同一个分类。样本集的纯度可以用熵来进行衡量。
在信息论中,熵代表了一个系统的混乱程度,熵越大,说明我们的数据集纯度越低,当我们的数据集都是同一个类别的时候,熵为0,熵的计算公式如下:
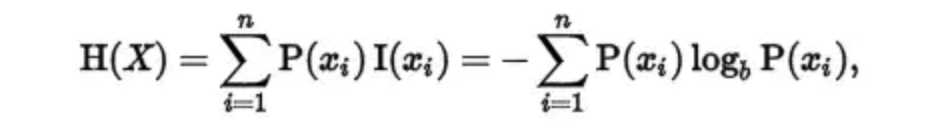
其中,P(xi)表示概率,b在此处取2。比如抛硬币的时候,正面的概率就是1/2,反面的概率也是1/2,那么这个过程的熵为:
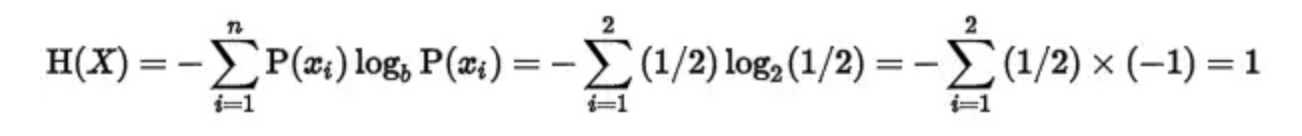
可见,由于抛硬币是一个完全随机事件,其结果正面和反面是等概率的,所以具有很高的熵。
假如我们观察的是硬币最终飞行的方向,那么硬币最后往下落的概率是1,往天上飞的概率是0,带入上面的公式中,可以得到这个过程的熵为0,所以,熵越小,结果的可预测性就越强。在决策树的生成过程中,我们的目标就是要划分后的子集中其熵最小,这样后续的的迭代中,就更容易对其进行分类。
既然是递归过程,那么就需要制定递归的停止规则。
在两种情况下我们停止进一步对子集进行划分,其一是划分已经达到可以理想效果了,另外一种就是进一步划分收效甚微,不值得再继续了。
用专业术语总结终止条件有以下几个:
子集的熵达到阈值
子集规模够小
进一步划分的增益小于阈值
其中,条件3中的增益代表的是一次划分对数据纯度的提升效果,也就是划分以后,熵减少越多,说明增益越大,那么这次划分也就越有价值,增益的计算公式如下:
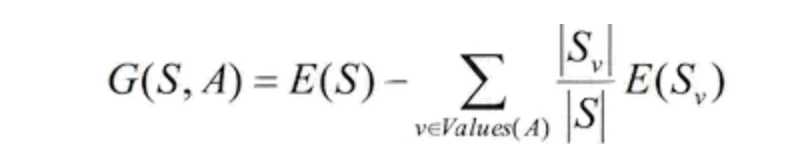
上述公式可以理解为:计算这次划分之后两个子集的熵之和相对划分之前的熵减少了多少,需要注意的是,计算子集的熵之和需要乘上各个子集的权重,权重的计算方法是子集的规模占分割前父集的比重,比如划分前熵为e,划分为子集A和B,大小分别为m和n,熵分别为e1和e2,那么增益就是e - m/(m + n) * e1 - n/(m + n) * e2。
有了上述概念,我们就可以开始开始决策树的训练了,训练过程分为:
选取特征,分割样本集
计算增益,如果增益够大,将分割后的样本集作为决策树的子节点,否则停止分割
递归执行上两步
上述步骤是依照ID3的算法思想(依据信息增益进行特征选取和分裂),除此之外还有C4.5以及CART等决策树算法。
class DecisionTree(object):
def fit(self, X, y):
# 依据输入样本生成决策树
self.root = self._build_tree(X, y)
def _build_tree(self, X, y, current_depth=0):
#1. 选取最佳分割特征,生成左右节点
#2. 针对左右节点递归生成子树
def predict_value(self, x, tree=None):
# 将输入样本传入决策树中,自顶向下进行判定
# 到达叶子节点即为预测值
在上述代码中,实现决策树的关键是递归构造子树的过程,为了实现这个过程,我们需要做好三件事:分别是节点的定义,最佳分割特征的选择,递归生成子树。
作者:ZPPenny
链接:http://www.jianshu.com/p/c4d0837e9439
來源:简书
决策树是一种简单常用的分类器,通过训练好的决策树可以实现对未知的数据进行高效分类。
决策树模型具有较好的可读性和描述性,有助于辅助人工分析;
决策树的分类效率高,一次构建后可以反复使用,而且每一次预测的计算次数不超过决策树的深度。
决策树也有其缺点:
对于连续的特征,比较难以处理。
对于多分类问题,计算量和准确率都不理想。
在实际应用中,由于其最底层叶子节点是通过父节点中的单一规则生成的,所以通过手动修改样本特征比较容易欺骗分类器,比如在拦击邮件识别系统中,用户可能通过修改某一个关键特征,就可以骗过垃圾邮件识别系统。从实现上来讲,由于树的生成采用的是递归,随着样本规模的增大,计算量以及内存消耗会变得越来越大。
过拟合也是决策树面临的一个问题,完全训练的决策树(未进行剪纸,未限制Gain的阈值)能够100%准确地预测训练样本,因为其是对训练样本的完全拟合,但是,对与训练样本以外的样本,其预测效果可能会不理想,这就是过拟合。
解决决策树的过拟合,除了上文说到的通过设置Gain的阈值作为停止条件之外,通常还需要对决策树进行剪枝,常用的剪枝策略有
1.Pessimistic Error Pruning:悲观错误剪枝
2.Minimum Error Pruning:最小误差剪枝
3.Cost-Complexity Pruning:代价复杂剪枝
4. Error-Based Pruning:基于错误的剪枝,即对每一个节点,都用一组测试数据集进行测试,如果分裂之后,能够降低错误率,再继续分裂为两棵子树,否则直接作为叶子节点。
5. Critical Value Pruning:关键值剪枝,这就是上文中提到的设置Gain的阈值作为停止条件。
以最简单的方式展示了ID3决策树的实现方式,如果想要了解不同类型的决策树的差别,可以参考这个链接。
另外,关于各种机器学习算法的实现,强烈推荐参考Github仓库ML-From-Scratch,下载代码之后,通过pip install -r requirements.txt安装依赖库即可运行代码。
标签:规则 cal 树模型 实验 连续 树形结构 diff 重要 机器学习算法
原文地址:http://www.cnblogs.com/wade-luffy/p/7718701.html