标签:ima clu void int get 自己 bsp ace har
给定一个带权值的无向图,要求权值之和最小的生成树,常用的算法有Kruskal算法和Prim算法。这篇文章先介绍Kruskal算法。
Kruskal算法的基本思想:先将所有边按权值从小到大排序,然后按顺序选取每条边,假如一条边的两个端点不在同一个集合中,就将这两个端点合并到同一个集合中;假如两个端点在同一个集合中,说明这两个端点已经连通了,就将当前这条边舍弃掉;当所有顶点都在同一个集合时,说明最小生成树已经形成。(写代码的时候会将所有边遍历一遍)
来看一个例子:
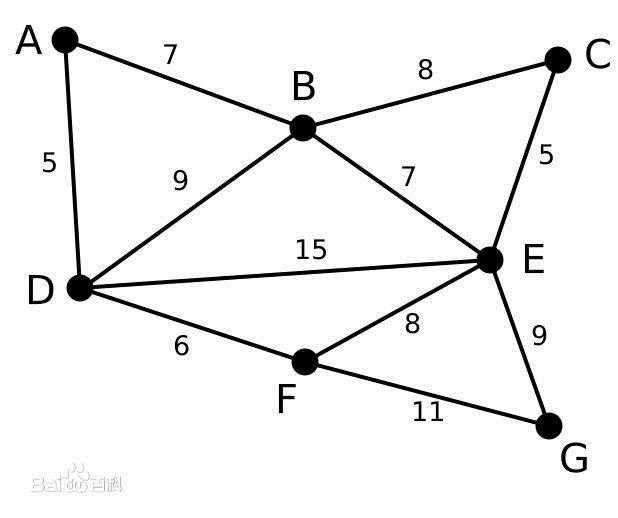
步骤:
(1)先根据权值把边排序:
AD 5
CE 5
DF 6
AB 7
BE 7
BC 8
EF 8
BD 9
EG 9
FG 11
(2)
选择AD这条边,将A、D加到同一个集合1中
选择CE这条边,将C、E加到同一个集合2中(不同于AD的集合)
选择DF这条边,由于D已经在集合1中,因此将F加入到集合1中,集合变为A、D、F
选择AB这条边,同理,集合1变为A、B、D、F
选择BE这条边,由于B在集合1中,E在集合2中,因此将两个集合合并,形成一个新的集合ABCDEF
由于E、F已经在同一集合中,舍弃掉BC这条边;同理舍弃掉EF、BD
选择EG这条边,此时所有元素都已经在同一集合中,最小生成树形成
象征性地舍弃掉FG这条边
实现代码如下:
#include <iostream> #include <cstring> #define MaxSize 20 using namespace std; struct Edge{ int begin; int end; int weight; }; struct Graph{ char ver[MaxSize + 1]; int edg[MaxSize][MaxSize]; }; void CreateGraph(Graph *g) { int VertexNum; char Ver; int i = 0; cout << "输入图的顶点:" << endl; while ((Ver = getchar()) != ‘\n‘) { g->ver[i] = Ver; i++; } g->ver[i] = ‘\0‘; VertexNum = strlen(g->ver); cout << "输入相应的邻接矩阵" << endl; for (int i = 0; i < VertexNum; i++) { for (int j = 0; j < VertexNum; j++) { cin >> g->edg[i][j]; //输入0则为没有边相连啊 } } } void PrintGraph(Graph g) { int VertexNum = strlen(g.ver); cout << "图的顶点为:" << endl; for (int i = 0; i < VertexNum; i++) { cout << g.ver[i] << " "; } cout << endl; cout << "图的邻接矩阵为:" << endl; for (int i = 0; i < VertexNum; i++) { for (int j = 0; j < VertexNum; j++) { cout << g.edg[i][j] << " "; } cout << endl; } } int getVerNum(Graph g) { return strlen(g.ver); } int getEdgeNum(Graph g) { int res = 0; int VertexNum = getVerNum(g); for (int i = 0; i < VertexNum; i++) { //邻接矩阵对称,计算上三角元素和即可 for (int j = i + 1 /*假设没有自己指向自己的*/; j < VertexNum; j++) { if (g.edg[i][j] != 0) res++; } } return res; } Edge *CreateEdges(Graph g) { int k = 0; int EdgeNum = getEdgeNum(g); int VertexNum = getVerNum(g); Edge * p = new Edge[EdgeNum]; for (int i = 0; i < VertexNum; i++) { for (int j = i; j < VertexNum; j++) { if (g.edg[i][j] != 0) { p[k].begin = i; p[k].end = j; p[k].weight = g.edg[i][j]; k++; } } } for (int i = 0; i < EdgeNum - 1; i++) { Edge minWeightEdge = p[i]; for (int j = i + 1; j < EdgeNum; j++) { if (minWeightEdge.weight > p[j].weight) { Edge temp = minWeightEdge; minWeightEdge = p[j]; p[j] = temp; } } p[i] = minWeightEdge; } return p; } void Kruskal(Graph g) { int VertexNum = getVerNum(g); int EdgeNum = getEdgeNum(g); Edge *p = CreateEdges(g); int *index = new int[VertexNum]; //index数组,其元素为连通分量的编号,index[i]==index[j]表示编号为i和j的顶点在同一连通分量中 int *MSTEdge = new int[VertexNum - 1]; //用来存储已确定的最小生成树的**边的编号**,共VertexNum-1条边 int k = 0; int WeightSum = 0; int IndexBegin, IndexEnd; for (int i = 0; i < VertexNum; i++) { index[i] = -1; //初始化所有index为-1 } for (int i = 0; i < VertexNum - 1; i++) { for (int j = 0; j < EdgeNum; j++) { if ( !(index[p[j].begin] >= 0 && index[p[j].end] >= 0 && index[p[j].begin] == index[p[j].end] /*若成立表明p[j].begin和p[j].end已在同一连通块中(且可相互到达,废话)*/) ) { MSTEdge[i] = j; if (index[p[j].begin] == -1 && index[p[j].end] == -1) { index[p[j].begin] = index[p[j].end] = i; } else if (index[p[j].begin] == -1 && index[p[j].end] >= 0) { index[p[j].begin] = i; IndexEnd = index[p[j].end]; for (int n = 0; n < VertexNum; n++) { if (index[n] == IndexEnd) { index[n] == i; } } } else if (index[p[j].begin] >= 0 && index[p[j].end] == -1) { index[p[j].end] = i; IndexBegin = index[p[j].begin]; /*将连通分量合并(或者说将没加入连通分量的顶点加进去,然后将原来连通分量的值改了)*/ for (int n = 0; n < VertexNum; n++) { if (index[n] == IndexBegin) { index[n] == i; } } } else { IndexBegin = index[p[j].begin]; IndexEnd = index[p[j].end]; for (int n = 0; n < VertexNum; n++) { if (index[n] == IndexBegin || index[n] == IndexEnd) { index[n] = i; } } } break; } } } cout << "MST的边为:" << endl; for (int i = 0; i < VertexNum - 1; i++) { cout << g.ver[p[MSTEdge[i]].begin] << "--" << g.ver[p[MSTEdge[i]].end] << endl; WeightSum += p[MSTEdge[i]].weight; } cout << "MST的权值为:" << WeightSum << endl; }
标签:ima clu void int get 自己 bsp ace har
原文地址:http://www.cnblogs.com/fengziwei/p/7738389.html