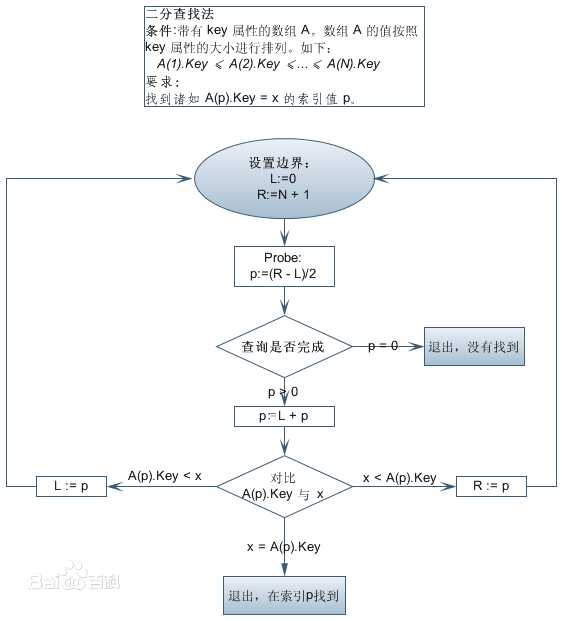
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其
缺点是要求待查表为有序表,且插入删除困难。因此,折半查找方法适用于不经常变动而查找频繁的有序列表。首先,假设表中元素是按升序排列,将表中间位置记录的
关键字与查找关键字比较,如果两者相等,则查找成功;否则利用中间位置
记录将表分成前、后两个子表,如果中间位置记录的关键字大于查找关键字,则进一步查找前一子表,否则进一步查找后一子表。重复以上过程,直到找到满足条件的
记录,使查找成功,或直到子表不存在为止,此时查找不成功。
- 思想
- 二分查找是每次查找的时候从中间开始查找,前提是这个要查找的数组或者列表必须是按顺序排好的。比如从1-100的顺序排好的数,我想随意想一个数字,你来猜,当你猜的数字比我的数大,我会说`大了`,你就要再往`小`的一边开始猜;当你猜的数字比我的小,我会说`小了`,你就要往`大`的一边猜。所以,当你每次从中间开始猜的时候,猜的次数最少。
-总结:
二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;如果x<a[n/2],则只要在数组a的左半部分继续搜索x,如果x>a[n/2],则只要在数组a的右半部搜索x.
时间复杂度无非就是while循环的次数!
总共有n个元素,
渐渐跟下去就是n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数
由于你n/2^k取整后>=1
即令n/2^k=1
可得k=log2n,(是以2为底,n的对数)
所以时间复杂度可以表示O(h)=O(log2n)
-算法要求
-
必须采用顺序存储结构。
2.必须按关键字大小有序排列。
- 运行时间
- 当你从1开始顺序猜时,最多需要猜100次,即`O(n)` 线性时间;
- 当用二分法猜时,每次猜测排除一半即除以2,除不开是向上取整直到剩余一个数时 是你可能猜的最多的次数。`100/2/2/2/2/2/2/2=1 ` 除2的次数为你猜的次数。这个数为以2为低100的对数:`㏒?10` 对数时间;
-它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。它的基本思想是,将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法终止。如 果x<a[n/2],则我们只要在
数组a的左半部继续搜索x(这里假设数组元素呈升序排列)。如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。
- 算法代码 (python3)
```python
def binary_search(list , item):
low = 0
high = len(list) - 1
while low <= high:
mid = (low + high) // 2
guess = list[mid]
if guess == item:
return mid
if guess < item:
low = mid + 1
else:
high = mid -1
return None
myList = [1,4,6,8,9]
print(binary_search(myList,10))
print(binary_search(myList,6))
```
