标签:多点 输入格式 没有 遇到 start ace ++i 表示 show
前两天刚刚做完2014年noipD1T3飞扬的小鸟
其实这道题本身并不是一道很难的DP
状态容易想到,转移也容易想到
但是出于我的基础较差,还是出了较大的偏差
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
游戏界面是一个长为n ,高为 m 的二维平面,其中有k 个管道(忽略管道的宽度)。
小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
如果不点击屏幕,小鸟就会下降一定高度Y 。小鸟位于横坐标方向不同位置时,上升的高度X 和下降的高度Y 可能互不相同。
现在,请你判断是否可以完成游戏。如果可以 ,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
输入格式:
第1 行有3 个整数n ,m ,k ,分别表示游戏界面的长度,高度和水管的数量,每两个
整数之间用一个空格隔开;
接下来的n 行,每行2 个用一个空格隔开的整数X 和Y ,依次表示在横坐标位置0 ~n- 1
上玩家点击屏幕后,小鸟在下一位置上升的高度X ,以及在这个位置上玩家不点击屏幕时,
小鸟在下一位置下降的高度Y 。
接下来k 行,每行3 个整数P ,L ,H ,每两个整数之间用一个空格隔开。每行表示一
个管道,其中P 表示管道的横坐标,L 表示此管道缝隙的下边沿高度为L ,H 表示管道缝隙
上边沿的高度(输入数据保证P 各不相同,但不保证按照大小顺序给出)。
输出格式:
共两行。
第一行,包含一个整数,如果可以成功完成游戏,则输出1 ,否则输出0 。
第二行,包含一个整数,如果第一行为1 ,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
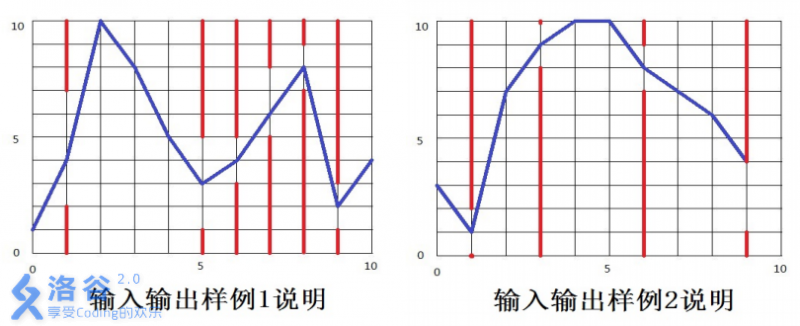
【数据范围】
对于30% 的数据:5 ≤ n ≤ 10,5 ≤ m ≤ 10,k = 0 ,保证存在一组最优解使得同一单位时间最多点击屏幕3 次;
对于50% 的数据:5 ≤ n ≤ 2 0 ,5 ≤ m ≤ 10,保证存在一组最优解使得同一单位时间最多点击屏幕3 次;
对于70% 的数据:5 ≤ n ≤ 1000,5 ≤ m ≤ 1 0 0 ;
对于100%的数据:5 ≤ n ≤ 100 0 0 ,5 ≤ m ≤ 1 0 00,0 ≤ k < n ,0<X < m ,0<Y <m,0<P <n,0 ≤ L < H ≤ m ,L +1< H 。
一开始读完题目,就非常迅速的想到了DP,于是上手就开始打了,
粗粗的列了列式子,并没有算复杂度,于是一开始复杂度接近 O(n*m*m)
第一遍打完,调过了样例,又测了几组发现都非常正确,于是果断交

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 const int N=10010; 8 int up[N],dw[N],sum[N],d[N],u[N],f[N][1010]; 9 int n,m,k,x,y,z; 10 int main(){ 11 scanf("%d%d%d",&n,&m,&k); 12 for (int i=1;i<=n;++i) scanf("%d%d",&up[i],&dw[i]); 13 for (int i=1;i<=k;++i) 14 scanf("%d%d%d",&x,&y,&z),u[x]=y,d[x]=z; 15 for (int i=1;i<=n;++i) sum[i]=sum[i-1]+(d[i]>0); 16 for (int i=0;i<=n;++i) for (int j=0;j<=m;++j) f[i][j]=1e9; 17 for (int i=0;i<=m;++i) f[0][i]=0; 18 for (int i=1;i<=n;++i) 19 for (int j=1;j<=m;++j) if (f[i-1][j]<1e9){ 20 if (j>dw[i]) 21 if (u[i]||d[i]){ 22 if (j-dw[i]>u[i]&&j-dw[i]<d[i]) f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 23 } else f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 24 25 int lim=(m-j)/up[i]; 26 if ((m-j)%up[i]==0) lim++; 27 for (int k=1;k<=lim;++k){ 28 int he=j+k*up[i]; if (he>m) he=m; 29 if (u[i]||d[i]){ 30 if (he>u[i]&&he<d[i]) f[i][he]=min(f[i][he],f[i-1][j]+k); 31 } else f[i][he]=min(f[i][he],f[i-1][j]+k); 32 } 33 } 34 int ans=1e9; 35 // for (int i=1;i<=n;++i) 36 // for (int j=1;j<=m;++j) if (f[i][j]!=1e9) printf("f[%d][%d]=%d\n",i,j,f[i][j]); 37 for (int i=1;i<=m;++i) 38 ans=min(ans,f[n][i]); 39 if (ans<1e9) printf("1\n%d",ans); else 40 for (int i=1;i<=n;++i){ 41 bool flag=1; 42 for (int j=1;j<=m;++j) 43 if (f[i][j]<1e9){flag=0; break;} 44 if (flag){printf("0\n%d",sum[i-1]); return 0;} 45 } 46 47 }
结果发现题意理解不够清楚,因为它在m高度的时候也可以继续跳,只是高度不变,于是改了一发再交

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 const int N=10010; 8 int up[N],dw[N],sum[N],d[N],u[N],f[N][1010]; 9 int n,m,k,x,y,z; 10 int main(){ 11 scanf("%d%d%d",&n,&m,&k); 12 for (int i=1;i<=n;++i) scanf("%d%d",&up[i],&dw[i]); 13 for (int i=1;i<=k;++i) 14 scanf("%d%d%d",&x,&y,&z),u[x]=y,d[x]=z; 15 for (int i=1;i<=n;++i) sum[i]=sum[i-1]+(d[i]>0); 16 for (int i=0;i<=n;++i) for (int j=0;j<=m;++j) f[i][j]=1e9; 17 for (int i=1;i<=m;++i) f[0][i]=0; 18 for (int i=1;i<=n;++i) 19 for (int j=1;j<=m;++j) if (f[i-1][j]<1e9){ 20 if (j>dw[i]) 21 if (u[i]||d[i]){ 22 if (j-dw[i]>u[i]&&j-dw[i]<d[i]) f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 23 } else f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 24 25 int lim=(m-j)/up[i]; 26 if ((m-j)%up[i]!=0||(m-j==0)) lim++; 27 for (int k=1;k<=lim;++k){ 28 int he=j+k*up[i]; if (he>m) he=m; 29 if (u[i]||d[i]){ 30 if (he>u[i]&&he<d[i]) f[i][he]=min(f[i][he],f[i-1][j]+k); 31 } else f[i][he]=min(f[i][he],f[i-1][j]+k); 32 } 33 } 34 int ans=1e9; 35 // for (int i=1;i<=n;++i) 36 // for (int j=1;j<=m;++j) if (f[i][j]!=1e9) printf("f[%d][%d]=%d\n",i,j,f[i][j]); 37 for (int i=1;i<=m;++i) 38 ans=min(ans,f[n][i]); 39 if (ans<1e9) printf("1\n%d",ans); else 40 for (int i=1;i<=n;++i){ 41 bool flag=1; 42 for (int j=1;j<=m;++j) 43 if (f[i][j]<1e9){flag=0; break;} 44 if (flag){printf("0\n%d",sum[i-1]); return 0;} 45 } 46 47 }
T75 现在突然意识到自己的DP复杂度根本不对
贴了快读,加了register,再交

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 const int N=10010; 7 int up[N],dw[N],sum[N],d[N],u[N],f[N][1010]; 8 int n,m,k,x,y,z; 9 template<class T> 10 inline void read(T &x) { 11 bool Finish_read=0;x=0;int f=1;char ch=getchar(); 12 while(!isdigit(ch)){if(ch==‘-‘)f=-1;if(ch==EOF) return;ch=getchar();} 13 while(isdigit(ch))x=x*10+ch-‘0‘,ch=getchar(); 14 x*=f;Finish_read=1; 15 } 16 template<class T> 17 inline void print(T x) { 18 if(x/10!=0) print(x/10); 19 putchar(x%10+‘0‘); 20 } 21 template<class T> 22 inline void writeln(T x) { 23 if(x<0) putchar(‘-‘); 24 print(x); putchar(‘\n‘); 25 } 26 inline int min(int x,int y){return x<y?x:y;} 27 int main(){ 28 read(n); read(m); read(k); 29 for (register int i=1;i<=n;++i) read(up[i]),read(dw[i]); 30 for (register short i=1;i<=k;++i) 31 read(x),read(y),read(z),u[x]=y,d[x]=z; 32 for (register int i=1;i<=n;++i) sum[i]=sum[i-1]+(d[i]>0); 33 for (register int i=0;i<=n;++i) for (short j=0;j<=m;++j) f[i][j]=1e9; 34 for (register short i=1;i<=m;++i) f[0][i]=0; 35 for (register int i=1;i<=n;++i) 36 for (register short j=1;j<=m;++j) if (f[i-1][j]<1e9){ 37 if (j>dw[i]) 38 if (d[i]>0){ 39 if (j-dw[i]>u[i]&&j-dw[i]<d[i]) f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 40 } else f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 41 42 int lim=(m-j)/up[i]; 43 if ((m-j)%up[i]!=0||(m-j==0)) lim++; 44 for (register short k=1;k<=lim;++k){ 45 int he=j+k*up[i]; if (he>m) he=m; 46 if (d[i]>0){ 47 if (he>u[i]&&he<d[i]) f[i][he]=min(f[i][he],f[i-1][j]+k); 48 } else f[i][he]=min(f[i][he],f[i-1][j]+k); 49 } 50 } 51 int ans=1e9; 52 for (register short i=1;i<=m;++i) 53 ans=min(ans,f[n][i]); 54 if (ans<1e9) printf("1\n%d",ans); else 55 for (register int i=1;i<=n;++i){ 56 bool flag=1; 57 for (register short j=1;j<=m;++j) 58 if (f[i][j]<1e9){flag=0; break;} 59 if (flag){printf("0\n%d",sum[i-1]); return 0;} 60 } 61 62 }
好像多了5分,但并没什么用
到了晚上,在想这道题,大力加了一发剪枝,剪掉了一些不必要DP的情况

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 const short N=10010; 7 int up[N],dw[N],sum[N],d[N],u[N],f[N][1010]; 8 int n,m,k,x,y,z,ans=0; 9 template<class T> 10 inline void read(T &x) { 11 bool Finish_read=0;x=0;int f=1;char ch=getchar(); 12 while(!isdigit(ch)){if(ch==‘-‘)f=-1;if(ch==EOF) return;ch=getchar();} 13 while(isdigit(ch))x=x*10+ch-‘0‘,ch=getchar(); 14 x*=f;Finish_read=1; 15 } 16 template<class T> 17 inline void print(T x) { 18 if(x/10!=0) print(x/10); 19 putchar(x%10+‘0‘); 20 } 21 template<class T> 22 inline void writeln(T x) { 23 if(x<0) putchar(‘-‘); 24 print(x); putchar(‘\n‘); 25 } 26 inline int min(int x,int y){return x<y?x:y;} 27 bool check(int x){ 28 for(int i=u[x]+1;i<=d[x]-1;i++) 29 if (f[x][i]<1e9) return 1; 30 return 0; 31 } 32 int main(){ 33 read(n); read(m); read(k); 34 for (register int i=1;i<=n;++i) read(up[i]),read(dw[i]); 35 for (register short i=1;i<=k;++i) 36 read(x),read(y),read(z), 37 u[x]=y,d[x]=z; 38 for (register int i=1;i<=n;++i) 39 sum[i]=sum[i-1]+(d[i]>0); 40 for (register short i=0;i<=n;++i) 41 for (short j=0;j<=m;++j) f[i][j]=1e9; 42 for (register short i=1;i<=m;++i) f[0][i]=0; 43 44 // 45 for (register int i=1;i<=n;++i){ 46 short l=1,r=m; 47 if (d[i-1]>0) 48 l=u[i-1]+1,r=d[i-1]-1,ans++; 49 for (register short j=r;j>=l;--j) if (f[i-1][j]<1e9){ 50 if (j>dw[i]) 51 f[i][j-dw[i]]=min(f[i][j-dw[i]],f[i-1][j]); 52 for (register short k=1;k<=m/up[i]+1;++k){ 53 int he=j+k*up[i]; 54 if (d[i]>0){ 55 if (he>=d[i]) break; 56 if (he<=u[i]) continue; 57 } 58 if (he<m){ 59 if (f[i-1][j]+k>f[i][he]) break; 60 f[i][he]=f[i-1][j]+k; 61 } else { 62 f[i][m]=min(f[i-1][j]+k,f[i][m]); break; 63 } 64 } 65 } 66 if (d[i]&&!check(i)) break; 67 } 68 if (ans<k){ 69 printf("0\n%d",ans); return 0; 70 } 71 int l=1,r=m; ans=1e9; 72 if (d[n]>0) l=u[n]+1,r=d[n]-1; 73 for (int i=l;i<=r;++i) ans=min(ans,f[n][i]); 74 printf("1\n%d",ans); 75 return 0; 76 }
然后就跑的飞快了QAQ
当然以上的过程我已经将他简化,事实上我还交了很多很多发(本人比较菜没办法)
(1)比赛时候做题,不要慌张,看完题目不要马上上手,仔细读完所有题目给定的条件
(2)如遇到这种DP题,要清楚的算清复杂度,如会T,需要大力加剪枝,或重新思考
(3)积极打暴力,如有时间一定要对拍
标签:多点 输入格式 没有 遇到 start ace ++i 表示 show
原文地址:http://www.cnblogs.com/logic-yzf/p/7749931.html