标签:除了 线性模型 max alpha alt off logo 转换 epo
用于分类:k近邻,朴素贝叶斯,决策树,规则学习,神经网络,支持向量机
用于数值预测:线性回归,回归树,模型树,神经网络,支持向量机
用于模式识别(数据之间联系的紧密性):关联规则
用于聚类:k均值聚类
llibrary(class)
library(gmodels)
#prepare data
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
iris_z <- as.data.frame(scale(iris_rand[,-5])) #z score normalize
train <- iris_z[1:105,]
test <- iris_z[106:150,]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#kNN
pred <- knn(train,test,train.label,k=10)
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
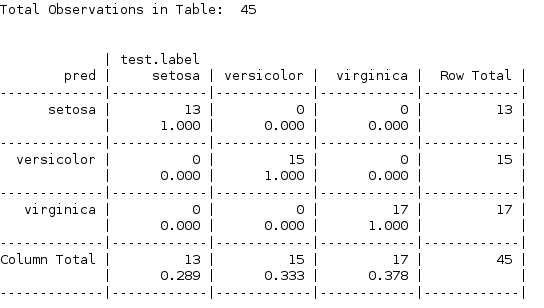
??这个结果显示kNN对测试数据全部预测正确
library(e1071)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,-5]
test <- iris_rand[106:150,-5]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#tranform numerical variable to classified variable
conver_counts <- function(x){
q <- quantile(x)
sect1 <- which(q[1] <= x & x<= q[2])
sect2 <- which(q[2 ]< x & x <= q[3])
sect3 <- which(q[3]< x & x <= q[4])
sect4 <- which(q[4]< x & x <= q[5])
x[sect1] <- 1
x[sect2] <- 2
x[sect3] <- 3
x[sect4] <- 4
return(x)
}
train <- apply(train,2,conver_counts)
#naiveBayes
m <- naiveBayes(train,train.label,laplace=1)
pred <- predict(m,test,type="class")
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
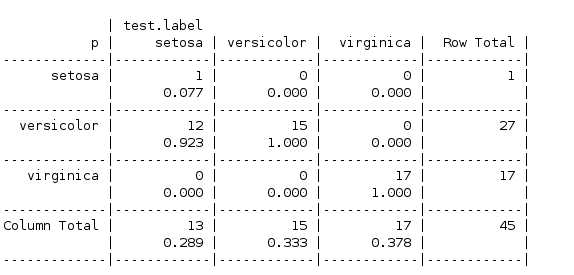
可见对第一类(setosa)分类上预测错误率很高,这可能反映了朴素贝叶斯算法的缺点,对于处理大量数值特征数据集时并不理想
library(C50)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,-5]
test <- iris_rand[106:150,-5]
train.label <- iris_rand[1:105,5]
test.label <- iris_rand[106:150,5]
#C50
m <- C5.0(train,train.label,trials = 10)
pred <- predict(m,test,type="class")
#comfusion matrix
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)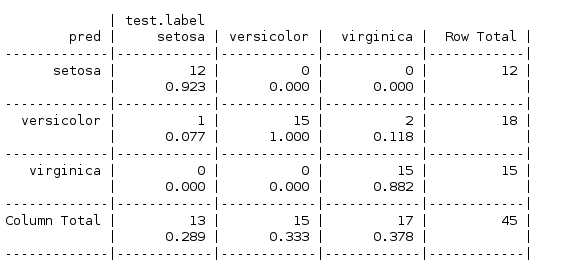
library(RWeka)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,]
test <- iris_rand[106:150,-5]
test.label <- iris_rand[106:150,5]
m <- OneR(Species ~ .,data=train)
pred <- predict(m,test)
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)
查看生成的规则,按照Petal的宽度,分成三类,正确分类了105个里面的101个
对于测试数据的混合矩阵如下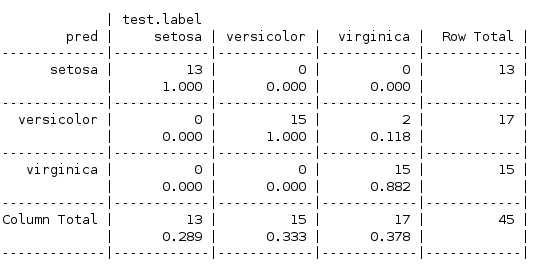
可见只使用了一个规则也能,也做到了不错的效果
??对于复杂的任务,只考虑单个规则可能过于简单,考虑多个因素的更复杂的规则学习算法可能会有用,但也可能因此会变得更加难以理解。早期的规则学习算法速度慢,并且对于噪声数据往往不准确,后来出现增量减少误差修剪算法(IREP),使用了生成复杂规则的预剪枝和后剪枝方法的组合,并在案例从全部数据集分离之前进行修剪。虽然这提高了性能,但是还是决策树表现的更好。直到1995年出现了重复增量修剪算法(RIPPER),它对IREP算法进行改进后再生成规则,它的性能与决策树相当,甚至超过决策树。
library(RWeka)
library(gmodels)
set.seed(12345) #set random seed in order to repeat the result
iris_rand <- iris[order(runif(150)),]
train <- iris_rand[1:105,]
test <- iris_rand[106:150,-5]
test.label <- iris_rand[106:150,5]
m <- JRip(Species ~ .,data=train)
pred <- predict(m,test)
CrossTable(pred,test.label,prop.r = F,prop.t = F,prop.chisq = F)

这次使用了三个规则,(Petal.Width >= 1.8为virginica ,Petal.Length >= 3为versicolor,其它为setosa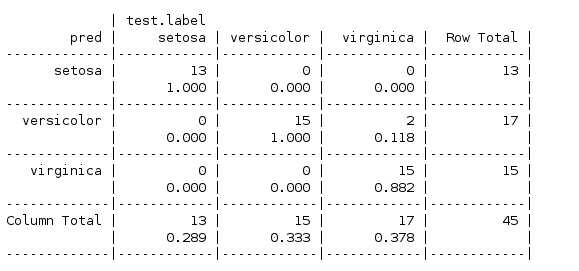
可见虽然增加了规则但是并没有提高模型的性能
??回归主要关注一个唯一的因变量(需要预测的值)和一个或多个数值型自变量之间的关系。
??x: 输入矩阵,每列表示变量(特征),每行表示一个观察向量,也支持输入稀疏矩阵(Matrix中的稀疏矩阵类);
??y: 反应变量,对于gaussian或者poisson分布族,是相应的量;对于binomial分布族,要求是两水平的因子,或者两列的矩阵,第一列是计数或者是比例,第二列是靶向分类;对于因子来说,最后的水平是按照字母表排序的分类;对于multinomial分布族,能有超过两水平的因子。无论binomial或者是multinomial,如果y是向量的话,会强制转化为因子。对于cox分布族,y要求是两列,分别是time和status,后者是二进制变两,1表示死亡,0表示截尾,survival包带的Surv()函数可以产生这样的矩阵。对于mgaussian分布族,y是量化的反应变量的矩阵;
??family: 反应类型,参数family规定了回归模型的类型:family="gaussian"适用于一维连续因变量(univariate)family="mgaussian",适用于多维连续因变量(multivariate),family="poisson"适用于非负次数因变量(count),family="binomial"适用于二元离散因变量(binary),family="multinomial"适用于多元离散因变量(category)
??weights: 权重,观察的权重。如果反应变量是比例矩阵的话,权重是总计数;默认每个观察权重都是1;
??offset: 包含在线性预测中的和观察向量同样长度的向量,在poisson分布族中使用(比如log后的暴露时间),或者是对于已经拟合的模型的重新定义(将旧模型的因变量作为向量放入offset中)。默认是NULL,如果提供了值,该值也必须提供给predict函数;
??alpha: 弹性网络混合参数,0 <= a <=1,惩罚定义为(1-α)/2||β||_2^2+α||β||_1.其中alpha等于1是lasso惩罚,alpha等于0是ridge(岭回归)的惩罚;
??nlambda:lambda值个数;拟合出n个系数不同的模型
??lambda.min.ratio:lambda的最小值,lambda.max的比例形式,比如全部系数都是0的时候的最小值。默认值依赖于观察的个数和特征的个数,如果观察个数大于特征个数,默认值是0.0001,接近0,如果观察个数小于特征个数,默认值是0.01。在观察值个数小于特征个数的情况下,非常小的lambda.min.ratio会导致过拟合,在binominal和multinomial分布族性,这个值未定义,如果解释变异百分比总是1的话程序会自动退出;
??lambda:用户提供的lambda序列。一个典型的用法基于nlambada和lambda.min.ratio来计算自身lambda序列。如果提供lambda序列,提供的lambda序列会覆盖这个。需谨慎使用,不要提供单个值给lambda(对于CV步骤后的预测,应使用predict()函数替代)。glmnet依赖于缓慢开始,并且它用于拟合全路径比计算单个拟合更快;
??standardize:对于x变量是否标准化的逻辑标志,倾向于拟合模型序列。 系数总是在原有规模返回,默认standardize=TRUE。如果变量已经是同一单位,你可能并不能得到想要的标准化结果。
??intercept:是否拟合截距,默认TRUE,或者设置为0(FALSE)
??thresh:坐标下降的收敛域值,每个内部坐标下降一直进行循环,直到系数更新后的最大改变值比thresh值乘以默认变异要小,默认thresh为1E-7;
??dfmax:在模型中的最大变量数,对于大量的变量数的模型但我们只需要部分变量时可以起到作用;
??pmax:限制非零变量的最大数目;
??exclude:要从模型中排除的变量的索引,等同于一个无限的惩罚因子;
??penalty.factor:惩罚因子,分开的惩罚因子能够应用到每一个系数。这是一个数字,乘以lambda来允许不同的收缩。对于一些变量来说可以是0,意味着无收缩,默认对全部变量是1,对于列在exlude里面的变量是无限大。注意:惩罚因子是内部对nvars(n个变量)的和进行重新调整,并且lambda序列将会影响这个改变;
??lower.limits:对于每个系数的更低限制的向量,默认是无穷小。向量的每个值须非正值。也可以以单个值呈现(将会重复),或者是(nvars长度);
??upper.limit:对于每个系数的更高限制的向量,默认是无穷大;
??maxit:所有lambda值的数据最大传递数;
??type.gaussian:支持高斯分布族的两种算法类型,默认nvar < 500使用"covariance“,并且保留所有内部计算的结果。这种方式比"naive"快,"naive"通过对nobs(n个观察)进行循环,每次内部计算一个结果,对于nvar >> nobs或者nvar > 500的情况下,后者往往更高效;
??type.logistic:如果是"Newton“,会使用准确的hessian矩阵(默认),当用的是"modified.Newton“时,只使用hession矩阵的上界,会更快;
??standardize.response:这个参数时对于"mgaussian“分布族来说的,允许用户标准化应答变量;
??type.multinomial:如果是"grouped",在多项式系数的变量使用分布lasso惩罚,这样能确保它们完全在一起,默认是"ungrouped"。
glmnet返回S3类,"glmnet","*","*"可以是elnet,lognet,multnet,fishnet(poisson),merlnet
??call:产生这个对象的调用;
??a0:截距;
??beta:对于elnet, lognet, fishnet和coxnet模型,返回稀疏矩阵格式的系数矩阵(CsparseMatrix),对于multnet和mgaussian模型,返回列表,包括每一类的矩阵;
??lambda:使用的lambda值的实际序列;当alpha=0时,最大的lambda值并不单单等于0系数(原则上labda等于无穷大),相反使用alpha=0.01的lambda,由此导出lambda值;
??dev.ratio:表示由模型解释的变异的百分比(对于elnet,使用R-sqare)。如果存在权重,变异计算会加入权重,变异定义为2x(loglike_sat-loglike),loglike_sat是饱和模型(每个观察值具有自由参数的模型)的log似然。因此dev.ratio=1-dev/nulldev;越接近1说明模型的表现越好
??nulldev:NULL变异(每个观察值),这个定义为2*(loglike_sat-loglike(Null));NULL模型是指截距模型,除了Cox(0 模型);
??df:对于每个lambda的非零系数的数量。对于multnet这是对于一些类的变量数目;
??dfmat:仅适用于multnet和mrelnet。一个包括每一类的非零向量数目的矩阵;
??dim:系数矩阵的维度;
??nobs:观察的数量;
??npasses:全部lambda值加和的数据的总的通量;
??offset:逻辑变量,显示模型中是否包含偏移;
??jerr:错误标记,用来警告和报错(很大部分用于内部调试验)
??而直接显示的结果有三列,分别是df,%Dev (就是dev.ratio),lambda是每个模型对应的λ值
predict(object,newx,s=NULL,type=c("link","reponse","coefficients","nonzero","class"),exact=FALSE,offset,...)
??coef(object,s=NULL,exact=FALSE)
??object:glmnet返回的对象;
??newx:用来预测的矩阵,也可以是系数矩阵;这个参数不能用于type=c(""coefficents","nonzero");
??s:惩罚参数lambda的值,默认是用来创建模型的全部lambda值;
??type:预测值的类型;"link”类型给"binomial",“multinomial","poisson"或者"cov"模型线性预测的值,对于"gaussian”模型给拟合值。"response"类型,对于"binominal“和"multinomial”给拟合的概率,对于"poisson“,给拟合的均值,对于"cox",给拟合的相对未及;对于"gaussion",response等同于"link“类型。"coefficients"类型对于需求的s值计算系数。注意,对于"binomial”模型来说,结果仅仅对因子应答的第二个水平的类返回。“class"类型仅仅应用于"binomial”和"multinomial“模型,返回最大可能性的分类标签。"nonzero”类型对每个s中的值返回一个列表,其中包含非0参数的索引;
??exact:这个参数仅仅对于用于预测的s(lambda)值不同于原始模型的拟合的值时,这个参数起到作用。如果exact=FALSE(默认),预测函数使用线性解释来对给的s(lambda)值进行预测。这时一个非常接近的结果,只是稍微有点粗糙。如果exact=TRUE,这些不同的s值和拟合对象的lambda值进行sorted和merged,在作出预测之前进行模型的重新拟合。在这种情况下,强烈建议提供原始的数据x=和y=作为额外的命名参数给perdict()或者coef(),predict.glmnet()需要升级模型,并且期望用于创建接近它的数据。尽管不提供这些额外的参数它也会运行的很好,在调用函数中使用嵌套序列很可能会中断。
??offset:如果使用offset参数来拟合,必须提供一个offset参数来作预测。除了类型"coefficients"或者"nonzero“(本文转载自 ywliao )
)
标签:除了 线性模型 max alpha alt off logo 转换 epo
原文地址:http://www.cnblogs.com/Recordedit/p/7753305.html