标签:自然数 序列 col size 排序 输入 问题 次数 实施
算法是特定问题求解步骤的描述
在计算机中表现为指令的有限序列
算法是独立存在的一种解决问题的方法和思想。
对于算法而言,语言并不重要,重要的是思想。

数据结构只是静态的描述了数据元素之间的关系
高效的程序需要在数据结构的基础上设计和选择算法
程序=数据结构+算法
总结:
算法是为了解决实际问题而设计的
数据结构是算法需要处理的问题载体
数据结构与算法相辅相成
输入
算法具有0个或多个输入
输出
算法至少有1个或多个输出
有穷性
算法在有限的步骤之后会自动结束而不会无限循环
确定性
算法中的每一步都有确定的含义,不会出现二义性
可行性
算法的每一步都是可行的
1、事后统计法
比较不同算法对同一组输入数据的运行处理时间
缺陷
为了获得不同算法的运行时间必须编写相应程序
运行时间严重依赖硬件以及运行时的环境因素
算法的测试数据的选取相当困难
事后统计法虽然直观,但是实施困难且缺陷多。
2、事前分析估算
依据统计的方法对算法效率进行估算
影响算法效率的主要因素
算法采用的策略和方法
问题的输入规模
编译器所产生的代码
计算机执行速度
#define _CRT_SECURE_NO_WARNINGS #include <iostream> #include <string> //算法最终编译成具体的计算机指令 //每一个指令,在具体的计算机上运行速度固定 //通过具体的n的步骤,就可以推导出算法的复杂度 long sum1(int n) { long ret = 0; int* array = (int*)malloc(n * sizeof(int)); int i = 0; for(i=0; i<n; i++) { array[i] = i + 1; } for(i=0; i<n; i++) { ret += array[i]; } free(array); return ret; } long sum2(int n) { long ret = 0; int i = 0; for(i=1; i<=n; i++) { ret += i; } return ret; } long sum3(int n) { long ret = 0; if( n > 0 ) { ret = (1 + n) * n / 2; } return ret; } void mytest() { printf("%d\n", sum1(100)); printf("%d\n", sum2(100)); printf("%d\n", sum3(100)); return; } int main() { mytest(); system("pause"); return 0; }
int func(int a[], int len) { int i = 0; int j = 0; int s = 0; for(i=0; i<len; i++) n { for(j=0; j<len; j++) n { s += i*j; //n*n } } return s; } //n*n
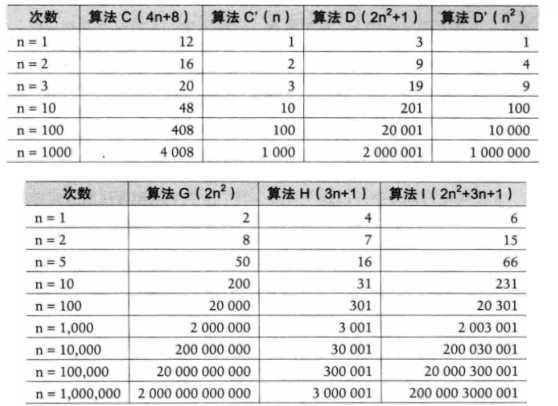
注意1:判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数项可以忽略。
注意2:在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度。
2、大O表示法
算法效率严重依赖于操作(Operation)数量
在判断时首先关注操作数量的最高次项
操作数量的估算可以作为时间复杂度的估算
O(5) = O(1)
O(2n + 1) = O(2n) = O(n)
O(n2+ n + 1) = O(n2)
O(3n3+1) = O(3n3) = O(n3)
常见时间复杂度
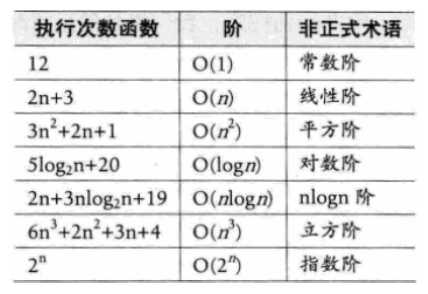
关系
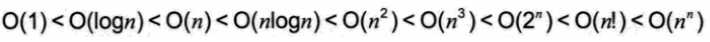
3、算法的空间复杂度
算法的空间复杂度通过计算算法的存储空间实现
S(n) = O(f(n))
其中,n为问题规模,f(n))为在问题规模为n时所占用存储空间的函数
大O表示法同样适用于算法的空间复杂度
当算法执行时所需要的空间是常数时,空间复杂度为O(1)
空间与时间的策略
多数情况下,算法执行时所用的时间更令人关注
如果有必要,可以通过增加空间复杂度来降低时间复杂度
同理,也可以通过增加时间复杂度来降低空间复杂度
#define _CRT_SECURE_NO_WARNINGS #include <stdio.h> #include <stdlib.h> #include <string.h> /* 问题: 在一个由自然数1-1000中某些数字所组成的数组中,每个数字可能出现零次或者多次。 设计一个算法,找出出现次数最多的数字。 */ // 方法1: 排序,然后找出出现次数最多的数字 // 排序,然后找出出现次数最多的数字 // 方法2: 把每个数字出现的次数的中间结果,缓存下来;在缓存的结果中求最大值 void search(int a[], int len) { int sp[1000] = {0}; int i = 0; int max = 0; for (i = 0; i < len; i++) { int index = a[i] - 1; sp[index]++; } for (i = 0; i < 1000; i++) { if (max < sp[i]) { max = sp[i]; } } for (i = 0; i < 1000; i++) { if (max == sp[i]) { printf("%d\n", i + 1); } } } void mytest() { int array[] = {1, 1, 3, 4, 5, 6, 6, 6, 2, 3}; search(array, sizeof(array)/sizeof(array[0])); return; } int main() { mytest(); system("pause"); return 0; }
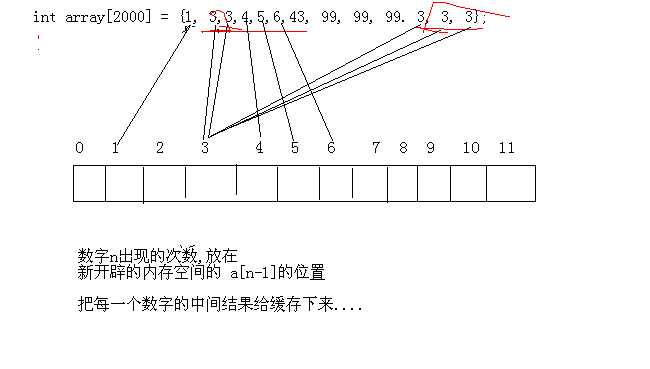
标签:自然数 序列 col size 排序 输入 问题 次数 实施
原文地址:http://www.cnblogs.com/lsgxeva/p/7794280.html