堆排序HeapSort

标签：vector   img   htc   大于等于   规律   数据结构堆   image   循环   没有   

堆排序，顾名思义，是采用数据结构堆来进行排序的一种排序算法。

研究没有规律的堆，没有任何意义。特殊的堆有最大堆（父节点值大于等于左右字节点值），最小堆（父节点值小于等于子节点值）。一般采用最大堆来进行排序，图1为最大堆来表示一维数组。

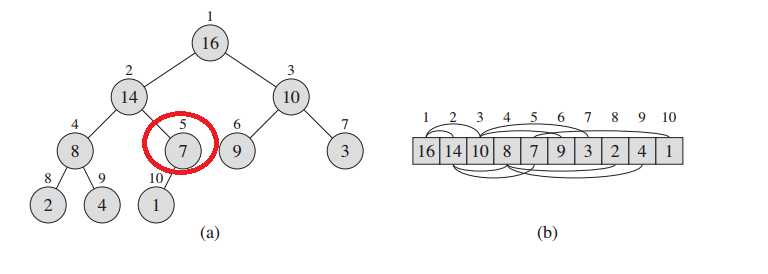
图1 最大堆表示一维数组

2叉树堆的几点特性

1、 最后父节点索引值

不妨设堆的总元素个数为N；最后一个父节点的索引值Index = N/2 ；可以写几个简单的堆进行数学归纳。图1中的最后一个父节点5 = 10 /2 ；

这个特性主要是在采用自底向上构建堆的时候，循环起始值。

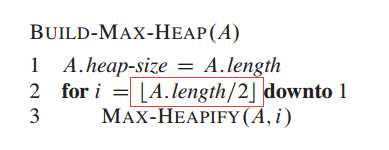
2、父节点与子节点索引值关系

LeftIndex = parent * 2；

RightIndex = parent * 2 + 1;

对于任意一个节点K，其父节点为K/2，其左子节点为2K，右子节点为2K+1。

Max-Heapify（保持最大堆属性）

散乱排布的堆对算法的实现非常不友好，没有意义。因此，在随机数据输入时，需要对数据按照最大堆的属性进行一个初始排序。对一个父节点数据的max-heapify形象的推导直接采用算法导论的图，如图2。节点2的数据显然不符合最大堆的数据定义（父节点值不小于子节点值），因此把MAX(parent，left，right)替换到父节点，父节点的数据替换 到子节点中。对于替换的子节点4，仍然需要判断其是否满足最大堆数据定义，一直递归到满足定义。

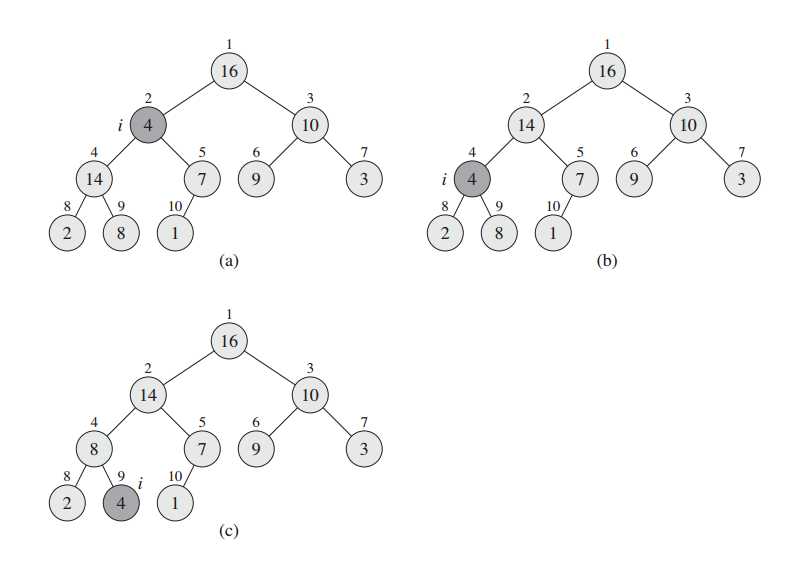
图2 max-heapify原理

构建最大堆

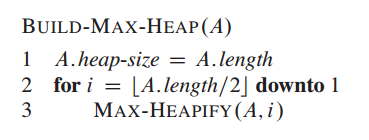
对所有的父节点都进行max-heapify操作，自底向上从最后父节点一直循环到根节点，很巧妙。采用自底向上能够保证遍历过的数据始终是保持最大堆属性的，max-heapify操作始终是求当前父节点下所有子节点的最大值。

那自顶向下会怎样呢？

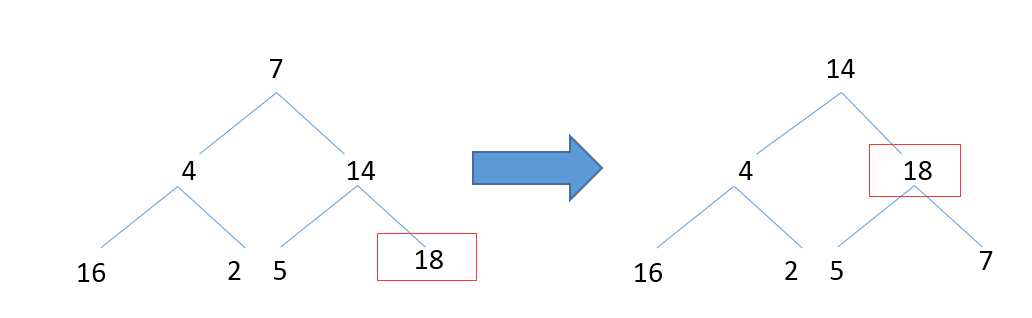
第一次max-heapify后，根节点并没有变成最大值，还要再遍历下根节点，这个显然在算法设计上不合适。所以自底向上的构思很巧妙。

HeapSort

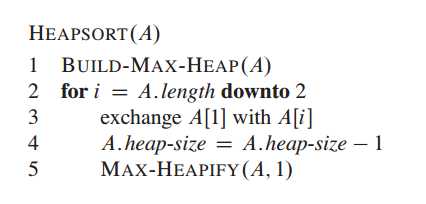
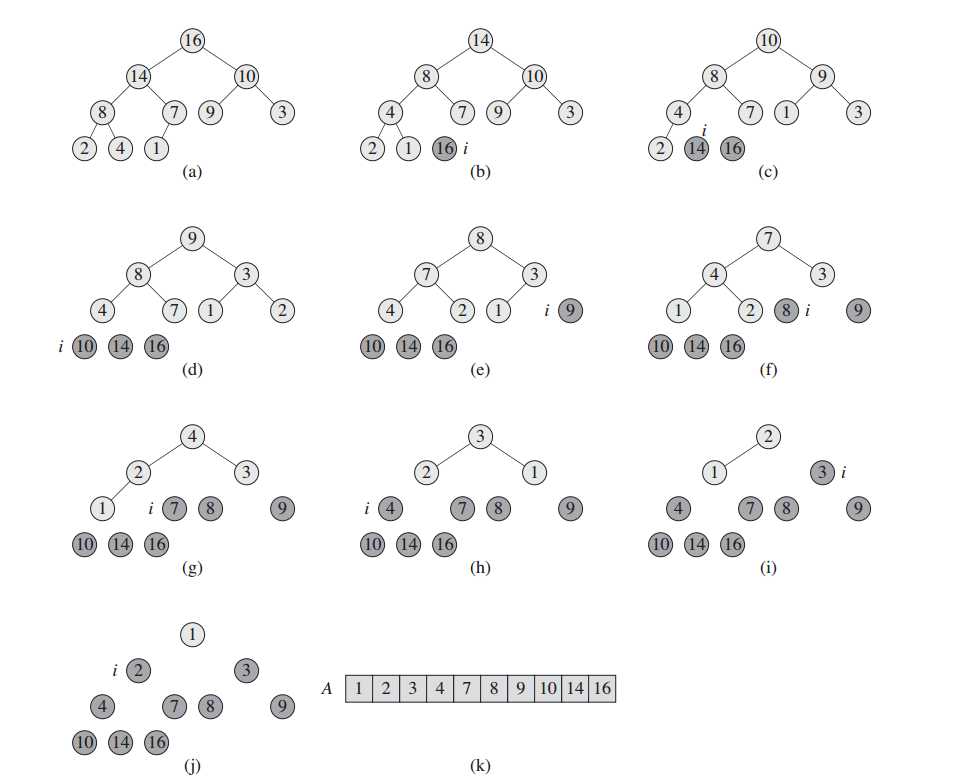
首先保证输出数据满足最大堆的数据属性（第一行），然后把最大值提取出来存储在数组末端；然后计算剩下数据的最大堆，把最大值提出来；循环操作到排序完成。采用算法导论图解

编程实现

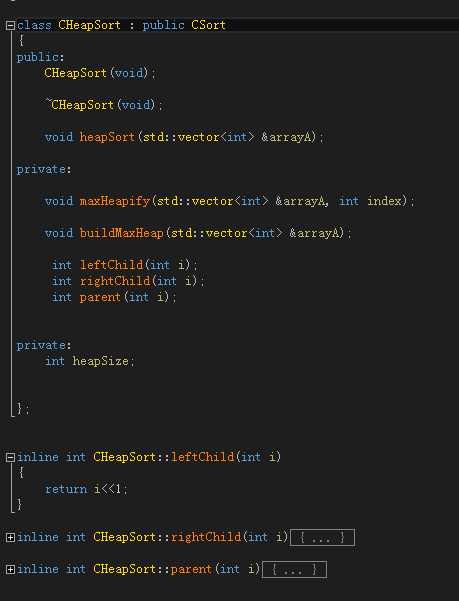
void CHeapSort::maxHeapify( std::vector<int> &arrayA, int index )
{

    
    int l = leftChild(index);
    int r = rightChild(index);

    int maxValue = 0;

    if(l < heapSize && arrayA[l] > arrayA[index])
    {
        maxValue = l;
    }
    else
    {
        maxValue = index;
    }

    if(r < heapSize && arrayA[r] > arrayA[maxValue])
    {
        maxValue = r;
    }

    /* 父节点部位最大值 */
    if(maxValue != index)
    {
        std::swap(arrayA[index],arrayA[maxValue]);
        maxHeapify(arrayA,maxValue);
    }


}

void CHeapSort::buildMaxHeap( std::vector<int> &arrayA )
{
    heapSize = arrayA.size();
    int halfSize = heapSize >> 1;

    for(int i = halfSize ;i >= 0; i--)
    {
        maxHeapify(arrayA,i);
    }
}

void CHeapSort::heapSort( std::vector<int> &arrayA )
{
    buildMaxHeap(arrayA);

    for(int i = arrayA.size() - 1; i > 0; i--)
    {
        std::swap(arrayA[0],arrayA[i]);
        heapSize--;
        maxHeapify(arrayA,0);
    }
}

 结果:

堆排序HeapSort

标签：vector   img   htc   大于等于   规律   数据结构堆   image   循环   没有   

原文地址：http://www.cnblogs.com/BellaVita/p/7831897.html