标签:closed 相同 alt 预测 算法 计算 range def 1.4
注:关于支持向量机系列文章是借鉴大神的神作,加以自己的理解写成的;若对原作者有损请告知,我会及时处理。转载请标明来源。
我在支持向量机系列中主要讲支持向量机的公式推导,第一部分讲到推出拉格朗日对偶函数的对偶因子α;第二部分是SMO算法对于对偶因子的求解;第三部分是核函数的原理与应用,讲核函数的推理及常用的核函数有哪些;第四部分是支持向量机的应用,按照机器学习实战的代码详细解读。
这篇文章是根据《机器学习实战》一书的实例进行代码的详细解读,我在查找这方面的资料没有人对支持向量机算法 python 实现的详细说明,我就把我在看代码时的思路和代码详细注解。如果存在不足,欢迎给我留言相互探讨。好了,废话不多说,正文开始。。。
首先我们使用的数据是二维的坐标点,还有对应的类标号(1 或 -1)。数据集以 “testSet.txt” 命名,如下代码段中:

1 3.542485 1.977398 -1 2 3.018896 2.556416 -1 3 7.551510 -1.580030 1 4 2.114999 -0.004466 -1 5 8.127113 1.274372 1 6 7.108772 -0.986906 1 7 8.610639 2.046708 1 8 2.326297 0.265213 -1 9 3.634009 1.730537 -1 10 0.341367 -0.894998 -1 11 3.125951 0.293251 -1 12 2.123252 -0.783563 -1 13 0.887835 -2.797792 -1 14 7.139979 -2.329896 1 15 1.696414 -1.212496 -1 16 8.117032 0.623493 1 17 8.497162 -0.266649 1 18 4.658191 3.507396 -1 19 8.197181 1.545132 1 20 1.208047 0.213100 -1 21 1.928486 -0.321870 -1 22 2.175808 -0.014527 -1 23 7.886608 0.461755 1 24 3.223038 -0.552392 -1 25 3.628502 2.190585 -1 26 7.407860 -0.121961 1 27 7.286357 0.251077 1 28 2.301095 -0.533988 -1 29 -0.232542 -0.547690 -1 30 3.457096 -0.082216 -1 31 3.023938 -0.057392 -1 32 8.015003 0.885325 1 33 8.991748 0.923154 1 34 7.916831 -1.781735 1 35 7.616862 -0.217958 1 36 2.450939 0.744967 -1 37 7.270337 -2.507834 1 38 1.749721 -0.961902 -1 39 1.803111 -0.176349 -1 40 8.804461 3.044301 1 41 1.231257 -0.568573 -1 42 2.074915 1.410550 -1 43 -0.743036 -1.736103 -1 44 3.536555 3.964960 -1 45 8.410143 0.025606 1 46 7.382988 -0.478764 1 47 6.960661 -0.245353 1 48 8.234460 0.701868 1 49 8.168618 -0.903835 1 50 1.534187 -0.622492 -1 51 9.229518 2.066088 1 52 7.886242 0.191813 1 53 2.893743 -1.643468 -1 54 1.870457 -1.040420 -1 55 5.286862 -2.358286 1 56 6.080573 0.418886 1 57 2.544314 1.714165 -1 58 6.016004 -3.753712 1 59 0.926310 -0.564359 -1 60 0.870296 -0.109952 -1 61 2.369345 1.375695 -1 62 1.363782 -0.254082 -1 63 7.279460 -0.189572 1 64 1.896005 0.515080 -1 65 8.102154 -0.603875 1 66 2.529893 0.662657 -1 67 1.963874 -0.365233 -1 68 8.132048 0.785914 1 69 8.245938 0.372366 1 70 6.543888 0.433164 1 71 -0.236713 -5.766721 -1 72 8.112593 0.295839 1 73 9.803425 1.495167 1 74 1.497407 -0.552916 -1 75 1.336267 -1.632889 -1 76 9.205805 -0.586480 1 77 1.966279 -1.840439 -1 78 8.398012 1.584918 1 79 7.239953 -1.764292 1 80 7.556201 0.241185 1 81 9.015509 0.345019 1 82 8.266085 -0.230977 1 83 8.545620 2.788799 1 84 9.295969 1.346332 1 85 2.404234 0.570278 -1 86 2.037772 0.021919 -1 87 1.727631 -0.453143 -1 88 1.979395 -0.050773 -1 89 8.092288 -1.372433 1 90 1.667645 0.239204 -1 91 9.854303 1.365116 1 92 7.921057 -1.327587 1 93 8.500757 1.492372 1 94 1.339746 -0.291183 -1 95 3.107511 0.758367 -1 96 2.609525 0.902979 -1 97 3.263585 1.367898 -1 98 2.912122 -0.202359 -1 99 1.731786 0.589096 -1 100 2.387003 1.573131 -1
然后,数据集中对象在下图显示,我们的工作就是找到最佳的超平面(这里是直线)。
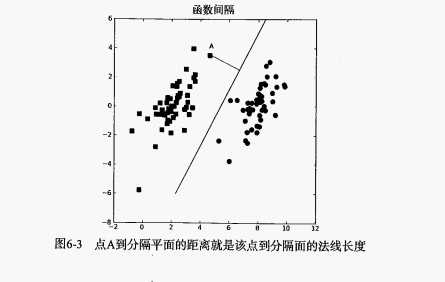
既然我们有了数据,那么就要把数据转换成可以被程序调用和处理的形式。写一个加载数据的函数,把文本中的数据转化成列表类型。代码如下:
1 # 将文本中的样本数据添加到列表中 2 def loadDataSet(fileName): 3 dataMat = [] 4 labelMat = [] 5 fr = open(fileName) 6 for line in fr.readlines() : # 对文本按行遍历 7 lineArr = line.strip().split(‘\t‘) 8 dataMat .append([float(lineArr [0]), float(lineArr[1])]) # 每行前两个是属性数据,最后一个是类标号 9 labelMat .append(float(lineArr[2])) 10 return dataMat , labelMat
由于在实现支持向量机的过程中要多次调用样本数据、类标号、对偶因子、对象经过核函数映射之后的值和其他数据,因此利用创造一个类,初始化这些数据利于保存和调用。代码如下:
1 class optStruct: 2 def __init__(self,dataMatIn, classLabels, C, toler, kTup): 3 self.X = dataMatIn # 样本数据 4 self.labelMat = classLabels # 样本的类标号 5 self.C = C # 对偶因子的上界值 6 self.tol = toler 7 self.m = shape(dataMatIn)[0] # 样本的行数,即样本对象的个数 8 self.alphas = mat(zeros((self.m, 1))) # 对偶因子 9 self.b = 0 # 分割函数的截距 10 self.eCache = mat(zeros((self.m, 2))) # 差值矩阵 m * 2,第一列是对象的标志位 1 表示存在不为零的差值 0 表示差值为零,第二列是实际的差值 E 11 self.K = mat(zeros((self.m, self.m))) # 对象经过核函数映射之后的值 12 for i in range(self.m): # 遍历全部样本集 13 self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup ) # 调用径向基核函数
我们通过支持向量机(二):SMO算法,可知对偶因子是我们求得超平面的关键,只有解得对偶因子才能得到超平面的法向量和截距。代码如下:
1 # 遍历所有能优化的 alpha 2 def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=(‘lin‘, 0)): 3 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup) # 创建一个类对象 oS ,类对象 oS 存放所有数据 4 iter = 0 # 迭代次数的初始化 5 entireSet = True # 违反 KKT 条件的标志符 6 alphaPairsChanged = 0 # 迭代中优化的次数 7 8 # 从选择第一个 alpha 开始,优化所有alpha 9 while(iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet )): # 优化的终止条件:在规定迭代次数下,是否遍历了整个样本或 alpha 是否优化 10 alphaPairsChanged = 0 11 if entireSet: # 12 for i in range(oS.m): # 遍历所有对象 13 alphaPairsChanged += innerL(i ,oS) # 调用优化函数(不一定优化) 14 print "fullSet , iter: %d i %d, pairs changed %d" % (iter, i , alphaPairsChanged ) 15 iter += 1 # 迭代次数加 1 16 else: 17 nonBoundIs = nonzero((oS.alphas .A > 0) * (oS.alphas.A < C))[0] 18 for i in nonBoundIs : # 遍历所有非边界样本集 19 alphaPairsChanged += innerL(i, oS) # 调用优化函数(不一定优化) 20 print "non-bound, iter: %d i :%d, pairs changed %d" % (iter, i, alphaPairsChanged ) 21 iter += 1 # 迭代次数加 1 22 if entireSet : # 没有违反KKT 条件的alpha ,终止迭代 23 entireSet = False 24 elif (alphaPairsChanged == 0): # 存在违反 KKT 的alpha 25 entireSet = True 26 print "iteration number: %d" % iter 27 return oS.b, oS.alphas # 返回截距值和 alphas
上述代码中,第 13 行调用了 innerL() 函数,它是对对偶因子向量的单个元素求解。代码如下:
1 # 优化选取两个 alpha ,并计算截距 b 2 def innerL(i, oS): 3 Ei = calcEk(oS, i) # 计算 对象 i 的差值 4 # 第一个 alpha 符合选择条件进入优化 5 if ((oS.labelMat [i]*Ei <- oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat [i]*Ei > oS.tol) and (oS.alphas[i] > 0)): 6 j,Ej =selectJ(i, oS, Ei) # 选择第二个 alpha 7 alphaIold = oS.alphas[i].copy() # 浅拷贝 8 alphaJold = oS.alphas[j].copy() # 浅拷贝 9 10 # 根据对象 i 、j 的类标号(相等或不等)确定KKT条件的上界和下界 11 if (oS.labelMat[i] != oS.labelMat[j]): 12 L = max(0, oS.alphas [j] - oS.alphas[i]) 13 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 14 else : 15 L = max(0, oS.alphas[j] + oS.alphas [i] - oS.C) 16 H = min(oS.C, oS.alphas [j] + oS.alphas [i]) 17 18 if L==H:print "L==H";return 0 # 不符合优化条件(第二个 alpha) 19 eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] # 计算公式的eta ,是公式的相反数 20 if eta >= 0:print "eta>=0";return 0 # 不考虑eta 大于等于 0 的情况(这种情况对 alpha 的解是另外一种方式,即临界情况的求解) 21 # 优化之后的第二个 alpha 值 22 oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 23 oS.alphas[j] = clipAlpha(oS.alphas[j], H, L) 24 updateEk(oS, j) # 更新差值矩阵 25 if (abs(oS.alphas[j] - alphaJold) < 0.00001): # 优化之后的 alpha 值与之前的值改变量太小,步长不足 26 print "j not moving enough" 27 return 0 28 oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j]) # 优化第二个 alpha 29 updateEk(oS, i) # 更新差值矩阵 30 # 计算截距 b 31 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i, j] 32 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j] 33 if (0 < oS.alphas [i]) and (oS.C > oS.alphas[i]): 34 oS.b = b1 35 elif (0 < oS.alphas [j]) and (oS.C > oS.alphas [j]): 36 oS.b = b2 37 else : 38 oS.b = (b1 + b2)/2.0 39 return 1 # 进行一次优化 40 else : 41 return 0
这里第 3 行代码调用了calcEk() 函数,它是计算预测值与真实值的差值。代码如下:
1 # 预测的类标号值与真实值的差值,参数 oS 是类对象,k 是样本的对象的标号 2 def calcEk(oS, k): 3 fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b) # 公式(1) 4 Ek = fXk - float(oS.labelMat[k]) # 差值 5 return Ek
其中,第 3 行中指到的公式(1)是超平面方程。
在 innerL()函数中的第 6 行,调用了 selectJ ()函数,此函数是用来选择优化的第二个对偶因子元素。代码如下:
1 # 由启发式选取第二个 alpha,以最大步长为标准 2 def selectJ(i, oS, Ei): # 函数的参数是选取的第一个 alpha 的对象号、类对象和对象差值 3 maxK = -1; maxDeltaE = 0; Ej = 0 # 第二个 alpha 的初始化 4 oS.eCache[i] = [1,Ei] # 更新差值矩阵的第 i 行 5 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # 取差值矩阵中第一列不为 0 的所有行数(标志位为 1 ),以元组类型返回 6 if (len(validEcacheList)) > 1 : # 7 for k in validEcacheList : # 遍历所有标志位为 1 的对象的差值 8 if k == i: continue 9 Ek = calcEk(oS, k) # 计算对象 k 的差值 10 deltaE = abs(Ei - Ek) # 取两个差值之差的绝对值 11 if (deltaE > maxDeltaE): # 选取最大的绝对值deltaE 12 maxK = k; maxDeltaE = deltaE; Ej = Ek 13 return maxK, Ej # 返回选取的第二个 alpha 14 else: # 随机选取第二个 alpha 15 j = selectJrand(i, oS.m) 16 Ej = calcEk(oS,j) 17 return j, Ej # 返回选取的第二个 alpha
这个函数的第 15 行调用了 selectJrand() 函数,是为了没有合适的第二个元素,就用随机的方式选择。代码如下:
1 # 随机选取对偶因子alpha ,参数i 是alpha 的下标,m 是alpha 的总数 2 def selectJrand(i,m): 3 j = i 4 while (j==i): 5 j = int(random.uniform(0,m)) 6 return j
在innerL()函数中的第 23 行调用 clipAlpha() 函数,是根据KKT 条件对对偶因子的修剪。代码如下:
1 # 对所求的对偶因子按约束条件的修剪 2 def clipAlpha(aj, H, L): # H 为上界,L为下界 3 if aj > H: 4 aj = H 5 if L > aj: 6 aj = L 7 return aj
innerL() 函数的第 29 行调用了 updateEk() 函数,更新差值矩阵的数据。代码如下:
1 # 更新差值矩阵的数据 2 def updateEk(oS, k): 3 Ek = calcEk(oS, k) # 调用计算差值的函数 4 oS.eCache [k] = [1,Ek]
这里我们使用的径向基核函数,把数据从低维映射到高维,把不可分数据变成可分。当然,我们给出的数据集是线性可分,现在给出另外数据集,分为训练集“testSetRBF.txt”和测试集"testSetRBF2.txt"。
径向基核函数公式如下:
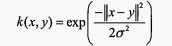
数据集

1 -0.214824 0.662756 -1.000000 2 -0.061569 -0.091875 1.000000 3 0.406933 0.648055 -1.000000 4 0.223650 0.130142 1.000000 5 0.231317 0.766906 -1.000000 6 -0.748800 -0.531637 -1.000000 7 -0.557789 0.375797 -1.000000 8 0.207123 -0.019463 1.000000 9 0.286462 0.719470 -1.000000 10 0.195300 -0.179039 1.000000 11 -0.152696 -0.153030 1.000000 12 0.384471 0.653336 -1.000000 13 -0.117280 -0.153217 1.000000 14 -0.238076 0.000583 1.000000 15 -0.413576 0.145681 1.000000 16 0.490767 -0.680029 -1.000000 17 0.199894 -0.199381 1.000000 18 -0.356048 0.537960 -1.000000 19 -0.392868 -0.125261 1.000000 20 0.353588 -0.070617 1.000000 21 0.020984 0.925720 -1.000000 22 -0.475167 -0.346247 -1.000000 23 0.074952 0.042783 1.000000 24 0.394164 -0.058217 1.000000 25 0.663418 0.436525 -1.000000 26 0.402158 0.577744 -1.000000 27 -0.449349 -0.038074 1.000000 28 0.619080 -0.088188 -1.000000 29 0.268066 -0.071621 1.000000 30 -0.015165 0.359326 1.000000 31 0.539368 -0.374972 -1.000000 32 -0.319153 0.629673 -1.000000 33 0.694424 0.641180 -1.000000 34 0.079522 0.193198 1.000000 35 0.253289 -0.285861 1.000000 36 -0.035558 -0.010086 1.000000 37 -0.403483 0.474466 -1.000000 38 -0.034312 0.995685 -1.000000 39 -0.590657 0.438051 -1.000000 40 -0.098871 -0.023953 1.000000 41 -0.250001 0.141621 1.000000 42 -0.012998 0.525985 -1.000000 43 0.153738 0.491531 -1.000000 44 0.388215 -0.656567 -1.000000 45 0.049008 0.013499 1.000000 46 0.068286 0.392741 1.000000 47 0.747800 -0.066630 -1.000000 48 0.004621 -0.042932 1.000000 49 -0.701600 0.190983 -1.000000 50 0.055413 -0.024380 1.000000 51 0.035398 -0.333682 1.000000 52 0.211795 0.024689 1.000000 53 -0.045677 0.172907 1.000000 54 0.595222 0.209570 -1.000000 55 0.229465 0.250409 1.000000 56 -0.089293 0.068198 1.000000 57 0.384300 -0.176570 1.000000 58 0.834912 -0.110321 -1.000000 59 -0.307768 0.503038 -1.000000 60 -0.777063 -0.348066 -1.000000 61 0.017390 0.152441 1.000000 62 -0.293382 -0.139778 1.000000 63 -0.203272 0.286855 1.000000 64 0.957812 -0.152444 -1.000000 65 0.004609 -0.070617 1.000000 66 -0.755431 0.096711 -1.000000 67 -0.526487 0.547282 -1.000000 68 -0.246873 0.833713 -1.000000 69 0.185639 -0.066162 1.000000 70 0.851934 0.456603 -1.000000 71 -0.827912 0.117122 -1.000000 72 0.233512 -0.106274 1.000000 73 0.583671 -0.709033 -1.000000 74 -0.487023 0.625140 -1.000000 75 -0.448939 0.176725 1.000000 76 0.155907 -0.166371 1.000000 77 0.334204 0.381237 -1.000000 78 0.081536 -0.106212 1.000000 79 0.227222 0.527437 -1.000000 80 0.759290 0.330720 -1.000000 81 0.204177 -0.023516 1.000000 82 0.577939 0.403784 -1.000000 83 -0.568534 0.442948 -1.000000 84 -0.011520 0.021165 1.000000 85 0.875720 0.422476 -1.000000 86 0.297885 -0.632874 -1.000000 87 -0.015821 0.031226 1.000000 88 0.541359 -0.205969 -1.000000 89 -0.689946 -0.508674 -1.000000 90 -0.343049 0.841653 -1.000000 91 0.523902 -0.436156 -1.000000 92 0.249281 -0.711840 -1.000000 93 0.193449 0.574598 -1.000000 94 -0.257542 -0.753885 -1.000000 95 -0.021605 0.158080 1.000000 96 0.601559 -0.727041 -1.000000 97 -0.791603 0.095651 -1.000000 98 -0.908298 -0.053376 -1.000000 99 0.122020 0.850966 -1.000000 100 -0.725568 -0.292022 -1.000000

1 0.676771 -0.486687 -1.000000 2 0.008473 0.186070 1.000000 3 -0.727789 0.594062 -1.000000 4 0.112367 0.287852 1.000000 5 0.383633 -0.038068 1.000000 6 -0.927138 -0.032633 -1.000000 7 -0.842803 -0.423115 -1.000000 8 -0.003677 -0.367338 1.000000 9 0.443211 -0.698469 -1.000000 10 -0.473835 0.005233 1.000000 11 0.616741 0.590841 -1.000000 12 0.557463 -0.373461 -1.000000 13 -0.498535 -0.223231 -1.000000 14 -0.246744 0.276413 1.000000 15 -0.761980 -0.244188 -1.000000 16 0.641594 -0.479861 -1.000000 17 -0.659140 0.529830 -1.000000 18 -0.054873 -0.238900 1.000000 19 -0.089644 -0.244683 1.000000 20 -0.431576 -0.481538 -1.000000 21 -0.099535 0.728679 -1.000000 22 -0.188428 0.156443 1.000000 23 0.267051 0.318101 1.000000 24 0.222114 -0.528887 -1.000000 25 0.030369 0.113317 1.000000 26 0.392321 0.026089 1.000000 27 0.298871 -0.915427 -1.000000 28 -0.034581 -0.133887 1.000000 29 0.405956 0.206980 1.000000 30 0.144902 -0.605762 -1.000000 31 0.274362 -0.401338 1.000000 32 0.397998 -0.780144 -1.000000 33 0.037863 0.155137 1.000000 34 -0.010363 -0.004170 1.000000 35 0.506519 0.486619 -1.000000 36 0.000082 -0.020625 1.000000 37 0.057761 -0.155140 1.000000 38 0.027748 -0.553763 -1.000000 39 -0.413363 -0.746830 -1.000000 40 0.081500 -0.014264 1.000000 41 0.047137 -0.491271 1.000000 42 -0.267459 0.024770 1.000000 43 -0.148288 -0.532471 -1.000000 44 -0.225559 -0.201622 1.000000 45 0.772360 -0.518986 -1.000000 46 -0.440670 0.688739 -1.000000 47 0.329064 -0.095349 1.000000 48 0.970170 -0.010671 -1.000000 49 -0.689447 -0.318722 -1.000000 50 -0.465493 -0.227468 -1.000000 51 -0.049370 0.405711 1.000000 52 -0.166117 0.274807 1.000000 53 0.054483 0.012643 1.000000 54 0.021389 0.076125 1.000000 55 -0.104404 -0.914042 -1.000000 56 0.294487 0.440886 -1.000000 57 0.107915 -0.493703 -1.000000 58 0.076311 0.438860 1.000000 59 0.370593 -0.728737 -1.000000 60 0.409890 0.306851 -1.000000 61 0.285445 0.474399 -1.000000 62 -0.870134 -0.161685 -1.000000 63 -0.654144 -0.675129 -1.000000 64 0.285278 -0.767310 -1.000000 65 0.049548 -0.000907 1.000000 66 0.030014 -0.093265 1.000000 67 -0.128859 0.278865 1.000000 68 0.307463 0.085667 1.000000 69 0.023440 0.298638 1.000000 70 0.053920 0.235344 1.000000 71 0.059675 0.533339 -1.000000 72 0.817125 0.016536 -1.000000 73 -0.108771 0.477254 1.000000 74 -0.118106 0.017284 1.000000 75 0.288339 0.195457 1.000000 76 0.567309 -0.200203 -1.000000 77 -0.202446 0.409387 1.000000 78 -0.330769 -0.240797 1.000000 79 -0.422377 0.480683 -1.000000 80 -0.295269 0.326017 1.000000 81 0.261132 0.046478 1.000000 82 -0.492244 -0.319998 -1.000000 83 -0.384419 0.099170 1.000000 84 0.101882 -0.781145 -1.000000 85 0.234592 -0.383446 1.000000 86 -0.020478 -0.901833 -1.000000 87 0.328449 0.186633 1.000000 88 -0.150059 -0.409158 1.000000 89 -0.155876 -0.843413 -1.000000 90 -0.098134 -0.136786 1.000000 91 0.110575 -0.197205 1.000000 92 0.219021 0.054347 1.000000 93 0.030152 0.251682 1.000000 94 0.033447 -0.122824 1.000000 95 -0.686225 -0.020779 -1.000000 96 -0.911211 -0.262011 -1.000000 97 0.572557 0.377526 -1.000000 98 -0.073647 -0.519163 -1.000000 99 -0.281830 -0.797236 -1.000000 100 -0.555263 0.126232 -1.000000
核函数代码如下:
1 # 径向基核函数(高斯函数) 2 def kernelTrans(X, A, kTup): # X 是样本集矩阵,A 是样本对象(矩阵的行向量) , kTup 元组 3 m,n = shape(X) 4 K = mat(zeros((m,1))) 5 # 数据不用核函数计算 6 if kTup [0] == ‘lin‘: K = X * A.T 7 8 # 用径向基核函数计算 9 elif kTup[0] == ‘rbf‘: 10 for j in range(m): 11 deltaRow = X[j,:] - A 12 K[j] = deltaRow * deltaRow.T 13 K = exp(K/(-1*kTup[1]**2)) 14 # kTup 元组值异常,抛出异常信息 15 else:raise NameError(‘Houston We Have a Problem --That Kernel is not recognized‘) 16 return K
测试函数代码如下:
1 # 训练样本集的错误率和测试样本集的错误率 2 def testRbf(k1=1.3): 3 dataArr,labelArr = loadDataSet(‘testSetRBF.txt‘) # 训练样本的提取 4 b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, (‘rbf‘, k1)) # 计算得到截距和对偶因子 5 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() 6 svInd=nonzero(alphas.A>0)[0] # 对偶因子大于零的值,支持向量的点对应对偶因子 7 sVs=datMat[svInd] 8 labelSV = labelMat[svInd] 9 print "there are %d Support Vectors" % shape(sVs)[0] 10 m,n = shape(datMat) 11 errorCount = 0 12 # 对训练样本集的测试 13 for i in range(m): 14 kernelEval = kernelTrans(sVs,datMat[i,:],(‘rbf‘, k1)) # 对象 i 的映射值 15 predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b # 预测值 16 if sign(predict)!=sign(labelArr[i]): errorCount += 1 17 print "the training error rate is: %f" % (float(errorCount)/m) 18 dataArr,labelArr = loadDataSet(‘testSetRBF2.txt‘) # 测试样本集的提取 19 errorCount = 0 20 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() 21 m,n = shape(datMat) 22 # 对测试样本集的测试 23 for i in range(m): 24 kernelEval = kernelTrans(sVs,datMat[i,:],(‘rbf‘, k1)) # 测试样本对象 i 的映射值 25 predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b # 预测值 26 if sign(predict)!=sign(labelArr[i]): errorCount += 1 27 print "the test error rate is: %f" % (float(errorCount)/m)
运行结果:
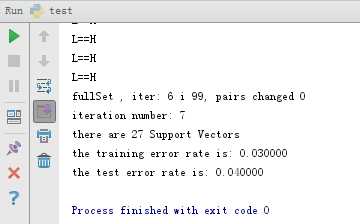
从结果可知,训练集的错误率在3%,测试集的错误率在4%,说明支持向量机的分类效果很好。当然在每次运行的结果与图中的结果不一定相同,因为代码段中存在随机选择对偶因子的情况,这是无法避免的,但结果的错误率是基本相同的。
到这里支持向量机算法是讲完了,期间花费了我大量时间学习支持向量机的原理和代码的实现。虽然这部分内容存在一定的难度,但认真地去看每步的由来还是能够理解的。像我这么不怎么聪明的人都能对它说出 1,2,3,4 来,相信你也可以。我总是这么认为,你看懂支持向量机是一回事,能够说出向量机是一回事,把向量机讲出来又是另外一回事。我现在对支持向量机还有很多半只不懂的地方,希望以后对它有了新的理解再来修改支持向量机系列的文章。

1 #-*- coding=utf-8 -*- 2 import random 3 4 from numpy import * 5 6 # 将文本中的样本数据添加到列表中 7 def loadDataSet(fileName): 8 dataMat = [] 9 labelMat = [] 10 fr = open(fileName) 11 for line in fr.readlines() : # 对文本按行遍历 12 lineArr = line.strip().split(‘\t‘) 13 dataMat .append([float(lineArr [0]), float(lineArr[1])]) # 每行前两个是属性数据,最后一个是类标号 14 labelMat .append(float(lineArr[2])) 15 return dataMat , labelMat 16 17 # 随机选取对偶因子alpha ,参数i 是alpha 的下标,m 是alpha 的总数 18 def selectJrand(i,m): 19 j = i 20 while (j==i): 21 j = int(random.uniform(0,m)) 22 return j 23 24 # 对所求的对偶因子按约束条件的修剪 25 def clipAlpha(aj, H, L): # H 为上界,L为下界 26 if aj > H: 27 aj = H 28 if L > aj: 29 aj = L 30 return aj 31 32 33 class optStruct: 34 def __init__(self,dataMatIn, classLabels, C, toler, kTup): 35 self.X = dataMatIn # 样本数据 36 self.labelMat = classLabels # 样本的类标号 37 self.C = C # 对偶因子的上界值 38 self.tol = toler 39 self.m = shape(dataMatIn)[0] # 样本的行数,即样本对象的个数 40 self.alphas = mat(zeros((self.m, 1))) # 对偶因子 41 self.b = 0 # 分割函数的截距 42 self.eCache = mat(zeros((self.m, 2))) # 差值矩阵 m * 2,第一列是对象的标志位 1 表示存在不为零的差值 0 表示差值为零,第二列是实际的差值 E 43 self.K = mat(zeros((self.m, self.m))) # 对象经过核函数映射之后的值 44 for i in range(self.m): # 遍历全部样本集 45 self.K[:,i] = kernelTrans(self.X, self.X[i,:], kTup ) # 调用径向基核函数 46 47 48 49 # 预测的类标号值与真实值的差值,参数 oS 是类对象,k 是样本的对象的标号 50 def calcEk(oS, k): 51 fXk = float(multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b) # 公式(1) 52 Ek = fXk - float(oS.labelMat[k]) # 差值 53 return Ek 54 55 56 # 由启发式选取第二个 alpha,以最大步长为标准 57 def selectJ(i, oS, Ei): # 函数的参数是选取的第一个 alpha 的对象号、类对象和对象差值 58 maxK = -1; maxDeltaE = 0; Ej = 0 # 第二个 alpha 的初始化 59 oS.eCache[i] = [1,Ei] # 更新差值矩阵的第 i 行 60 validEcacheList = nonzero(oS.eCache[:,0].A)[0] # 取差值矩阵中第一列不为 0 的所有行数(标志位为 1 ),以元组类型返回 61 if (len(validEcacheList)) > 1 : # 62 for k in validEcacheList : # 遍历所有标志位为 1 的对象的差值 63 if k == i: continue 64 Ek = calcEk(oS, k) # 计算对象 k 的差值 65 deltaE = abs(Ei - Ek) # 取两个差值之差的绝对值 66 if (deltaE > maxDeltaE): # 选取最大的绝对值deltaE 67 maxK = k; maxDeltaE = deltaE; Ej = Ek 68 return maxK, Ej # 返回选取的第二个 alpha 69 else: # 随机选取第二个 alpha 70 j = selectJrand(i, oS.m) 71 Ej = calcEk(oS,j) 72 return j, Ej # 返回选取的第二个 alpha 73 74 # 更新差值矩阵的数据 75 def updateEk(oS, k): 76 Ek = calcEk(oS, k) # 调用计算差值的函数 77 oS.eCache [k] = [1,Ek] 78 79 80 # 优化选取两个 alpha ,并计算截距 b 81 def innerL(i, oS): 82 Ei = calcEk(oS, i) # 计算 对象 i 的差值 83 # 第一个 alpha 符合选择条件进入优化 84 if ((oS.labelMat [i]*Ei <- oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat [i]*Ei > oS.tol) and (oS.alphas[i] > 0)): 85 j,Ej =selectJ(i, oS, Ei) # 选择第二个 alpha 86 alphaIold = oS.alphas[i].copy() # 浅拷贝 87 alphaJold = oS.alphas[j].copy() # 浅拷贝 88 89 # 根据对象 i 、j 的类标号(相等或不等)确定KKT条件的上界和下界 90 if (oS.labelMat[i] != oS.labelMat[j]): 91 L = max(0, oS.alphas [j] - oS.alphas[i]) 92 H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i]) 93 else : 94 L = max(0, oS.alphas[j] + oS.alphas [i] - oS.C) 95 H = min(oS.C, oS.alphas [j] + oS.alphas [i]) 96 97 if L==H:print "L==H";return 0 # 不符合优化条件(第二个 alpha) 98 eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] # 计算公式的eta ,是公式的相反数 99 if eta >= 0:print "eta>=0";return 0 # 不考虑eta 大于等于 0 的情况(这种情况对 alpha 的解是另外一种方式,即临界情况的求解) 100 # 优化之后的第二个 alpha 值 101 oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta 102 oS.alphas[j] = clipAlpha(oS.alphas[j], H, L) 103 updateEk(oS, j) # 更新差值矩阵 104 if (abs(oS.alphas[j] - alphaJold) < 0.00001): # 优化之后的 alpha 值与之前的值改变量太小,步长不足 105 print "j not moving enough" 106 return 0 107 oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j]) # 优化第二个 alpha 108 updateEk(oS, i) # 更新差值矩阵 109 # 计算截距 b 110 b1 = oS.b - Ei - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, i] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[i, j] 111 b2 = oS.b - Ej - oS.labelMat[i] * (oS.alphas[i] - alphaIold) * oS.K[i, j] - oS.labelMat[j] * (oS.alphas[j] - alphaJold) * oS.K[j, j] 112 if (0 < oS.alphas [i]) and (oS.C > oS.alphas[i]): 113 oS.b = b1 114 elif (0 < oS.alphas [j]) and (oS.C > oS.alphas [j]): 115 oS.b = b2 116 else : 117 oS.b = (b1 + b2)/2.0 118 return 1 # 进行一次优化 119 else : 120 return 0 121 122 123 # 遍历所有能优化的 alpha 124 def smoP(dataMatIn, classLabels, C, toler, maxIter, kTup=(‘lin‘, 0)): 125 oS = optStruct(mat(dataMatIn), mat(classLabels).transpose(), C, toler, kTup) # 创建一个类对象 oS ,类对象 oS 存放所有数据 126 iter = 0 # 迭代次数的初始化 127 entireSet = True # 违反 KKT 条件的标志符 128 alphaPairsChanged = 0 # 迭代中优化的次数 129 130 # 从选择第一个 alpha 开始,优化所有alpha 131 while(iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet )): # 优化的终止条件:在规定迭代次数下,是否遍历了整个样本或 alpha 是否优化 132 alphaPairsChanged = 0 133 if entireSet: # 134 for i in range(oS.m): # 遍历所有对象 135 alphaPairsChanged += innerL(i ,oS) # 调用优化函数(不一定优化) 136 print "fullSet , iter: %d i %d, pairs changed %d" % (iter, i , alphaPairsChanged ) 137 iter += 1 # 迭代次数加 1 138 else: 139 nonBoundIs = nonzero((oS.alphas .A > 0) * (oS.alphas.A < C))[0] 140 for i in nonBoundIs : # 遍历所有非边界样本集 141 alphaPairsChanged += innerL(i, oS) # 调用优化函数(不一定优化) 142 print "non-bound, iter: %d i :%d, pairs changed %d" % (iter, i, alphaPairsChanged ) 143 iter += 1 # 迭代次数加 1 144 if entireSet : # 没有违反KKT 条件的alpha ,终止迭代 145 entireSet = False 146 elif (alphaPairsChanged == 0): # 存在违反 KKT 的alpha 147 entireSet = True 148 print "iteration number: %d" % iter 149 return oS.b, oS.alphas # 返回截距值和 alphas 150 151 # 径向基核函数(高斯函数) 152 def kernelTrans(X, A, kTup): # X 是样本集矩阵,A 是样本对象(矩阵的行向量) , kTup 元组 153 m,n = shape(X) 154 K = mat(zeros((m,1))) 155 # 数据不用核函数计算 156 if kTup [0] == ‘lin‘: K = X * A.T 157 158 # 用径向基核函数计算 159 elif kTup[0] == ‘rbf‘: 160 for j in range(m): 161 deltaRow = X[j,:] - A 162 K[j] = deltaRow * deltaRow.T 163 K = exp(K/(-1*kTup[1]**2)) 164 # kTup 元组值异常,抛出异常信息 165 else:raise NameError(‘Houston We Have a Problem --That Kernel is not recognized‘) 166 return K 167 168 # 训练样本集的错误率和测试样本集的错误率 169 def testRbf(k1=1.3): 170 dataArr,labelArr = loadDataSet(‘testSetRBF.txt‘) # 训练样本的提取 171 b,alphas = smoP(dataArr, labelArr, 200, 0.0001, 10000, (‘rbf‘, k1)) # 计算得到截距和对偶因子 172 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() 173 svInd=nonzero(alphas.A>0)[0] # 对偶因子大于零的值,支持向量的点对应对偶因子 174 sVs=datMat[svInd] 175 labelSV = labelMat[svInd] 176 print "there are %d Support Vectors" % shape(sVs)[0] 177 m,n = shape(datMat) 178 errorCount = 0 179 # 对训练样本集的测试 180 for i in range(m): 181 kernelEval = kernelTrans(sVs,datMat[i,:],(‘rbf‘, k1)) # 对象 i 的映射值 182 predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b # 预测值 183 if sign(predict)!=sign(labelArr[i]): errorCount += 1 184 print "the training error rate is: %f" % (float(errorCount)/m) 185 dataArr,labelArr = loadDataSet(‘testSetRBF2.txt‘) # 测试样本集的提取 186 errorCount = 0 187 datMat=mat(dataArr); labelMat = mat(labelArr).transpose() 188 m,n = shape(datMat) 189 # 对测试样本集的测试 190 for i in range(m): 191 kernelEval = kernelTrans(sVs,datMat[i,:],(‘rbf‘, k1)) # 测试样本对象 i 的映射值 192 predict=kernelEval.T * multiply(labelSV,alphas[svInd]) + b # 预测值 193 if sign(predict)!=sign(labelArr[i]): errorCount += 1 194 print "the test error rate is: %f" % (float(errorCount)/m) 195 if __name__ == ‘__main__‘: 196 197 ‘‘‘ 198 # 显示计算的截距值b 和对偶因子 alphas 199 dataMat ,labelMat = loadDataSet(‘testSet.txt‘) 200 b, alphas = smoP(dataMat, labelMat , 0.6, 0.11, 40,(‘rbf‘,2)) 201 print ‘------‘ 202 print b, ‘----‘,alphas 203 ‘‘‘ 204 205 # 支持向量机的测试 206 testRbf()
机器学习之支持向量机(四):支持向量机的Python语言实现
标签:closed 相同 alt 预测 算法 计算 range def 1.4
原文地址:http://www.cnblogs.com/pursued-deer/p/7892342.html