标签:位运算 矩阵转置 类型 return tps 结构 顺序 code putchar

{
int n,j,i,k;
输入n;
/*输出上半部分*/
for (i=1;i<=n;i=i+2) { 输出上半个菱形
for(j=n-i;j>0;j--)每一行输出的空格比上一行少两个
printf(" ");
for(k=i;k>0;k--)每一行输出的* 等于行数
printf("* ") ;
putchar(‘\n‘);换行
}
/*输出下半部分*/
for(i=n-2;i>0;i=i-2) { 下半部分与上半部分相反
for(j=n-i;j>0;j--) 输出的空格数
printf(" ");
for(k=i;k>0;k--)每一行输出的* 等于行数
printf("* ") ;
putchar(‘\n‘);换行
}
return 0;
}
碰到的问题:输出空格时判断条件写成(j=n-i+1;j>0;j--),导致多输出一个空格
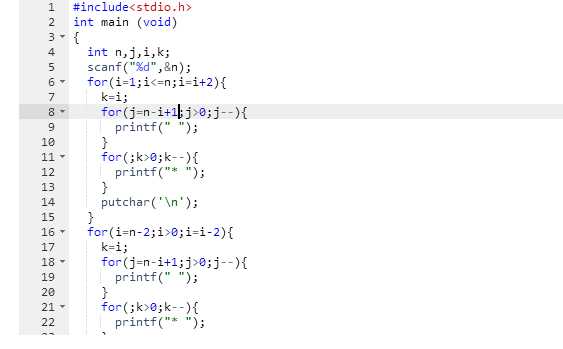
调试过程:输入3,输出空格后
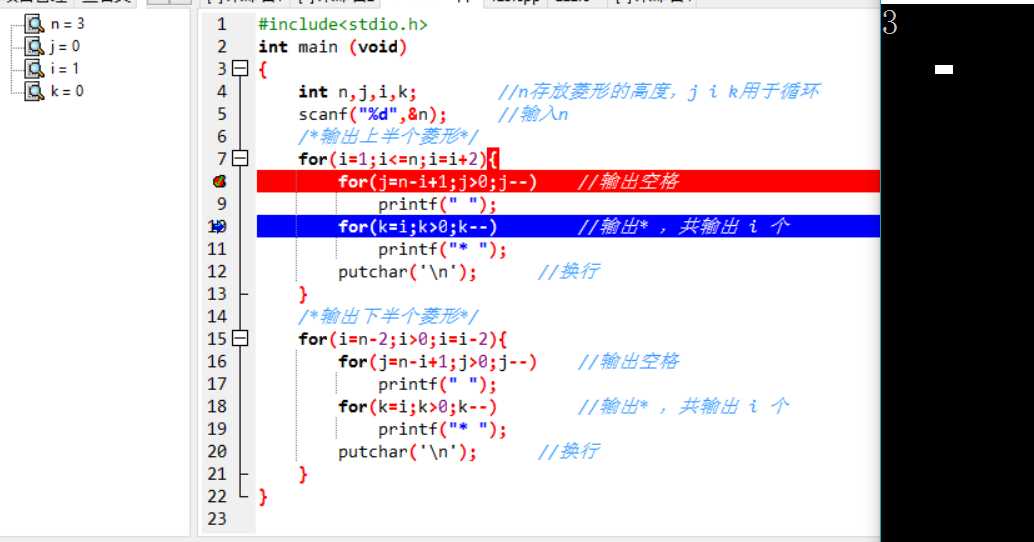
输出*

换行后,发现又输出了空格,n=3时,第二行应该没有空格
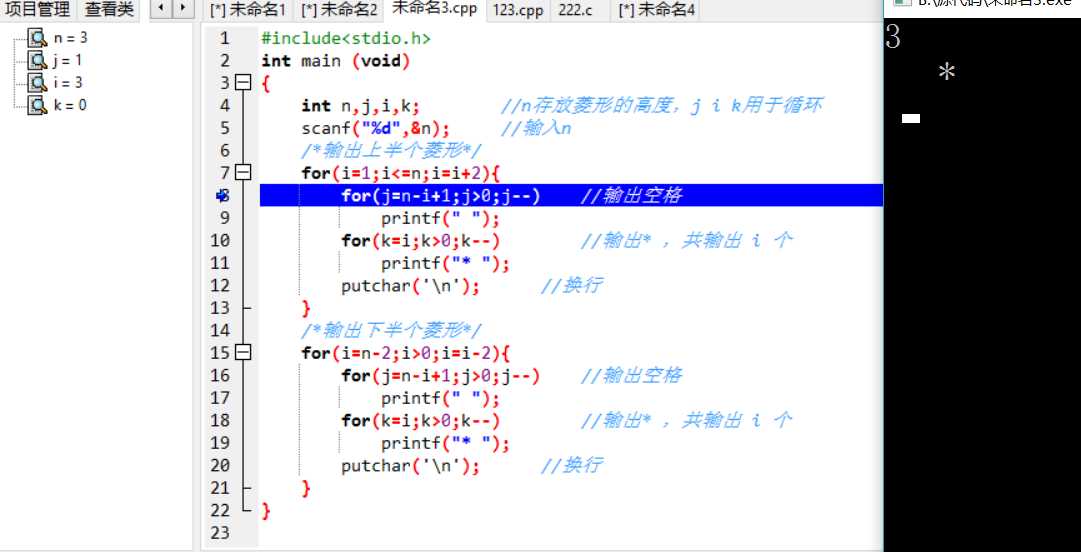
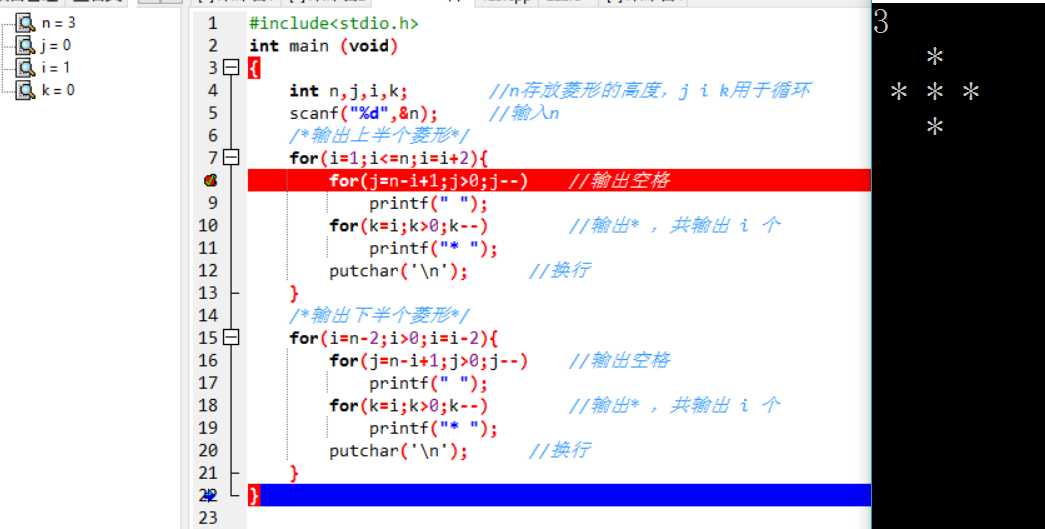

{
定义变量分别存放原来的数以及计算后的数,定义count=1表示计算的次数
输入第一个数num1
储存num1,令num2=num1
调用trap函数,传入num1并将返还值存于num1
if(num1==num2)
输出printf("%d:%d",count,num1);
else{
while(num1!=num2){
储存num1的值,num2=num1;
调用函数num1=trap(num1);
输出printf("%d:%d",count,num1);
count++;
}
循环结束再输出一次 printf("%d:%d",count,num1);
}
结束 ;
}
int trap(int n) 计算陷阱数函数
{
int x,sum=0;
while(x>0){
取出最低位x=n%10;
累加到 sum;
去掉最低位 x/=10;
}
sum = 3*sum+1;
返还函数值 ;
} 
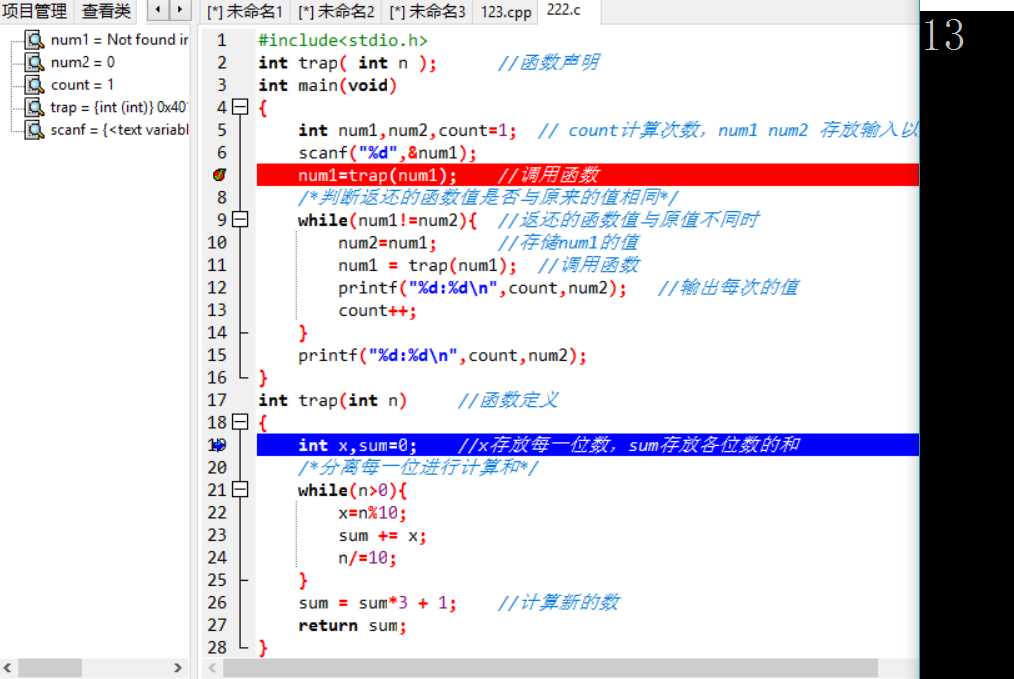
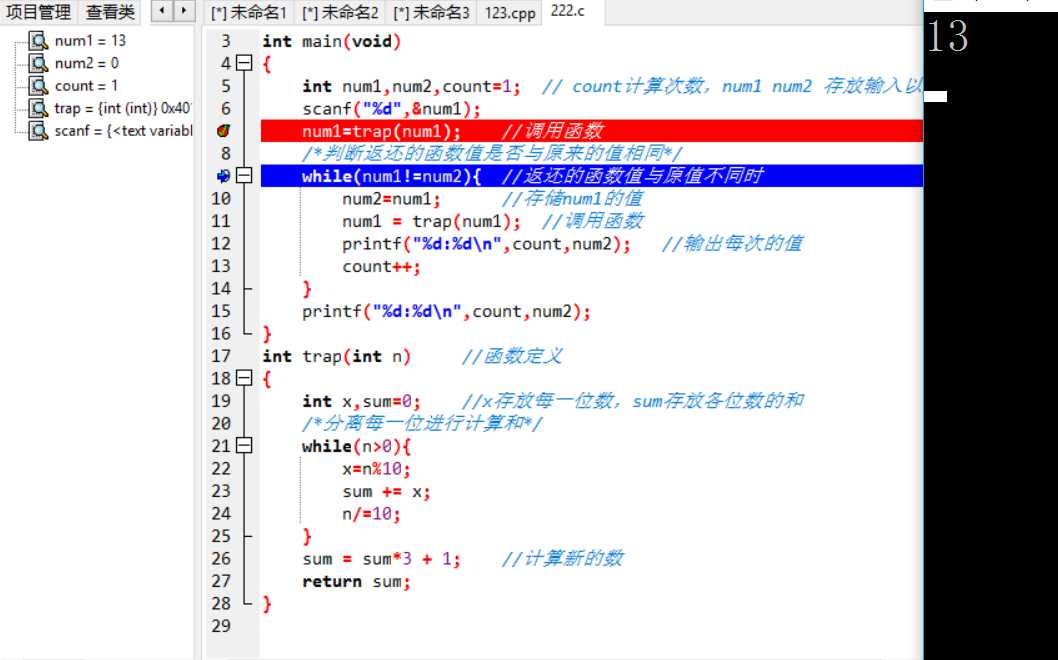
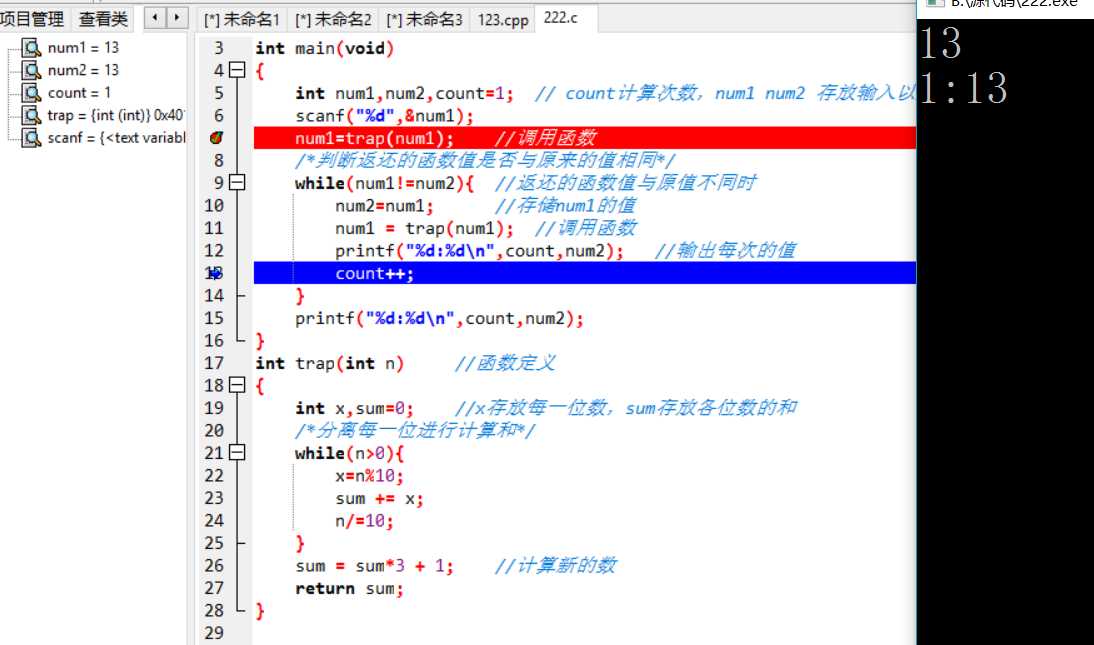
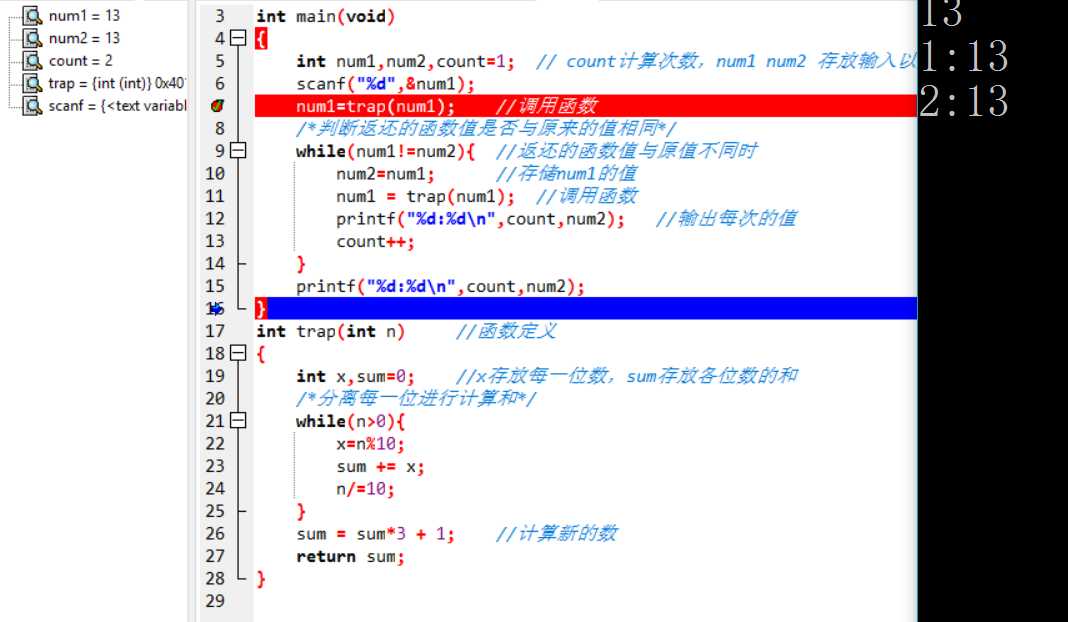
PTA列表说明:主要情况就是上述问题
{
定义变量 int num,sum;
char op;
输入第一个数字num和第一个运算符op;
赋值sum=num;
while op!=‘=‘{
输入数字num;
if (op==‘/‘&&num==0)||(op!=‘+‘&&op!=‘-‘&&op!=‘*‘&&op!=‘/‘&&op!=‘=‘){ //如果运算符为‘/’同时输入数为0或者运算符不为‘+’,‘-’,‘*’,‘/’
输出Error;
结束 return 0;
}
else{
switch(op){ //判断运算符并进行相应运算
case ‘+‘:sum+=num;break;
case ‘-‘:sum-=num;break;
case ‘/‘:sum/=num;break;
case ‘*‘:sum*=num;break;
}
输入下一个运算符 op;
}
}
输出结果sum;
结束 return 0;
} 
本题调试过程碰到的问题: (op==‘/‘&&num==0)的条件写成 (op=‘/‘&&num==0),少了一个等号导致判断条件错误

PTA提交列表说明
PTA2分的提交列表是因为op==‘/‘中少了一个等号,16分是因为没有对分母为0以及非法运算符进行判断

定义 : 类型名 变量名 [数组长度]
初始化:
通过循环结构实现,如:
int n[10];
for(i=0;i<10;i++){
scanf("%d",n[i]);
}
数组是把相同类型的一系列数据统一编制到某一个组别中,这样就可以通过数组名+索引号简单快捷的操作大量数据。
选择法:

冒泡法:
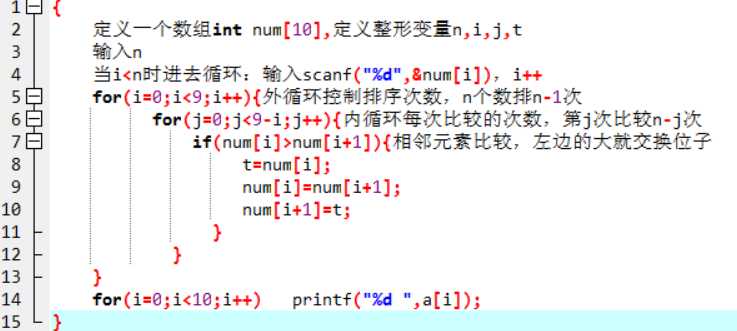
直接插入排序:

二分查找法:取中间元素与查找元素进行比较,如果查找元素比中间元素大,则在中间元素右边查找,如果查找元素比中间元素小,则在中间元素的左边查找。
与顺序查找法的区别:二分查找法的效率更高
二维数组定义:类型名 变量名 [行长度] [列长度]
初始化:
分行赋初值:
一般形式为: 类型名 变量名 [行长度] [列长度]{{初值表0},...{初值表k},...}
例如:int a[2][3] = {{1,2,3},{4,5.6}}
顺序赋初值:
一般形式为: 类型名 变量名 [行长度] [列长度]{ 初值表 }
例如:int [2][3]{1,2,3,4,5,6}

矩阵转置过程:对角线上元素不变,其余元素两个下标互换,如:n[0][1] 转置后变为 n[1][0]
下三角:i>=j
上三角:i<=j
对称矩阵:i=j
应用在数组为矩阵形式的时候
标签:位运算 矩阵转置 类型 return tps 结构 顺序 code putchar
原文地址:http://www.cnblogs.com/xzjj/p/7881776.html